Introducing Consistent Hashing

Hajautettujen arkkitehtuureiden yleistymisen myötä johdonmukaisesta hashinasta tuli valtavirtaa. Mutta mitä se tarkalleen ottaen on ja miten se eroaa tavallisesta hashausalgoritmista? Mitkä ovat sen tarkat motiivit?

Aluksi kuvataan tärkeimmät käsitteet. Sen jälkeen perehdymme olemassa oleviin algoritmeihin ymmärtääkseen johdonmukaiseen hashaukseen liittyviä haasteita.

Hashing

Hashing on prosessi, jossa mielivaltaisen kokoista dataa kuvataan kiinteän kokoisiin arvoihin. Jokaisella olemassa olevalla algoritmilla on oma spesifikaationsa:

• MD5 tuottaa 128-bittisiä hash-arvoja.
• SHA-1 tuottaa 160-bittisiä hash-arvoja.
• jne.

Hashingilla on monia sovelluksia tietotekniikassa. Esimerkiksi yksi näistä sovelluksista on nimeltään tarkistussumma. Tietoaineiston eheyden tarkistamiseen voidaan käyttää hashausalgoritmia. Palvelin hashaa tietokokonaisuuden ja ilmoittaa hash-arvon asiakkaalle. Tämän jälkeen asiakas hashaa oman versionsa tietokokonaisuudesta ja vertaa hash-arvoja. Jos ne ovat samat, eheys pitäisi varmistaa.

”pitäisi” on tässä tärkeä. Pahimmassa tapauksessa törmäys tapahtuu. Törmäys on se, kun kahdella eri datalla on sama hash-arvo. Otetaanpa käytännön esimerkki määrittelemällä seuraava hashausfunktio: kun annetaan henkilö, se palauttaa hänen syntymäpäivänsä (päivä & syntymäkuukausi). Syntymäpäiväparadoksi kertoo, että jos huoneessa on vain 23 henkilöä, todennäköisyys sille, että kahdella henkilöllä on sama syntymäpäivä (eli törmäys), on yli 50 %. Siksi syntymäpäiväfunktio ei todennäköisesti ole hyvä hashifunktio.

Nopeana johdantona hashifiointiin on tärkeää ymmärtää, että pääidea on arvojen hajauttaminen tietylle alueelle. Esimerkiksi:

• MD5 levittää arvot 128-bittiseen avaruusalueeseen
• Hashtable (tai hashmap), jonka tukena on 32-alkioinen array, on sisäinen hashing-funktio, joka levittää arvot mihin tahansa indeksiin (0:sta 31:een).

Kuormituksen jakaminen

Kuormituksen jakaminen voidaan määritellä kuormituksen levittämiseksi solmupisteiden kesken. Termi solmu on tässä yhteydessä vaihdettavissa palvelimen tai instanssin kanssa. Se on laskentayksikkö.

Kuormituksen tasaus on yksi esimerkki kuormituksen jakamisesta. Siinä on kyse joukon tehtävien jakamisesta resurssien kesken. Kuormantasausta käytetään esimerkiksi API-pyyntöjen jakamiseen web-palvelininstanssien kesken.

Kun on kyse datasta, käytetään mieluummin termiä sharding. Tietokannan shard on tietokannan datan horisontaalinen osio. Tyypillinen esimerkki on tietokanta, joka on jaettu kolmeen shardiin, joissa kussakin shardissa on osajoukko koko datasta.

Kuormituksen tasaamisella ja shardoinnilla on joitakin yhteisiä haasteita. Datan jakaminen tasaisesti esimerkiksi sen takaamiseksi, että jokin solmu ei ole ylikuormittunut muihin verrattuna. Joissain yhteyksissä kuormantasauksen ja shardauksen on myös jatkuvasti yhdistettävä tehtäviä tai dataa samaan solmuun:

• Jos meidän on serialisoitava, käsiteltävä yksi kerrallaan, tietyn kuluttajan operaatiot, meidän on reititettävä pyyntö samaan solmuun.
• Jos meidän on jaettava dataa, meidän on tiedettävä, mikä shard on tietyn avaimen omistaja.

Kuulostaako tutulta? Näissä kahdessa esimerkissä levitämme arvoja toimialueelle. Olipa kyseessä sitten palvelinsolmuihin levitettävä tehtävä tai tietokannan shardiin levitettävä data, löydämme takaisin hashingiin liittyvän ajatuksen. Tästä syystä hashingia voidaan käyttää yhdessä kuormanjaon kanssa. Katsotaanpa miten.

Mod-n-hashing

Mod-n-hashingin periaate on seuraava. Jokainen avain hashataan käyttämällä hashausfunktiota, joka muuttaa syötteen kokonaisluvuksi. Sitten suoritetaan solmujen lukumäärään perustuva modulo.

Katsotaanpa konkreettinen esimerkki, jossa on 3 solmua. Tässä meidän on jaettava kuorma näiden solmujen kesken avaintunnisteen perusteella. Jokainen avain hashataan, minkä jälkeen suoritetaan modulo-operaatio:

Tämän lähestymistavan etuna on sen tilattomuus. Meidän ei tarvitse säilyttää mitään tilaa muistuttamassa meitä siitä, että foo ohjattiin solmuun 2. Silti meidän on tiedettävä, kuinka monta solmua on konfiguroitu modulo-operaation soveltamiseksi.

Miten mekanismi sitten toimii, jos se skaalautuu ulos- tai sisäänpäin (solmuja lisätään tai poistetaan)? Jos lisäämme toisen solmun, modulo-operaatio perustuu nyt 3:n sijasta 4:ään:

Kuten huomaamme, avaimia foo ja baz ei enää liitetä samaan solmuun. Mod-n-hashaussa ei ole mitään takeita siitä, että avaimen ja solmun välinen yhteys säilyy johdonmukaisena. Onko tämä ongelma? Saattaa olla.

Mitä jos toteutamme tietovaraston käyttäen shardingia ja perustuen mod-n-strategiaan tietojen jakamiseen? Jos skaalaamme solmujen määrää, meidän on suoritettava tasapainotusoperaatio. Edellisessä esimerkissä uudelleentasapainotus tarkoittaa:

• Siirretään foo solmusta 2 solmuun 0.
• Siirretään baz solmusta 2 solmuun 3.

Mutta mitä tapahtuu, jos olisimme tallentaneet miljoonia tai jopa miljardeja tietoja ja meidän pitäisi tasapainottaa melkein kaikki uudelleen? Kuten voimme kuvitella, tämä olisi raskas prosessi. Siksi meidän on muutettava kuormanjakotekniikkaamme varmistaaksemme, että uudelleentasapainotuksen yhteydessä:

• Jakauma pysyy mahdollisimman tasaisena solmujen uuden lukumäärän perusteella.
• Migroitavien avainten lukumäärän tulisi olla rajoitettu. Ihannetapauksessa se olisi vain 1/n prosenttia avaimista, missä n on solmujen lukumäärä.

Juuri tämä on johdonmukaisten hashausalgoritmien tarkoitus.

Termi johdonmukainen saattaa tosin olla hieman sekava. Tapasin insinöörejä, jotka olettivat, että tällaiset algoritmit yhdistävät tietyn avaimen aina samaan solmuun jopa skaalautuvuudesta huolimatta. Näin ei kuitenkaan ole. Sen täytyy olla johdonmukainen tiettyyn pisteeseen asti, jotta jakauma pysyy tasaisena.

Nyt on aika kaivaa joitakin ratkaisuja.

Rendezvous

Rendezvous oli ensimmäinen algoritmi, jota koskaan ehdotettiin ongelmamme ratkaisemiseksi. Vaikka alkuperäisessä, vuonna 1996 julkaistussa tutkimuksessa ei mainita termiä consistent hashing, se tarjoaa ratkaisun kuvaamiimme haasteisiin. Katsotaanpa yksi mahdollinen toteutus Go:ssa:

Miten se toimii? Kierrämme jokaisen solmun ja laskemme sen hash-arvon. Hash-arvo palautetaan hash-funktiolla, joka tuottaa kokonaisluvun avaimen (syötteemme) ja solmun tunnisteen perusteella (helpoin tapa on hashata näiden kahden merkkijonon ketjutus). Sitten palautamme solmun, jonka hash-arvo on suurin. Tästä syystä algoritmi tunnetaan myös nimellä korkeimman satunnaispainon hashaus.

Rendezvous-algoritmin suurin haittapuoli on sen O(n)-aikakompleksisuus, jossa n on solmujen lukumäärä. Se on erittäin tehokas, jos tarvitsemme rajallisen määrän solmuja. Kuitenkin jos alamme ylläpitää tuhansia solmuja, se saattaa alkaa aiheuttaa suorituskykyongelmia.

Ring Consistent Hash

Seuraava algoritmi julkaistiin vuonna 1997 Karger et al. artikkelissa. Tässä tutkimuksessa mainittiin ensimmäistä kertaa termi consistent hashing.

Se perustuu renkaaseen (päästä päähän yhdistetty joukko). Vaikka se on suosituin consistent hashing -algoritmi (tai ainakin tunnetuin), periaatetta ei aina ymmärretä hyvin. Sukelletaanpa siihen.

Aluksi luodaan rengas. Rengas on kiinteän pituinen. Esimerkissämme jaamme sen 12 osaan:

Sitten sijoitamme solmut. Esimerkissämme määrittelemme N0, N1 ja N2.

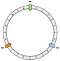
Solmut jaetaan toistaiseksi tasaisesti. Palaamme tähän kohtaan myöhemmin.

Sitten on aika katsoa, miten avaimet esitetään. Ensin tarvitsemme funktion f, joka palauttaa rengasindeksin (0-11) avaimen perusteella. Voimme käyttää siihen mod-n-hashingia. Koska renkaan pituus on vakio, se ei aiheuta meille ongelmia.

Esimerkissämme määrittelemme 3 avainta: a, b ja c. Sovellamme f jokaiseen niistä. Oletetaan, että saamme seuraavat tulokset:

• f(a) = 1
• f(a) = 5
• f(a) = 7

Voidaan siis sijoittaa näppäimet rinkiin näin:

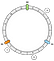
Miten liitämme tietyn avaimen solmuun? Tärkein logiikka on eteneminen. Annetusta avaimesta palautamme ensimmäisen solmun, jonka löydämme seuraavaksi edetessämme eteenpäin:

Tässä esimerkissä assosioimme solmun a solmuun N1, solmuun b ja solmuun c solmuun N2.

Katsotaanpa seuraavaksi, miten tasapainottaminen onnistuu. Määrittelemme toisen solmun N3. Mihin meidän pitäisi sijoittaa se? Enää ei ole tilaa sille, että kokonaisjakauma olisi tasainen. Pitäisikö meidän järjestää solmut uudelleen? Ei, muuten emme olisi enää yhdenmukaisia, eikö niin? Solmun sijoittamiseksi käytämme uudelleen samaa hash-funktiota f, jonka otimme käyttöön. Sen sijaan, että sitä kutsuttaisiin avaimella, sitä voidaan kutsua solmun tunnisteella. Uuden solmun sijainti päätetään siis satunnaisesti.

Tällöin herää yksi kysymys: mitä teemme a:lle, kun seuraava solmu ei ole enää N1:

Ratkaisu on seuraava: Meidän on muutettava sen assosiaatio ja saatava a assosioitumaan N3:

Kuten aiemmin totesimme, ideaalisen algoritmin pitäisi tasapainottaa keskimäärin 1/n prosenttia avaimista uudelleen. Esimerkissämme, kun lisäämme neljännen solmun, 25 prosenttia mahdollisista avaimista pitäisi yhdistää uudelleen N3:aan. Onko näin?

• N0 indekseistä 8-12: 33,3 % kaikista avaimista
• N1 indekseistä 2-4: 16,6 % kaikista avaimista
• N2 indekseistä 4-8: 33.3 % kaikista avaimista
• N3 indekseistä 0-2: 16,6 % kaikista avaimista

Jakauma ei ole tasainen. Miten voimme parantaa sitä? Ratkaisu on käyttää virtuaalisia solmuja.

Sitotaan, että sen sijaan, että sijoitamme yhden pisteen per solmu, voimme sijoittaa kolme. Lisäksi meidän on määriteltävä kolme erilaista hashing-funktiota. Jokainen solmu hashataan kolme kertaa, joten saamme kolme erilaista indeksiä:

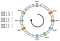
Voidaan soveltaa samaa algoritmia siirtymällä eteenpäin. Silti avain liitettäisiin solmuun riippumatta siitä, minkä virtuaalisolmun se tapasi.

Juuri tässä esimerkissä jakauma olisi nyt seuraava:

• N0: 33,3 %
• N1: 25 %
• N2: 41,6 %

Mitä useamman virtuaalisolmun määrittelemme solmua kohden, sitä tasaisemmaksi jakauman pitäisi tulla. Kun palvelinta kohti on keskimäärin 100 virtuaalisolmua, vakiojakauma on noin 10 %. Kun käytössä on 1000, se on noin 3,2 %.

Tämä mekanismi on hyödyllinen myös, jos meillä on erikokoisia solmuja. Jos esimerkiksi yksi solmu on konfiguroitu käsittelemään teoriassa kaksi kertaa enemmän kuormaa kuin muut, voimme pyörittää kaksi kertaa enemmän virtuaalisia solmuja.

Virtuaalisten solmujen suurin haittapuoli on kuitenkin muistijalanjälki. Jos joudumme käsittelemään tuhansia palvelimia, se vaatisi megatavuja muistia.

Ennen kuin siirrymme eteenpäin, on mielenkiintoista huomata, että joskus algoritmia voidaan parantaa huomattavasti muuttamalla pientä osaa. Näin on esimerkiksi Googlen vuonna 2017 julkaisemassa algoritmissa nimeltä consistent hashing with bounded loads. Tämä versio perustuu samaan rengasideaan, jonka kuvasimme. Heidän lähestymistapansa on kuitenkin suorittaa pieni tasapainotus jokaisen päivityksen (uuden avaimen tai solmun lisääminen/poistaminen) yhteydessä. Tämä versio päihittää alkuperäisen version standardipoikkeaman suhteen huonoimman aikakompleksisuuden vastapainoksi.

Jump Consistent Hash

Vuonna 2007 kaksi Googlen insinööriä julkaisi jump consistent hashin. Verrattuna rengaspohjaiseen algoritmiin tämä toteutus ”ei vaadi tallennustilaa, on nopeampi ja tekee parempaa työtä avainavaruuden jakamisessa tasaisesti kauhojen kesken ja työmäärän jakamisessa tasaisesti kauhojen määrän muuttuessa”. Toisin sanottuna se parantaa työmäärän jakautumista solmujen kesken (ämpäri on sama käsite kuin solmu) ilman muistin ylikuormitusta.

Tässä on algoritmi C++-kielellä (7 riviä koodia 🤯):

Rengaskonsistentissa hashissa 1000 virtuaalisella solmulla standardipoikkeama oli noin 3,2 %. Hyppykonsistentissa hashissa emme enää tarvitse virtuaalisolmujen käsitettä. Silti standardipoikkeama on edelleen alle 0,0000001 %.

Tässä on kuitenkin yksi rajoitus. Solmut on numeroitava juoksevasti. Jos meillä on luettelo palvelimista foo, bar ja baz, emme voi poistaa esimerkiksi bar. Jos kuitenkin konfiguroimme tietovaraston, voimme soveltaa algoritmia saadaksemme shard-indeksin, joka perustuu shardien kokonaismäärään. Näin ollen hyppykonsistentti hash voi olla hyödyllinen shardauksen yhteydessä, mutta ei kuorman tasauksen yhteydessä.

Mikä on Perfect Consistent Hashing Algorithm?

Koska meillä on nyt jonkin verran kokemusta johdonmukaisesta hashauksesta, otetaan askel taaksepäin ja katsotaan, mikä olisi täydellinen algoritmi:

• Keskimäärin vain 1/n prosenttia avaimista siirrettäisiin uudelleen, missä n on solmujen lukumäärä.
• O(n) tilakompleksisuus, missä n on solmujen lukumäärä.
• O(1) aikakompleksisuus per solmun lisäys/poisto ja per avaimen haku.
• Minimaalinen standardipoikkeama, jolla varmistetaan, että solmu ei ole ylikuormitettu toiseen solmuun verrattuna.
• Se mahdollistaisi painon liittämisen solmuun selviytyäkseen solmujen erilaisesta mitoituksesta.
• Se mahdollistaisi solmujen mielivaltaisen nimen (ei juoksevaa numerointia) tukeakseen sekä kuorman tasausta että shardausta.

Valitettavasti tätä algoritmia ei ole olemassa. Nähdyn perusteella:

• Rendezvousilla on lineaarinen aikakompleksisuus per haku.
• Rengaskonsistentilla hashilla on huono minimaalinen keskihajonta ilman virtuaalisolmujen käsitettä. Virtuaalisolmujen kanssa on tilakompleksisuus O(n*v), jossa n on solmujen lukumäärä ja v virtuaalisolmujen lukumäärä solmua kohti.
• Hyppykonsistentilla hashilla ei ole vakioaikakompleksisuutta eikä se tue mielivaltaisia solmujen nimiä.

Aihe on edelleen avoinna, ja on olemassa viimeaikaisia tutkimuksia, joihin kannattaa tutustua. Esimerkiksi vuonna 2005 julkaistu multi-probe consistent hash. Se tukee O(1) avaruuskompleksisuutta. Silti ε:n standardipoikkeaman saavuttamiseksi se vaatii O(1/ε) aikaa per haku. Jos esimerkiksi halutaan saavuttaa alle 0,5 %:n standardipoikkeama, avain on hakattava noin 20 kertaa. Näin ollen voimme saavuttaa minimaalisen standardipoikkeaman, mutta suuremmalla haun aikakompleksisuuden vaivalla.

Kuten johdannossa totesimme, johdonmukaisista hashausalgoritmeista tuli valtavirtaa. Sitä käytetään nyt lukemattomissa järjestelmissä, kuten MongoDB:ssä, Cassandrassa, Riakissa, Akkassa jne. olipa kyse sitten kuorman tasaamisesta tai datan jakamisesta. Silti, kuten usein tietotekniikassa, jokaiseen ratkaisuun liittyy kompromisseja.

Kompromisseista puheen ollen, jos kaipaat jatkoa, kannattaa vilkaista Damian Gryskin kirjoittamaa erinomaista postausta: