Helppo johdatus koveran rungon ongelmaan

Konveksista rungoista on usein hyötyä monilla eri aloilla, joskus aivan odottamatta. Tässä artikkelissa selitän 2d-konveksisten runkojen perusidean ja kuinka käyttää graham-skannausta niiden löytämiseen. Jos siis tiedät jo graham-skannauksen, tämä artikkeli ei ole sinua varten, mutta jos et, tämän pitäisi tutustuttaa sinut joihinkin asiaankuuluviin käsitteisiin.

Pistejoukon kovera runko määritellään pienimmäksi koveraksi monikulmioksi, joka sulkee sisäänsä kaikki joukon pisteet. Konveksinen tarkoittaa, että monikulmion yksikään kulma ei ole sisäänpäin taipunut.

Punaiset reunat oikeanpuoleisessa monikulmiossa sulkevat sisäänsä kulman, jossa muoto on kovera, koveran vastakohta.

Hyödyllinen tapa ajatella koveraa runkoa on kuminauha-analogia. Kuvitellaan, että joukon pisteet olisivat nauloja, jotka työntyvät ulos tasaisesta pinnasta. Kuvittele nyt, mitä tapahtuisi, jos ottaisit kuminauhan ja venyttäisit sen naulojen ympärille. Kun kuminauha yrittäisi supistua takaisin alkuperäiseen pituuteensa, se ympäröisi naulat koskettamalla niitä, jotka työntyvät kauimmaksi keskipisteestä.

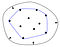
Tuloksena syntyvän kuperan rungon esittämiseksi koodissa tallennamme yleensä listan pisteistä, jotka pitävät tätä kuminauhaa pystyssä, eli listan pisteistä kuperalla rungolla.

Huomaa, että meidän on vielä määriteltävä, mitä pitäisi tapahtua, jos kolme pistettä on samalla viivalla. Jos kuvitellaan, että kuminauhalla on piste, jossa se koskettaa yhtä naulaa, mutta se ei taivu siinä kohtaa lainkaan, se tarkoittaa, että naula sijaitsee siinä kohdassa kahden muun naulan välisellä suoralla. Ongelmasta riippuen voimme pitää tätä suoralla linjalla olevaa naulaa osana tuotosta, koska se koskettaa kuminauhaa. Toisaalta voimme myös sanoa, että tämän naulan ei pitäisi olla osa tulosta, koska kuminauhan muoto ei muutu, kun poistamme sen. Tämä päätös riippuu ongelmasta, jota olet parhaillaan työstämässä, ja mikä parasta, jos sinulla on tulo, jossa yksikään kolmesta pisteestä ei ole kollineaarinen (näin on usein ohjelmointikilpailujen helpoissa tehtävissä), voit jopa jättää tämän ongelman kokonaan huomioimatta.

Konveksin rungon löytäminen

Katsomalla pistejoukkoa inhimillinen intuitio antaa meille mahdollisuuden selvittää nopeasti, mitkä pisteet koskettavat todennäköisesti konveksia rungon kohtia ja mitkä pisteet ovat lähemmäs keskipistettä, ja ovat siten kaukana konveksista rungosta. Mutta tämän intuition kääntäminen koodiksi vaatii hieman työtä.

Pistejoukon kuperan rungon löytämiseksi voimme käyttää algoritmia nimeltä Graham-skannaus, jota pidetään yhtenä ensimmäisistä laskennallisen geometrian algoritmeista. Tämän algoritmin avulla voimme löytää osajoukon pisteitä, jotka sijaitsevat koveralla rungolla, sekä järjestyksen, jossa nämä pisteet kohtaavat kierrettäessä koveraa runkoa.

Algoritmi alkaa etsimällä pisteen, jonka tiedämme varmasti sijaitsevan koveralla rungolla. Esimerkiksi pistettä, jolla on pienin y-koordinaatti, voidaan pitää varmana valintana. Jos samalla y-koordinaatilla on useita pisteitä, otetaan se, jolla on suurin x-koordinaatti (tämä toimii myös muiden kulmapisteiden kanssa, esim. ensin pienin x, sitten pienin y).

Seuraavaksi lajittelemme muut pisteet sen kulman mukaan, jossa ne sijaitsevat aloituspisteestä katsottuna. Jos kaksi pistettä sattuu olemaan samassa kulmassa, lähtöpistettä lähempänä olevan pisteen pitäisi esiintyä lajittelussa aikaisemmin.

Algoritmin ideana on nyt kävellä tämän lajitellun matriisin ympärillä määrittämällä jokaisen pisteen kohdalla, sijaitseeko se kuperalla kuorella vai ei. Tämä tarkoittaa, että jokaisen kohtaamamme pistekolmikon kohdalla päätämme, muodostavatko ne kuperan vai koveran kulman. Jos kulma on kovera, tiedämme, että tämän kolmion keskimmäinen piste ei voi sijaita koveralla rungolla.

(Huomaa, että termejä kovera ja kovera kulma on käytettävä suhteessa koko monikulmioon, pelkkä kulma yksinään ei voi olla kovera tai kovera, koska siinä ei olisi mitään viittaussuuntaa.)

Tallennamme koveralla rungolla olevat pisteet pinoon, jolloin voimme lisätä pisteitä, jos saavutamme ne matkalla lajiteltujen pisteiden ympäri, ja poistaa ne, jos huomaamme niiden muodostavan koveran kulman.

(Tarkkaan ottaen meidän on päästävä käsiksi pinon kahteen ylimpään pisteeseen, joten käytämme sen sijaan std::vector, mutta ajattelemme sitä eräänlaisena pinona, koska olemme aina huolissamme vain parista ylimmästä elementistä.)

Kierrämme lajiteltua pistejoukkoa, lisäämme pisteen pinoon, ja jos myöhemmin huomaamme, että piste ei kuulu koveraan runkoon, poistamme sen.

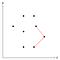
Voidaan mitata, taipuuko kulloinenkin kulma sisäänpäin vai ulospäin laskemalla ristitulo ja tarkistamalla, onko se positiivinen vai negatiivinen. Yllä olevassa kuvassa on kolmikko pisteitä, joiden muodostama kulma on kupera, joten näistä kolmesta pisteestä keskimmäinen jää toistaiseksi pinoon.

Jatketaan seuraavaan pisteeseen ja jatketaan samaa: tarkistetaan, onko kulma kupera, ja jos ei, poistetaan piste. Sitten jatketaan lisäämällä seuraava piste ja toistetaan.

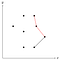
Punaisella merkitty kulma on kovera, joten poistamme pinoista keskimmäisen pisteen, koska se ei voi olla osa kuperaa runkoa.

Miten tiedämme, että näin saamme oikean vastauksen?

Tarkan todistuksen kirjoittaminen ei kuulu tämän artikkelin piiriin, mutta voin kirjoittaa perusajatukset ylös. Rohkaisen sinua kuitenkin jatkamaan ja yrittämään täyttää aukot!

Koska laskimme ristitulon jokaisessa kulmassa, tiedämme varmasti, että saamme kuperan monikulmion. Nyt meidän täytyy vain todistaa, että tämä kovera monikulmio todella sulkee sisäänsä kaikki pisteet.

(Itse asiassa sinun täytyy myös osoittaa, että tämä on pienin mahdollinen kovera monikulmio, joka täyttää nämä ehdot, mutta se seuraa melko helposti siitä, että koveran monikulmion kulmapisteet ovat alkuperäisen pistejoukon osajoukko.)

Esitetään, että on olemassa piste P juuri löytämämme monikulmion ulkopuolella.

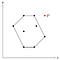
Koska kaikki pisteet on lisätty pinoomme kertaalleen, tiedämme, että piste P on jossain vaiheessa poistettu pinoomme. Tämä tarkoittaa, että P muodosti yhdessä naapuripisteidensä, sanotaan niitä O:ksi ja Q:ksi, kanssa koveran kulman.

Koska O ja Q sijaitsevat monikulmion sisäpuolella (tai sen rajalla), myös P:n täytyisi sijaita rajan sisäpuolella, koska monikulmio on kupera ja kulma, jonka O ja Q muodostavat P:n kanssa, on monikulmion suhteen kovera.

Olemme siis havainneet ristiriitaisuuden, joka tarkoittaa sitä, että sellaista pistettä P:n kanssa ei voi olla.

Toteutus

Tässä annetussa toteutuksessa on funktio convex_hull, joka ottaa std::vector, joka sisältää pisteet std::pairs inteinä ja palauttaa toisen std::vector, joka sisältää ne pisteet, jotka sijaitsevat koveralla rungolla.

Ajan ja muistin analyysi

On aina hyödyllistä ajatella monimutkaisuusalgoritmeja Big-O-merkintätavalla, jota en selitä tässä, koska Michael Olorunnisola täällä on jo tehnyt paljon parempaa työtä sen selittämisessä kuin minä luultavasti tekisin:

Pisteiden lajitteluun kuluu aluksi O(n log n)-aikaa, mutta sen jälkeen jokainen askel voidaan laskea vakioajassa. Jokainen piste lisätään pinoon ja poistetaan pinosta korkeintaan kerran, mikä tarkoittaa, että pahimmassa tapauksessa ajoaika on O(n log n).

Muistinkäyttöä, joka tällä hetkellä on O(n), voitaisiin optimoida poistamalla pinon tarve ja suorittamalla operaatiot suoraan syötemassalla. Voisimme siirtää kuperan rungon päällä olevat pisteet syötemäärän alkuun ja järjestää ne oikeaan järjestykseen, ja muut pisteet siirrettäisiin loppumäärään. Funktio voisi tällöin palauttaa vain yhden kokonaislukumuuttujan, joka ilmaisee kuperan rungon päällä olevien pisteiden määrän. Tällä on tietysti se haittapuoli, että funktio muuttuu paljon monimutkaisemmaksi, joten en suosittele sitä, ellet koodaa sulautettuja järjestelmiä varten tai ellei sinulla ole vastaavalla tavalla rajoittavia muistihuolia. Useimmissa tilanteissa virhetodennäköisyyden/muistin säästön kompromissi ei vain ole sen arvoinen.

Muut algoritmit

Vaihtoehto Grahamin skannaukselle on Chanin algoritmi, joka perustuu käytännössä samaan ideaan mutta on helpompi toteuttaa. On kuitenkin järkevää ensin ymmärtää, miten Graham Scan toimii.

Jos tunnet itsesi todella hienostuneeksi ja haluat ratkaista ongelman kolmessa ulottuvuudessa, tutustu Preparatan ja Hongin algoritmiin, jonka he esittelivät vuonna 1977 julkaistussa artikkelissaan ”Convex Hulls of Finite Sets of Points in Two and Three Dimensions”.