Helmholtz-resonanssi
- Helmholtz-resonanssin analysointi
- Resonanssi, impedanssi, vaihe- ja taajuusriippuvuus
- Komplikaatioita, joihin liittyy pituus
- Helmholtz-resonanssit ja kitarat
Helmholtz-resonanssin analysointi
Nyt mennään kvantitatiivisuuteen: Oletetaan ensinnäkin, että tuotetun äänen aallonpituus on paljon pidempi kuin resonaattorin mitat. Tämän sivun yläosassa olevan animaation pullojen aallonpituudet ovat 180 ja 74 cm, joten tämä approksimaatio on melko hyvä, mutta se kannattaa tarkistaa aina, kun aletaan kuvata jotain Helmholtz-oskillaattoriksi. Tämän approksimaation seurauksena voimme jättää huomiotta paineen vaihtelut säiliön tilavuuden sisällä: paineen värähtelyllä on sama vaihe kaikkialla säiliön sisällä.
Olkoon kaulassa olevalla ilmalla tehollinen pituus L ja poikkipinta-ala S. Sen massa on tällöin SL kertaa ilman tiheys ρ. (Joitakin teholliseen pituuteen liittyviä komplikaatioita käsitellään tämän sivun lopussa). Jos tämä ilman ”tulppa” laskeutuu pienen matkan x pulloon, se puristaa säiliössä olevan ilman niin, että aiemmin tilavuuden V täyttäneen ilman tilavuus on nyt V – Sx. Näin ollen tuon ilman paine nousee ilmakehän paineesta PA korkeampaan arvoon PA + p.
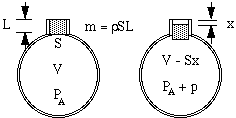
Nyt voisi ajatella, että paineen nousu olisi vain verrannollinen tilavuuden pienenemiseen. Näin olisi, jos kokoonpuristuminen tapahtuisi niin hitaasti, että lämpötila ei muuttuisi. Äänen synnyttävissä värähtelyissä muutokset ovat kuitenkin nopeita, joten lämpötila nousee puristuksessa, jolloin paineen muutos on suurempi. Teknisesti ottaen ne ovat adiabaattisia eli lämpö ei ehdi liikkua, ja tuloksena olevaan yhtälöön sisältyy vakio γ, ominaislämpöjen suhde, joka on noin 1,4 ilmalle. (Tämä selitetään liitteessä.) Näin ollen pienen tilavuudenmuutoksen ΔV aiheuttama paineenmuutos p on vain
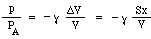
Nyt massaa m liikuttaa kaulan ylä- ja alapuolen välinen paine-ero eli nettovoima pS, joten kirjoitamme kiihtyvyydelle a Newtonin lain:
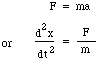
Korvaamalla F ja m saadaan: 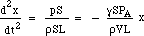
Palauttava voima on siis verrannollinen siirtymään. Tämä on yksinkertaisen harmonisen liikkeen ehto, ja sen taajuus on 1/2π kertaa verrannollisuusvakion neliöjuuri, joten
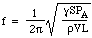
Nyt äänen nopeus c ilmassa määräytyy tiheyden, paineen ja ominaislämpöjen suhteen mukaan, joten voimme kirjoittaa:
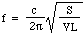
Laitetaanpa muutamia lukuja: 1 litran pullolle, jonka S = 3 neliösenttimetriä ja L = 5 senttimetriä, taajuus on 130 Hz, joka on noin C:n alapuolella keskimmäisen C:n kohdalla. (Ks. muistiinpanot.) Aallonpituus on siis 2,6 metriä, joka on paljon suurempi kuin pullo. Tämä oikeuttaa jälkikäteen johdannon alussa tehdyn oletuksen.
Resonanssi, impedanssi, vaihe- ja taajuusriippuvuus
Tämän kappaleen voi lukea itsekseen, mutta jos haluat yksityiskohtaisempaa taustaa, katso Oskillaatioita, Pakotettuja oskillaatioita ja Akustinen yhteensopivuus, inertanssi ja impedanssi.
Palaamme mekaaniseen esitykseen ja tarkastelemme Helmholtz-resonaattoria ulkopuolelta, kuten ensimmäisessä kaaviossa on esitetty: Työnnämme värähtelevällä voimalla F, taajuudella f ,massaa m (ilmaa resonaattorin kaulassa), joka on tuettu jousella (suljettu ilma), jonka jousivakio on k ja jonka toinen pää on kiinteä (resonaattorissa oleva ilma ei pääse karkaamaan). Epärealistisesti jätämme (toistaiseksi) huomiotta painovoiman ja kitkan.
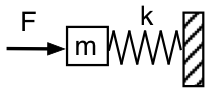
Massan kiihdyttämiseen tarvittava voima on verrannollinen kiihtyvyyteen ja siten verrannollinen f2:een. Riittävän matalalla taajuudella massan kiihdyttämiseen tarvittava voima on mitättömän pieni, joten F:n on vain puristettava ja venytettävä jousi. Tässä raja-arvossa sovellettu voima F = +kx. (Jousivoima on -kx.) Järjestelmän mekaaninen impedanssi on tällä matalalla taajuudella taipuvainen tai jousimainen. Akustisesti se näyttää akustiselta mukautuvuudelta: työnnämme ilmamassaa kaulassa ja puristamme ilmaa resonaattorissa. Oikealle kohdistettu voima F on vaiheittain oikealle mitatun x:n kanssa, joten se on 90° nopeuden takana ja kohdistettu paine on 90° akustisen virtauksen takana resonaattorissa.
Muista, että f2 riippuvuus kiihtyvyydestä. Riittävän suurella taajuudella jousivoima on siis mitätön verrattuna massaa kiihdyttävään voimaan. F on siis vaiheessa kiihtyvyyden kanssa, jolloin se on 90° edellä nopeutta. Akustisesti sovellettu paine on 90° ennen resonaattoriin tulevaa akustista virtausta. Se on mekaaninen tai akustinen inertanssi.
Resonanssitaajuudella (puhutaan edelleen yllä olevasta luonnoksesta) amplitudi voi olla suuri hyvin pienellä voimalla. Resonanssissa impedanssi on siis hyvin pieni, kun tarkastellaan massaan ulkopuolelta kohdistuvaa voimaa (kaavio yllä). Resonanssissa virtaus resonaattoriin ja resonaattorista ulos on suurin.
Katsotaan nyt, mitä tapahtuu, jos tarkastellaan painetta resonaattorin sisällä (kaulasta poispäin). Tässä tarkastelemme jouseen kohdistuvaa voimaa, joten mekaaninen analogiamme näyttää tältä kaaviokuvalta.
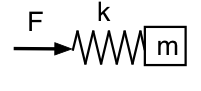
Tällä kertaa matala taajuus tarkoittaa, että voima voi olla pieni tietyllä amplitudilla: jousi ja massa liikkuvat yhdessä massana, ja systeemi näyttää tällä kertaa inertiltä matalalla taajuudella. Suurella taajuudella massa ei juurikaan liiku, ja systeemi on jousimaisen tai taipuisa. Vaihesuhteet ovat siis päinvastaiset kuin aiemmin: pienellä f:llä p johtaa U:ta 90°; suurella f:llä p jää jälkeen U:sta 90°.
Komplikaatiot, joihin liittyy tehollinen pituus
Tämän sivun ensimmäisessä kaaviossa ilman ”tulppa” on piirretty ikään kuin se olisi sylinteri, joka päättyy siististi pullon kaulan molempiin päihin. Tämä on liian yksinkertaista. Käytännössä pullon kaulassa olevan ilman mukana liikkuu ylimääräinen tilavuus sekä sisä- että ulkopuolella – kuten yllä olevassa animaatiossa esitetään. Kaulan geometriseen pituuteen lisättävä lisäpituus on tyypillisesti (ja hyvin likimääräisesti) 0,6 kertaa säde ulkopäässä ja yksi säde sisäpäässä).
|
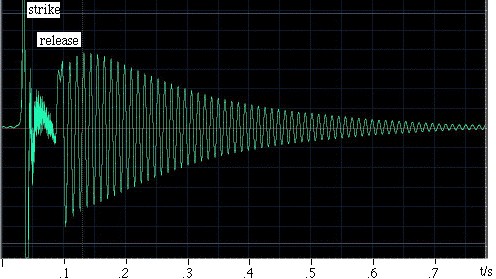
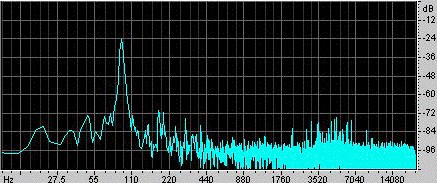
Esim. Ra Inta teki tämän esimerkin. Hän otti pallomaisen Helmholtz-resonaattorin, jonka tilavuus on 0,00292 m3 ja jonka sylinterinmuotoinen kaula on 0,080 m pitkä ja poikkipinta-ala 0,00083 m2. Herättääkseen sen hän löi sitä kämmenellä ja vapautti sen sitten. Resonaattorin sisällä oleva mikrofoni tallentaa äänen, joka näkyy vasemmalla olevassa oskillogrammissa. Näet, että käsi sulkee resonaattorin melko alle 0,1 sekunnin ajaksi ja että tänä aikana värähtelyt ovat heikompia ja suhteellisen korkeataajuisia. Heti kun käsi päästetään irti, syntyy värähtely, joka vähitellen häviää, kun se menettää energiaa viskoosisen ja turbulenttisen vastuksen sekä äänisäteilyn kautta. Lähempi tarkastelu osoittaa, että taajuus nousee hieman käden siirtyessä poispäin avoimesta päästä, koska käsi rajoittaa säteilyyn käytettävissä olevaa avaruuskulmaa ja lisää siten päätyvaikutusta (tai päätykorjausta). Kaulan pituutta kasvattaa yksi verhoiltu ja yksi verhoilematon päätevaikutus, jolloin kaulan teholliseksi pituudeksi saadaan 0,105 m. Äänen nopeuden ollessa 343 m/s yllä oleva lauseke antaa resonanssitaajuudeksi 90 Hz. |
|
Helmholtz-resonanssit ja kitarat
* Sanoin edellä, että kitaran rungossa oleva ilma toimii lähes kuin Helmholtz-oskillaattori. Tämä tapaus on monimutkainen, koska runko voi hieman paisua, kun ilmanpaine sen sisällä nousee – ja myös siksi, että kitaran ääniaukossa ”olevalla” ilmalla on geometria, jota on vaikeampi havainnollistaa kuin pullon kaulassa olevaa ilmaa. Kitaran rungon tapauksessa ilman tulpan pituus on nimittäin suunnilleen yhtä pitkä kuin vain muutaman millimetrin paksuisen ”putken” päässä olevat kaksi ”päätehostetta”. Päätysefektit ovat kuitenkin suhteessa ja samankokoisia kuin reiän säde, joten ilman massa on huomattava. Lieriönmuotoisen putken, joka avautuu äärettömään, tasaiseen ohjauslevyyn, päätyvaikutuksen pituus on 0,85 kertaa putken säde. Vaikka kitaran äänilauta ei ole ääretön, olisi odotettavissa samanlainen päätevaikutus, joten ilman ”tulpan” tehollinen pituus olisi noin 1,7 kertaa reiän säde. (Jotkut valmistajat lisäävät tätä määrää kiinnittämällä ääniaukon alapuolelle lyhyen putken, jonka säde on sama.)
Pari ihmistä on kirjoittanut ja kysynyt, kuinka suuri ääniaukon pitäisi olla tietyssä soittimessa. No, voimme käyttää yllä olevaa yhtälöä aluksi vastaamaan tähän kysymykseen. Rungon turpoaminen on kuitenkin tärkeää. Se tekee ilman ”jousituksesta” melko pehmeämpää, ja siten laskee taajuutta. Puhtaasti Helmholtz-resonanssia voidaan tutkia pitämällä rungon tilavuus vakiona. Tätä mitattaessa yleinen käytäntö on haudata kitara hiekkaan, jotta estetään rungon turpoaminen tai ”hengittäminen”. Kitaroita ei kuitenkaan yleensä soiteta tässä tilanteessa. Helmholtzin laskelma antaa siis yliarvion todellisen, joustavan rungon resonanssitaajuudesta.
Oletetaan pyöreä ääniaukko, jonka säde on r, joten S = πr2 ja L = 1,7r kuten edellä on selitetty. Kun korvaamme Helmholtzin taajuuden yhtälöön käyttäen c = 340 m/s, saamme:
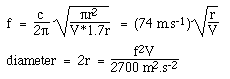
Huomaa, että käytämme SI-standardiyksiköitä: olemme käyttäneet äänen nopeutta metreinä ja sekunteina, joten tilavuuden on oltava kuutiometreinä ja taajuuden hertseinä, jotta vastaus olisi metreinä.
Asia on monimutkaisempi, kun ääniaukot eivät ole pyöreitä, koska loppuvaikutus ei ole sama kuin saman pinta-alan omaavalla ympyrällä. Tohtoriopiskelija ja luuttumestari John McLennan on kirjoittamassa raporttia muutamista mittauksista tästä, jonka julkaisemme pian täällä.
Kitara- ja viuluperheen soittimissa Helmholtzin (plus rungon) resonanssi on usein lähellä toiseksi matalimman jousen taajuutta tai hieman sen alapuolella, viulussa D:n tienoilla tai kitarassa G-A:n tienoilla. Voit pienentää tai siirtää Helmholtzin taajuutta huomattavasti peittämällä reiän kokonaan tai osittain sopivasti muotoillulla jäykällä pahvipalalla. Jos sitten soitat nuotin lähellä resonanssia ja liu’utat pahvia niin, että se vuoroin peittää ja vuoroin paljastaa reiän, kuulet selvästi resonanssin vaikutuksen.
Onko 0.85r vaikutus järkevä? Ra Inta, joka teki väitöskirjan kitaran akustiikasta laboratoriossamme, ehdottaa mielenkiintoista demonstraatiota:
Kostuta kitaran jouset niin, etteivät ne värähtele (esim. nenäliina jousien ja sormilautojen väliin). Pidä toisen käden kämmentä ääniaukon yläpuolella ja lähellä sitä. Iske toisen kätesi sormella äänilautaan terävä isku lähelle ääniaukkoa ja lähelle 1. säiettä. Tunnet ilmapulssin kämmenelläsi. Sormen isku työntää äänilautaa sisään ja puristaa hieman ilmaa ulos rungosta. Siirrä nyt kätesi vähitellen kauemmas soittoreiästä ja jatka naputtelua sormella. Milloin lakkaat tuntemasta ilman liikettä? Näin saat karkean arvion ”loppuvaikutuksen” pituudesta ääniaukon tapauksessa.
Helmholtzin resonanssin virittäminen
Tämän laboratorion tohtorikoulutettavan John McLennanin julkaisujen joukossa on artikkeli, jossa hän varioi Helmholtzin resonanssia äänen nopeutta muuttamalla.
- McLennan, J.E. (2003) ”A0- ja A1-tutkimukset viulussa käyttäen CO2:ta, He:tä ja ilman ja heliumin seoksia”. Acustica, 89, 176-180.
Joitakin kuvia historiallisista Helmholtz-resonaattoreista on toimittanut Thomas B. Greenslade, Kenyon College, Ohio.
Leave a Reply