Greenin funktio

Generally speaking, Greenin funktio on integraaliydin, jota voidaan käyttää ratkaisemaan differentiaaliyhtälöitä lukuisista perheistä, mukaan lukien yksinkertaisemmat esimerkit, kuten tavalliset differentiaaliyhtälöt alku- tai reunaehtojen kanssa, sekä vaikeammat esimerkit, kuten inhomogeeniset osittaisdifferentiaaliyhtälöt (PDE) reunaehtojen kanssa. Useista syistä tärkeät Greenin funktiot mahdollistavat voimanlähteeseen tai pisteeseen keskittyneeseen varaukseen liittyvien toimien visuaalisen tulkinnan (Qin 2014), mikä tekee niistä erityisen hyödyllisiä sovelletun matematiikan aloilla. Erityisesti Greenin funktioiden menetelmiä käytetään laajasti mm, fysiikassa ja tekniikassa.

Tarkemmin sanottuna, kun annetaan lineaarinen differentiaalioperaattori , joka vaikuttaa jakaumien kokoelmaan jonkin euklidisen avaruuden osajoukon yli, Greenin funktio pisteessä , joka vastaa , on

(1)

jossa tarkoittaa delta-funktiota. Motivaatio tällaisen funktion määrittelyyn on laaja, mutta kertomalla yllä oleva identiteetti funktiolla ja integroimalla suhteessa saadaan

(2)

Oikea puoli redusoituu pelkäksi deltafunktion ominaisuuksien vuoksi, ja koska on lineaarinen operaattori, joka vaikuttaa vain :iin eikä :iin, voidaan vasen puoli kirjoittaa uudelleen muotoon

(3)

Tämä reduktio on erityisen hyödyllinen, kun ratkaistaan differentiaaliyhtälöitä, jotka ovat muotoa

(4)

jossa ylläoleva aritmetiikka vahvistaa, että

(5)

ja josta seuraa, että on erityinen integraalimuoto

(6)

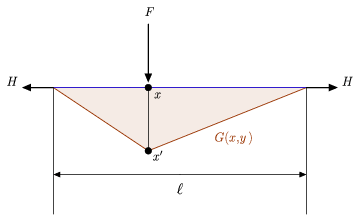
Yllä oleva kuva havainnollistaa sekä intuitiivista fysikaalista tulkintaa Greenin funktiosta että suhteellisen yksinkertaista siihen liittyvää differentiaaliyhtälöä, johon yllä olevaa määritelmää voidaan verrata (Hartmann 2013). Siinä esitetään erityisesti kahden seinän väliin ripustettu kireä köysi, jonka pituus on ja jota pitää paikallaan sen kumpaankin päähän kohdistuva identtinen vaakavoima sekä köyden johonkin sisäpisteeseen kohdistuva sivuttaiskuorma . Olkoon piste, joka vastaa taipunutta köyttä, olettakaamme, että alaspäin suuntautuva voima on vakio, sanotaan , ja merkitään köyden taipumaa. Tätä fysikaalista systeemiä vastaa differentiaaliyhtälö

(7)

for , jossa , systeemi, jonka yksinkertaisuuden ansiosta sekä sen ratkaisu että sen Greenin funktio voidaan kirjoittaa eksplisiittisesti:

(8)

ja

(9)

jotka vastaavat. Kuten yllä olevasta kuvasta käy ilmi, siirtyneellä köydellä on edellä annettu kappaleittain lineaarinen muoto, mikä vahvistaa väitteen, että tähän systeemiin liittyvä Greenin funktio edustaa vaakasuoran köyden toimintaa, joka vastaa voiman kohdistamista.

Greenin funktiota, joka ottaa argumenttiparin , kutsutaan toisinaan kaksipisteiseksi Greenin funktioksi. Tämä on vastakohta monipisteisille Greenin funktioille, jotka ovat erityisen tärkeitä monikappaleteorian alalla.

Elementaarisena esimerkkinä edellä määritellystä kahden pisteen funktiosta tarkastellaan ongelmaa, jossa määritetään potentiaali , jonka synnyttää varausjakauma, jonka varaustiheys on , jolloin Poissonin yhtälön ja Coulombin lain soveltaminen kunkin varauksen elementin tuottamaan potentiaaliin antaa ratkaisun

(10)

mikä pätee, tietyin edellytyksin alueella, jossa . Koska oikeaa puolta voidaan tarkastella integraalioperaattorina, joka muuntaa muotoon , voidaan tämä ratkaisu kirjoittaa uudelleen Greenin funktion , jolla on muoto

(11)

jolloin ratkaisu voidaan kirjoittaa uudelleen:

(12)

(Arfken 2012).

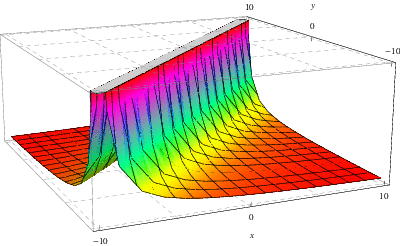
Yllä olevassa kuvassa on esitetty edellä käsitellyn –-yhtälön – ratkaisuun liittyvä Greenin funktio, jossa täällä, ja , vastaavasti , on piirretty -, vastaavasti -, akselille.

Jossain määrin kattavaa luetteloa eri differentiaaliyhtälöitä vastaavista Greenin funktioista ylläpitää verkossa Kevin Cole (Cole 2000).

Johtuen Greenin funktioista kirjoitetun kirjallisuuden moninaisuudesta, voi syntyä useita erilaisia merkintätapoja ja määritelmiä, joista osa poikkeaa temaattisesti edellä esitetystä, mutta jotka eivät yleensä vaikuta tulosten tärkeisiin ominaisuuksiin. Kuten yllä oleva esimerkki osoittaa, esimerkiksi jotkut kirjoittajat haluavat merkitä muuttujia ja mieluummin vektoreiden ja avulla korostaakseen sitä, että ne ovat :n elementtejä jollakin :llä, joka voi olla suurempi kuin 1 (Arfken 1985). Suhteellisen yleistä on myös nähdä määritelmä negatiivisella merkillä siten, että määritellään funktioksi, jolle

(13)

mutta koska tämä puhtaasti fysikaalinen tarkastelu ei vaikuta taustalla olevaan matematiikkaan, tämä näkökulma jätetään yleensä huomiotta. Greenin funktiolle tunnetaan myös useita muita merkintätapoja, joista eräitä ovat pienen käyttö sijasta (Stakgold 1979) sekä pystyviivan lisääminen pilkun sijasta, esim, (Duffy 2001).

Toisissa tapauksissa kirjallisuudessa esitetään määritelmiä, jotka liittyvät läheisesti niihin yhteyksiin, joissa ne esitetään. Esimerkiksi jotkut kirjoittajat määrittelevät Greenin funktiot funktioiksi, jotka täyttävät tietyn joukon ehtoja, esim. olemassaolo tietynlaisella alueella, liittyminen hyvin erityiseen differentiaalioperaattoriin tai täsmällisten reunaehtojen täyttyminen. Yksi yleisimmistä tällaisista esimerkeistä löytyy muistiinpanoista, joita on laatinut mm, Speckiltä, jossa Greenin funktio määritellään täyttämään pisteille ja kaikille pisteille , jotka sijaitsevat Omega:n :n Omega:n :n rajoilla (Speck 2011). Tämä erityinen määritelmä esittää integraaliytimen, joka vastaa yleistetyn Poissonin yhtälön ratkaisua, ja sen vuoksi siihen kohdistuisi ilmeisiä rajoituksia, kun sitä mukautetaan yleisempään asetelmaan. Toisaalta tällaiset esimerkit eivät ole vailla etujaan. Esimerkiksi yllä olevan yleistetyn Poissonin esimerkin tapauksessa jokainen tällainen Greenin funktio voidaan jakaa siten, että

(14)

jossa ja säännölliselle Laplacianille (Hartman 2013). Tällaisissa tilanteissa tunnetaan taustalla olevan differentiaaliyhtälön perusratkaisuna ja sen säännöllisenä ratkaisuna; näin ollen ja kutsutaan toisinaan :n perus- ja säännölliseksi osaksi.

Yleisen Greenin funktion useat perusominaisuudet seuraavat välittömästi (tai melkein) sen määritelmästä ja siirtyvät kaikkiin erityistapauksiin. Jos esimerkiksi operaattorin ydin ei ole triviaali, yhteen operaattoriin voi liittyä useita Greenin funktioita, minkä vuoksi on oltava varovainen, kun puhutaan ”siitä” Greenin funktiosta. Greenin funktiot täyttävät adjunktiosymmetrian kahdessa argumentissaan siten, että

(15)

jossa tässä määritellään yhtälön

Tässä on :n adjunktio. Yksi välitön seuraus tästä tosiasiasta on, että itseadjungoituneille operaattoreille on symmetrinen:

(17)

Tätä identiteettiä kutsutaan usein vastavuoroisuusperiaatteeksi, ja se sanoo fysikaalisesti ilmaistuna, että yksikkölähteen aiheuttama vaste kohdassa on sama kuin yksikkölähteen aiheuttama vaste yksikkövoiman kohdassa aiheuttama vaste kohdassa (Stakgold 1979).

Minkä tahansa Greenin funktion olennainen ominaisuus on, että se tarjoaa tavan kuvata mielivaltaisen differentiaaliyhtälön ratkaisun vastetta jonkinlaiselle lähdetermille jonkin määrän reunaehtojen vallitessa (Arfken et al. 2012). Joidenkin kirjoittajien mielestä Greenin funktiolla on osittaisdifferentiaaliyhtälöiden teoriassa suunnilleen samanlainen rooli kuin Fourierin sarjoilla tavallisten differentiaaliyhtälöiden ratkaisussa (Mikula ja Kos 2006).

Abstraktimpia skenaarioita varten on olemassa useita käsitteitä, jotka toimivat kontekstikohtaisina analogeina Greenin funktion käsitteelle. Esimerkiksi funktionaalianalyysissä on usein hyödyllistä tarkastella niin sanottua yleistettyä Greenin funktiota, jolla on monia analogisia ominaisuuksia, kun se integroidaan abstraktisti funktioiden sijasta funktioita vastaan. Tällaiset yleistykset ovatkin synnyttäneet täysin analogisen teoreettisen PDE-analyysin haaran, ja ne ovat itsessään suuren tutkimusmäärän kohteena.