Gram-Schmidt-prosessi
by Marco Taboga, PhD
Gram-Schmidt-prosessi (tai -proseduuri) on operaatioiden sarja, jonka avulla lineaarisesti riippumattomien vektoreiden joukko voidaan muuttaa ortonormaalisten vektoreiden joukoksi, joka kattaa saman avaruuden, jonka alkuperäinen joukko kattaa.

Alkusanat
Käydään läpi joitakin käsitteitä, jotka ovat olennaisia Gram-Schmidt-prosessin ymmärtämiseksi.
Muistetaan, että kahden vektorin  ja
ja  sanotaan olevan ortogonaalisia, jos ja vain jos niiden sisäinen tuote on yhtä suuri kuin nolla, eli
sanotaan olevan ortogonaalisia, jos ja vain jos niiden sisäinen tuote on yhtä suuri kuin nolla, eli 
Sisäisen tuotteen ollessa kyseessä voimme määritellä vektorin  normin (pituuden) seuraavasti:
normin (pituuden) seuraavasti:
Vektorijoukkoa kutsutaan ortonormaaliksi, jos ja vain jos sen alkioilla on yksikkönormi ja ne ovat kohtisuorassa toisiinsa nähden. Toisin sanoen  vektorijoukko
vektorijoukko  on ortonormaali, jos ja vain jos
on ortonormaali, jos ja vain jos
Olemme todistaneet, että ortonormaalin joukon vektorit ovat lineaarisesti riippumattomia.
Kun vektoriavaruuden perusta on myös ortonormaali joukko, sitä sanotaan ortonormaaliksi perustaksi.
Projektiot ortonormaaleille joukoille
Gram-Schmidt-prosessissa käytämme toistuvasti seuraavaa lausetta, joka osoittaa, että jokainen vektori voidaan hajottaa kahteen osaan: 1) sen projektioon ortonormaalille joukolle ja 2) residuaaliin, joka on ortogonaalinen annetulle ortonormaalille joukolle.
Lauseke Olkoon  vektoriavaruus, joka on varustettu sisäisellä tuotteella
vektoriavaruus, joka on varustettu sisäisellä tuotteella  . Olkoon
. Olkoon  ortonormaali joukko. Kaikille
ortonormaali joukko. Kaikille  on
on  missä
missä  on ortogonaalinen
on ortogonaalinen  kaikille
kaikille 
määritelmä Tällöin jokaiselle
Tällöin jokaiselle  on, että
on, että missä: vaiheissa
missä: vaiheissa  ja
ja  olemme käyttäneet hyväksi sitä tosiasiaa, että sisäinen tuote on lineaarinen ensimmäisessä argumentissaan; askeleessa
olemme käyttäneet hyväksi sitä tosiasiaa, että sisäinen tuote on lineaarinen ensimmäisessä argumentissaan; askeleessa  olemme käyttäneet sitä tosiasiaa, että
olemme käyttäneet sitä tosiasiaa, että  jos
jos  , koska kyseessä on ortonormaali joukko; askeleessa
, koska kyseessä on ortonormaali joukko; askeleessa  olemme käyttäneet sitä tosiasiaa, että
olemme käyttäneet sitä tosiasiaa, että  :n normi on 1. Näin ollen
:n normi on 1. Näin ollen  , kuten edellä on määritelty, on ortogonaalinen kaikille ortonormaalijoukon alkioille, mikä todistaa lauseen.
, kuten edellä on määritelty, on ortogonaalinen kaikille ortonormaalijoukon alkioille, mikä todistaa lauseen.
Termiä  kutsutaan
kutsutaan  :n lineaariprojektioksi ortonormaalijoukkoon
:n lineaariprojektioksi ortonormaalijoukkoon  , kun taas termiä
, kun taas termiä  kutsutaan lineaariprojektion residuaaliksi.
kutsutaan lineaariprojektion residuaaliksi.
Normalisointi
Toinen ehkä itsestään selvä tosiasia, jota tulemme toistuvasti käyttämään Gram-Schmidt-prosessissa, on se, että jos otamme minkä tahansa nollasta poikkeavan vektorin ja jaamme sen sen normilla, niin jaon tuloksena saadaan uusi vektori, jolla on yksikkönormi.
Toisin sanoen, jos  , niin normin määrällisyysominaisuuden nojalla meillä on, että
, niin normin määrällisyysominaisuuden nojalla meillä on, että 
Tämän seurauksena voimme määritellä ja normin positiivisuuden ja absoluuttisen homogeenisuuden nojalla, meillä on
ja normin positiivisuuden ja absoluuttisen homogeenisuuden nojalla, meillä on
Yleiskatsaus menettelyyn
Nyt kun tiedämme, miten vektori normalisoidaan ja miten se hajotetaan projektioksi ortonormaalijoukkoon ja jäännökseksi, olemme valmiita selittämään Gram-Schmidt-menettelyn.
Annamme yleiskatsauksen prosessista, jonka jälkeen ilmaisemme sen muodollisesti lauseena ja käsittelemme kaikki tekniset yksityiskohdat lauseen todistuksessa.
Tässä on yleiskatsaus.
Annetaan joukko lineaarisesti riippumattomia vektoreita  .
.
Aluksi normalisoimme ensimmäisen vektorin, eli määrittelemme
Toisessa vaiheessa projisoimme 
 :
: :
: jossa
jossa  on projisoinnin jäännös.
on projisoinnin jäännös.
Sitten normalisoimme residuaalin:
Myöhemmin todistamme, että  (jotta normalisointi voidaan suorittaa) koska lähtövektorit ovat lineaarisesti riippumattomia.
(jotta normalisointi voidaan suorittaa) koska lähtövektorit ovat lineaarisesti riippumattomia.
Näin saadut kaksi vektoria  ja
ja  ovat ortonormaaleja.
ovat ortonormaaleja.
Kolmannessa vaiheessa projisoimme  vektoreihin
vektoreihin  ja
ja  :
: ja laskemme projisoinnin residuaalin
ja laskemme projisoinnin residuaalin  .
.
Sitten normalisoimme sen:
Jatkamme näin, kunnes saamme viimeisen normalisoidun residuaalin  .
.
Prosessin lopussa vektorit  muodostavat ortonormaalin joukon, koska:
muodostavat ortonormaalin joukon, koska:
-
ne ovat normalisoinnin tulosta, ja näin ollen niillä on yksikkönormi;
-
jokainen
 saadaan residuaalista, jolla on se ominaisuus, että se on ortogonaalinen
saadaan residuaalista, jolla on se ominaisuus, että se on ortogonaalinen  :lle.
:lle.
Tämän yleiskatsauksen täydentämiseksi muistutetaan, että  :n lineaariväli on kaikkien niiden vektoreiden joukko, jotka voidaan kirjoittaa
:n lineaariväli on kaikkien niiden vektoreiden joukko, jotka voidaan kirjoittaa  :n lineaarikombinaatioina; sitä merkitään
:n lineaarikombinaatioina; sitä merkitään  ja se on lineaarinen avaruus.
ja se on lineaarinen avaruus.
Koska vektorit  ovat
ovat  :n lineaarisesti riippumattomia kombinaatioita, mikä tahansa vektori, joka voidaan kirjoittaa
:n lineaarisesti riippumattomia kombinaatioita, mikä tahansa vektori, joka voidaan kirjoittaa  :n lineaarikombinaatioksi, voidaan kirjoittaa myös
:n lineaarikombinaatioksi, voidaan kirjoittaa myös  :n lineaarikombinaatioksi. Näin ollen näiden kahden vektorijoukon välit ovat yhtenevät:
:n lineaarikombinaatioksi. Näin ollen näiden kahden vektorijoukon välit ovat yhtenevät:
Formaali lausuma
Formalisoimme tässä Gram-Schmidt-prosessin lauseeksi, jonka todistus sisältää kaikki menettelyn tekniset yksityiskohdat.
Asema Olkoon  vektoriavaruus, joka on varustettu sisäisellä tuotteella
vektoriavaruus, joka on varustettu sisäisellä tuotteella  . Olkoon
. Olkoon  lineaarisesti riippumattomia vektoreita. Silloin on olemassa joukko ortonormaaleja vektoreita
lineaarisesti riippumattomia vektoreita. Silloin on olemassa joukko ortonormaaleja vektoreita  siten, että
siten, että jokaiselle
jokaiselle  .
.
Todistus tapahtuu induktiolla: ensin todistetaan, että lause on tosi  :lle, ja sitten todistetaan, että se on tosi geneeriselle
:lle, ja sitten todistetaan, että se on tosi geneeriselle  :lle, jos se pätee
:lle, jos se pätee  :lle. Kun
:lle. Kun  , vektorilla
, vektorilla on yksikkönormi ja se muodostaa itsessään ortonormaalin joukon: muita vektoreita ei ole, joten ortogonaalisuusehto täyttyy triviaalisti. Joukko
on yksikkönormi ja se muodostaa itsessään ortonormaalin joukon: muita vektoreita ei ole, joten ortogonaalisuusehto täyttyy triviaalisti. Joukko on kaikkien niiden
on kaikkien niiden  :n skalaarikertojen joukko, jotka ovat myös
:n skalaarikertojen joukko, jotka ovat myös  :n skalaarikertoja (ja päinvastoin). Näin ollen,
:n skalaarikertoja (ja päinvastoin). Näin ollen,  Ja nyt oletetaan, että lause on tosi
Ja nyt oletetaan, että lause on tosi  :lle. Silloin voimme projisoida
:lle. Silloin voimme projisoida  kohtaan
kohtaan  :
: , jossa jäännös
, jossa jäännös  on ortogonaalinen
on ortogonaalinen  :lle. Oletetaan, että
:lle. Oletetaan, että  . Silloin,
. Silloin, Jos oletuksen mukaan
Jos oletuksen mukaan  mille tahansa
mille tahansa  , on
, on  mille tahansa
mille tahansa  , missä
, missä  ovat skalaareja. Näin ollen,
ovat skalaareja. Näin ollen, Muilla sanoilla, oletus, että
Muilla sanoilla, oletus, että  johtaa johtopäätökseen, että
johtaa johtopäätökseen, että  on lineaarikombinaatio
on lineaarikombinaatio  . Mutta tämä on mahdotonta, koska yksi lauseen oletuksista on, että
. Mutta tämä on mahdotonta, koska yksi lauseen oletuksista on, että  ovat lineaarisesti riippumattomia. Tästä seuraa, että on oltava, että
ovat lineaarisesti riippumattomia. Tästä seuraa, että on oltava, että  . Voimme siis normalisoida residuaalin ja määritellä vektorin
. Voimme siis normalisoida residuaalin ja määritellä vektorin , jolla on yksikkönormi. Tiedämme jo, että
, jolla on yksikkönormi. Tiedämme jo, että  on ortogonaalinen
on ortogonaalinen  :lle. Tästä seuraa, että myös
:lle. Tästä seuraa, että myös  on ortogonaalinen
on ortogonaalinen  :lle. Näin ollen
:lle. Näin ollen  on ortonormaali joukko. Otetaan nyt mikä tahansa vektori
on ortonormaali joukko. Otetaan nyt mikä tahansa vektori  , joka voidaan kirjoittaa muodossa
, joka voidaan kirjoittaa muodossa , jossa
, jossa  ovat skalaareja. Koska oletuksen
ovat skalaareja. Koska oletuksen  mukaan yhtälö (2) voidaan kirjoittaa myös muodossa
mukaan yhtälö (2) voidaan kirjoittaa myös muodossa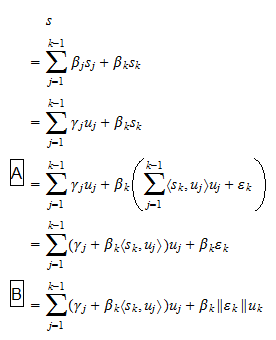 jossa
jossa  ovat skalaareja, ja: askeleessa
ovat skalaareja, ja: askeleessa  olemme käyttäneet yhtälöä (1); askeleessa
olemme käyttäneet yhtälöä (1); askeleessa  olemme käyttäneet määritelmää
olemme käyttäneet määritelmää  . Näin olemme todistaneet, että jokainen vektori, joka voidaan kirjoittaa
. Näin olemme todistaneet, että jokainen vektori, joka voidaan kirjoittaa  :n lineaarikombinaatioksi, voidaan kirjoittaa myös
:n lineaarikombinaatioksi, voidaan kirjoittaa myös  :n lineaarikombinaatioksi. Oletus (3) mahdollistaa käänteisen todistamisen täysin analogisella tavalla:
:n lineaarikombinaatioksi. Oletus (3) mahdollistaa käänteisen todistamisen täysin analogisella tavalla: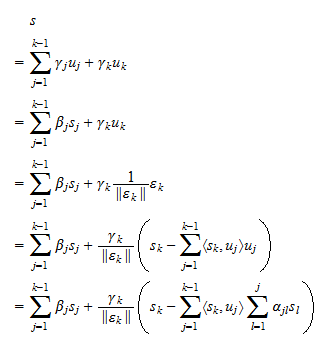 Toisin sanoen jokainen
Toisin sanoen jokainen  :n lineaarikombinaatio on myös
:n lineaarikombinaatio on myös  :n lineaarikombinaatio. Tämä todistaa, että
:n lineaarikombinaatio. Tämä todistaa, että  ja päättää todistuksen.
ja päättää todistuksen.
Jokaisella sisäisen tuotteen avaruudella on ortonormaali perusta
Seuraava propositio esittää tärkeän seurauksen Gram-Schmidt-prosessista.
Propositio Olkoon  vektoriavaruus, joka on varustettu sisäisellä tuotteella
vektoriavaruus, joka on varustettu sisäisellä tuotteella  . Jos
. Jos  :llä on äärellinen ulottuvuus
:llä on äärellinen ulottuvuus  , niin
, niin  :lle on olemassa ortonormaali perusta
:lle on olemassa ortonormaali perusta  .
.
Sen vuoksi, että  on äärellisulotteinen,
on äärellisulotteinen,  :lle
:lle  on olemassa vähintään yksi perusta, joka koostuu
on olemassa vähintään yksi perusta, joka koostuu  vektoreista
vektoreista  . Voimme soveltaa Gram-Schmidt-menettelyä perustaan ja saada ortonormaalijoukon
. Voimme soveltaa Gram-Schmidt-menettelyä perustaan ja saada ortonormaalijoukon  . Koska
. Koska  on perusta, se kattaa
on perusta, se kattaa  . Näin ollen
. Näin ollen 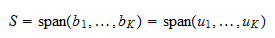 Siten
Siten  on
on  :n ortonormaali perusta.
:n ortonormaali perusta.
Ratkaistuja harjoituksia
Alla on muutamia harjoituksia selitettyine ratkaisuineen.
Harjoitus 1
Tarkastellaan avaruutta  kaikista
kaikista  vektoreista, joilla on reaaliset merkinnät ja sisäinen tuote
vektoreista, joilla on reaaliset merkinnät ja sisäinen tuote , jossa
, jossa  ja
ja  on
on  transponointi. Määritellään vektori
transponointi. Määritellään vektori
Normalisoidaan  .
.
Normin  normi on
normi on Siten,
Siten,  :n normi on
:n normi on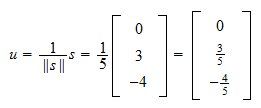
Harjoitus 2
Tarkastellaan avaruutta  kaikista
kaikista  vektoreista, joilla on reaaliset merkinnät ja sisäinen tuote
vektoreista, joilla on reaaliset merkinnät ja sisäinen tuote , jossa
, jossa  . Tarkastellaan kahta lineaarisesti riippumatonta vektoria
. Tarkastellaan kahta lineaarisesti riippumatonta vektoria
Muunnetaan ne ortonormaalijoukoksi Gram-Schmidtin prosessin avulla.
Normin  normi on
normi on  Siten, ensimmäinen ortonormaali vektori on
Siten, ensimmäinen ortonormaali vektori on
 :n ja
:n ja  :n sisäinen tulo on
:n sisäinen tulo on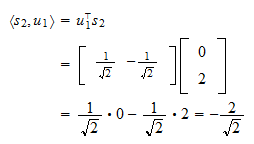
 :n projektio
:n projektio  :lle on
:lle on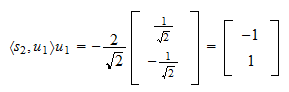 Projektion jäännös on
Projektion jäännös on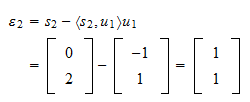 Jäännöksen normisto on
Jäännöksen normisto on ja normalisoitu jäännös on
ja normalisoitu jäännös on Tässä, etsimämme ortonormaali joukko on
Tässä, etsimämme ortonormaali joukko on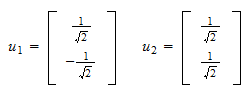
How to cite
Please cite as:
Taboga, Marco (2017). ”Gram-Schmidtin prosessi”, Luentoja matriisialgebrasta. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.
Leave a Reply