Gibbs Sampling

Kuten myös muut MCMC-menetelmät, Gibbs-näytteenottaja rakentaa Markovin ketjun, jonka arvot konvergoituvat kohti tavoitejakaumaa. Gibbs-näytteenotto on itse asiassa Metropolis-Hastings-algoritmin erityistapaus, jossa ehdotukset hyväksytään aina.

Tarkemmin sanottuna oletetaan, että halutaan ottaa näytteitä monimuuttujaisesta todennäköisyysjakaumasta.

Huomautus: Monimuuttujainen todennäköisyysjakauma on usean muuttujan funktio (esim. 2-ulotteinen normaalijakauma).

Emmekä tiedä, miten jälkimmäisestä voidaan ottaa otos suoraan. Jonkin matemaattisen mukavuuden tai ehkä pelkän tuurin vuoksi satumme kuitenkin tietämään ehdolliset todennäköisyydet.

Tässä kohtaa Gibbs-näytteenotto tulee kuvaan. Gibbs-näytteenotto soveltuu silloin, kun yhteisjakaumaa ei tunneta eksplisiittisesti tai siitä on vaikea ottaa näytteitä suoraan, mutta kunkin muuttujan ehdollinen jakauma tunnetaan ja siitä on helpompi ottaa näytteitä.

Aloitetaan valitsemalla satunnaismuuttujille X & Y alkuarvo. Sitten otetaan näytteet X:n ehdollisesta todennäköisyysjakaumasta, kun Y = Y⁰ on annettu Y = Y⁰, jota merkitään nimellä p(X|Y|Y⁰). Seuraavassa vaiheessa otamme otoksen uudesta Y:n arvosta, joka on riippuvainen juuri laskemastamme X¹:stä. Toistamme menettelyä vielä n – 1 iteraation ajan vuorotellen ottamalla uuden otoksen X:n ehdollisesta todennäköisyysjakaumasta ja Y:n ehdollisesta todennäköisyysjakaumasta toisen satunnaismuuttujan senhetkisen arvon perusteella.

Katsotaanpa esimerkkiä. Oletetaan, että meillä on seuraavat posterioriset ja ehdolliset todennäköisyysjakaumat.

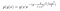
jossa g(y) sisältää ne termit, jotka eivät sisällä x:ää, ja g(x) sisältää ne, jotka eivät riipu y:stä.

Me emme tiedä C:n (normalisointivakio) arvoa. Tiedämme kuitenkin ehdolliset todennäköisyysjakaumat. Siksi voimme käyttää Gibbs Samplingia posteriorijakauman approksimointiin.

Huomautus: Ehdolliset todennäköisyydet ovat itse asiassa normaalijakaumia, ja ne voidaan kirjoittaa uudelleen seuraavasti.

Kun otetaan huomioon edellä esitetyt yhtälöt, siirrymme toteuttamaan Gibbs Sampling-algoritmia Python-ohjelmalla. Aluksi tuomme seuraavat kirjastot.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

Määritellään posteriorijakauman funktio (oletetaan C=1).

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

Sitten piirretään todennäköisyysjakauma.

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Yritämme nyt estimoida todennäköisyysjakaumaa Gibbs Samplingin avulla. Kuten aiemmin mainitsimme, ehdolliset todennäköisyydet ovat normaalijakaumia. Siksi voimme ilmaista ne mu:n ja sigman avulla.

Seuraavassa koodilohkossa määrittelemme funktiot mu:lle ja sigmalle, alustamme satunnaismuuttujamme X & Y ja asetamme N:n (iteraatioiden määrä).

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

Käymme läpi Gibbs-näytteenotto-algoritmin.

for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x

Lopuksi piirrämme tulokset.

plt.hist(x, bins=50);
plt.hist(y, bins=50);

Gibbs Sampling -algoritmilla saatu todennäköisyysjakauma lähentää hyvin tavoitejakaumaa.

Johtopäätös

Gibbsin näytteenotto on Monte Carlo Markovin ketjumenetelmä, joka piirtää iteratiivisesti instanssin kunkin muuttujan jakaumasta ehdollisena muiden muuttujien nykyisistä arvoista monimutkaisten yhteisten jakaumien estimoimiseksi. Toisin kuin Metropolis-Hastings-algoritmissa, ehdotus hyväksytään aina. Siten Gibbs Sampling voi olla paljon tehokkaampi.