Differentiaaliyhtälöt – Eigenvalues and Eigenfunctions
Näytä Mobiili-ilmoitus Näytä kaikki muistiinpanot Piilota kaikki muistiinpanot
Luku 8-2 : Ominaisarvot ja ominaistoiminnot
Kuten teimme edellisessä luvussa, meidän on jälleen kerran todettava, että aiomme antaa vain lyhyen katsauksen aiheeseen ominaistoiminnot ja ominaistoiminnot itseisarvo-ongelmissa. On olemassa melko paljon ideoita, joita emme tarkastele tässä. Tämän jakson tarkoituksena on vain antaa sinulle käsitys aiheesta ja tehdä tarpeeksi työtä, jotta voimme ratkaista joitakin perusparittaisdifferentiaaliyhtälöitä seuraavassa luvussa.
Nyt ennen kuin alamme puhua tämän jakson varsinaisesta aiheesta, muistutetaanpa erästä lineaarialgebran aihetta, jota käsittelimme lyhyesti aiemmin näissä muistiinpanoissa. Jos tietylle neliömatriisille \(A\) löytyisi \(\lambda \) arvoja, joille löytyisi nollasta poikkeavia ratkaisuja eli \(\vec x \ne \vec 0\),
\
tällöin kutsuisimme \(\lambda \) \(A\):n omaksi arvoksi ja \(\vec x\):n vastaavaksi omaksi vektoriksi.
On tärkeää muistaa tässä yhteydessä, että jotta \(\lambda \) olisi itseisarvo, meidän täytyi pystyä löytämään yhtälölle nollasta poikkeavia ratkaisuja.
Mitä tekemistä tällä on raja-arvo-ongelmien kanssa? No palatkaa edelliseen kappaleeseen ja katsokaa esimerkkiä 7 ja esimerkkiä 8. Näissä kahdessa esimerkissä ratkaisimme homogeenisia (ja se on tärkeää!) BVP:itä muodossa,
\
Esimerkissä 7 meillä oli \(\lambda = 4\) ja löysimme ei-triviaaleja (eli nollasta poikkeavia) ratkaisuja BVP:lle. Esimerkissä 8 käytimme \(\lambda = 3\) ja ainoa ratkaisu oli triviaali ratkaisu (eli \(y\left( t \right) = 0\)). Tämä homogeeninen BVP (muistetaan, että tämä tarkoittaa myös sitä, että reunaehdot ovat nolla) näyttää siis käyttäytyvän samalla tavalla kuin edellä esitetty matriisiyhtälö. On olemassa \(\lambda \) arvoja, jotka antavat ei-triviaaleja ratkaisuja tähän BVP:hen, ja \(\lambda \) arvoja, jotka sallivat vain triviaalin ratkaisun.
Siten niiden \(\lambda \) arvojen osalta, jotka antavat ei-triviaaleja ratkaisuja, kutsumme \(\lambda \):tä BVP:n ominaisarvoksi ja ei-triviaaleja ratkaisuja kutsutaan BVP:n ominaisfunktioiksi, jotka vastaavat kyseistä ominaisarvoa.
Tiedämme nyt, että kohdassa \(\eqref{eq:eq1}\) annetulle homogeeniselle BVP:lle \(\lambda = 4\) on ominaissuure (jonka ominaissuureet \(y\left( x \right) = {c_2}\sin \left( {2x} \right)\)) ja että \(\lambda = 3\) ei ole ominaissuure.
Tulevaisuudessa yritämme selvittää, onko \(\eqref{eq:eq1}\):lle olemassa muita ominaisarvoja, mutta ennen sitä kommentoidaan lyhyesti, miksi tässä keskustelussa on niin tärkeää, että BVP on homogeeninen. Edellisen jakson esimerkeissä 2 ja 3 ratkaisimme homogeenisen differentiaaliyhtälön
\
kahdella eri epähomogeenisella reunaehdolla muodossa,
\
Näissä kahdessa esimerkissä näimme, että yksinkertaisesti muuttamalla \(a\) ja/tai \(b\) arvoa pystyimme saamaan joko epätriviaaleja ratkaisuja tai pakottamaan ratkaisun puuttumisen kokonaan. Kun keskustelemme ominaisarvoista/eigenfunktioista, tarvitsemme ratkaisuja, jotka ovat olemassa, ja ainoa tapa varmistaa tämä käyttäytyminen on vaatia, että myös reunaehdot ovat homogeeniset. Toisin sanoen, tarvitsemme BVP:n olevan homogeeninen.
On yksi viimeinen aihe, josta meidän on keskusteltava, ennen kuin siirrymme omien arvojen ja ominaistoimintojen aiheeseen, ja tämä on enemmänkin merkityskysymys, joka auttaa meitä joissakin tehtävissä, joita meidän on tehtävä.
Asettakaamme, että meillä on toisen kertaluvun differentiaaliyhtälö ja että sen ominaispolynomilla on kaksi reaalista, erillistä juurta ja että ne ovat muotoa
\
Tällöin tiedämme, että ratkaisu on,
\
Vaikka tässä ratkaisussa ei ole mitään vikaa, kirjoitetaan tämä hieman uudelleen. Aloitamme jakamalla termit seuraavasti,
\
Nyt lisäämme/substrahoimme seuraavat termit (huomaa, että ”sekoitamme” \({c_i}\) ja \( \pm \,\alpha \) uusiin termeihin) saadaksemme,
\
Seuraavaksi järjestellään termejä hieman uudelleen,
\
Viimeiseksi suluissa olevat määrät kertovat ja siirretään myös murtoluvun sijaintia. Tekemällä tämän sekä nimeämällä uudet vakiot uudelleen saamme,
\
Kaikki tämä työ tuntuu luultavasti hyvin salaperäiseltä ja tarpeettomalta. Siihen oli kuitenkin todella syy. Itse asiassa olet ehkä jo nähnyt syyn, ainakin osittain. Kaksi ”uutta” funktiota, jotka meillä on ratkaisussamme, ovat itse asiassa kaksi hyperbolista funktiota. Erityisesti,
\
Siten toinen tapa kirjoittaa ratkaisu toisen kertaluvun differentiaaliyhtälölle, jonka ominaispolynomilla on kaksi reaalista, erillistä juurta muodossa \({r_1} = \alpha ,\,\,\,{r_2} = – \,\alpha \), on,
\
Jos meillä on ratkaisu tässä muodossa joillekin (itse asiassa useimmille) tarkastelemillemme pulmille, se tekee elämästämme paljon helpompaa. Hyperbolisilla funktioilla on joitakin erittäin mukavia ominaisuuksia, joita voimme (ja tulemme) hyödyntämään.
Ensiksi, koska tarvitsemme niitä myöhemmin, derivaatat ovat,
\
Seuraavaksi tarkastellaan nopeasti näiden funktioiden kuvaajia.
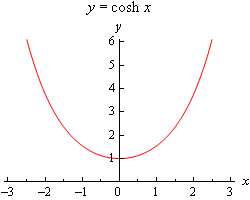

Huomaa, että \(\cosh \left( 0 \right) = 1\) ja \(\sinh \left( 0 \right) = 0\). Koska työskentelemme usein reunaehtojen kanssa kohdassa \(x = 0\), nämä ovat käyttökelpoisia arvioita.
Seuraavaksi, ja ehkä vielä tärkeämpää, huomataan, että \(\cosh \left( x \right) > 0\) kaikille \(x\), joten hyperbolinen kosini ei koskaan ole nolla. Samoin voimme nähdä, että \(\sinh \left( x \right) = 0\) vain jos \(x = 0\). Tulemme käyttämään näitä molempia tosiasioita joissakin töissämme, joten meidän ei kannata unohtaa niitä.
Okei, nyt kun olemme saaneet kaiken tämän pois tieltä, tehdäänpä esimerkki, jossa nähdään, miten etsitään BVP:n ominaissuureita/ominaistoimintoja.
Aloitimme tämän jakson tarkastelemalla tätä BVP:tä ja tiedämme jo yhden ominaisarvon (\(\lambda = 4\)) ja tiedämme yhden arvon \(\lambda \), joka ei ole ominaisarvo (\(\lambda = 3\)). Kun käymme läpi tätä työtä, meidän on muistettava, että saamme ominaisarvon tietylle \(\lambda \) arvolle, jos saamme ei-triviaaleja BVP-ratkaisuja kyseiselle \(\lambda \) arvolle.
Tietääksemme, että olemme löytäneet kaikki ominaissuureet, emme voi vain ruveta kokeilemaan satunnaisesti ominaissuureiden arvoja nähdäksemme saammeko ei-triviaaleja ratkaisuja vai emme. Onneksi on olemassa tapa tehdä tämä, joka ei ole liian huono ja antaa meille kaikki ominaisarvot/eigenfunktiot. Meidän on kuitenkin tehtävä joitakin tapauksia. Kolme tapausta, joita meidän on tarkasteltava, ovat : \(\lambda > 0\), \(\lambda = 0\) ja \(\lambda < 0\). Jokainen näistä tapauksista antaa BVP:n ratkaisulle tietyn muodon, johon voimme sitten soveltaa reunaehtoja nähdaksemme, saammeko ei-triviaaleja ratkaisuja vai emme. Aloitetaan siis tapausten käsittely.
\(\underline {\lambda > 0} \)
Tässä tapauksessa ominaispolynomi, jonka saamme differentiaaliyhtälöstä, on,
\
Tässä tapauksessa, koska tiedämme, että \(\lambda > 0\) nämä juuret ovat kompleksisia ja voimme kirjoittaa ne sen sijaan,
\
Differentiaaliyhtälön yleinen ratkaisu on tällöin,
\
Soveltamalla ensimmäistä reunaehtoa saamme,
\
Tämä huomioon ottaen ja soveltamalla toista reunaehtoa saamme,
\
Tämä tarkoittaa, että meillä on oltava jompikumpi seuraavista,
\
Muistutetaan kuitenkin, että haluamme ei-triviaaleja ratkaisuja, ja jos meillä on ensimmäinen mahdollisuus, saamme triviaalin ratkaisun kaikille \:n arvoille(\lambda > 0\). Oletetaan siis, että \({c_2} \ne 0\). Tämä tarkoittaa, että meillä on,
\
Toisin sanoen, hyödyntämällä sitä, että tiedämme, missä sini on nolla, voimme päästä toiseen yhtälöön. Huomaa myös, että koska oletamme, että \(\lambda > 0\) tiedämme, että \(2\pi \sqrt \lambda > 0\)ja näin ollen \(n\) voi olla vain positiivinen kokonaisluku tässä tapauksessa.
Nyt meidän tarvitsee vain ratkaista tämä \(\lambda \) ja saamme kaikki positiiviset ominaissuureet tälle BVP:lle.
Positiiviset itseisarvot ovat siis,
\
ja näitä itseisarvoja vastaavat ominaistoiminnot ovat,
\
Huomaa, että merkitsimme \(n\) alaviivalla \(n\) ominaistoimintoihin ja ominaistoimintoihin merkitäksemme sitä, että jokaiselle annetulle \(n\)-arvolle on yksi. Huomaa myös, että jätimme \({c_2}\) pois ominaistoimintojen kohdalta. Ominaisfunktioiden kohdalla olemme kiinnostuneita vain itse funktiosta emmekä sen edessä olevasta vakiosta, joten jätämme sen yleensä pois.
Siirrymme nyt toiseen tapaukseen.
\(\underline {\lambda = 0} \)
Tässä tapauksessa BVP:stä tulee,
\
ja integroimalla differentiaaliyhtälö pari kertaa saamme yleisen ratkaisun,
\
Soveltamalla ensimmäistä reunaehtoa saadaan,
\
Toisen reunaehdon sekä ensimmäisen reunaehdon tulosten soveltaminen antaa,
\
Tässä tapauksessa, toisin kuin ensimmäisessä tapauksessa, meillä ei ole valinnanvaraa, miten saamme tämän nollaksi. Tämä on nolla vain, jos \({c_2} = 0\).
Siten tämän BVP:n osalta (ja tämä on tärkeää), jos meillä on \(\lambda = 0\), ainoa ratkaisu on triviaaliratkaisu, joten \(\lambda = 0\) ei voi olla tämän BVP:n ominaisarvo.
Katsotaan nyt viimeistä tapausta.
\(\underline {\lambda < 0} \)
Tässä tapauksessa ominaisyhtälö ja sen juuret ovat samat kuin ensimmäisessä tapauksessa. Tiedämme siis, että,
\
Mutta koska oletamme tässä \(\lambda < 0\), nämä ovat nyt kaksi reaalista erillistä juurta, joten käyttämällä edellä tekemäämme työtä tällaisten reaalisten, erillisten juurien kohdalla tiedämme, että yleinen ratkaisu on,
\
Huomaa, että olisimme voineet käyttää eksponentiaalista ratkaisumuotoa tässä tapauksessa, mutta työmme helpottuu huomattavasti, jos käytämme tässä tapauksessa hyperbolista ratkaisumuotoa.
Nyt soveltamalla ensimmäistä reunaehtoa saadaan,
\
Soveltamalla toista reunaehtoa saadaan,
\
Koska oletamme \(\lambda < 0\), tiedämme, että \(2\pi \sqrt { – \lambda } \ne 0\) ja näin ollen tiedämme myös, että \(\sinh \left( {2\pi \sqrt { – \lambda } } \right) \ne 0\). Näin ollen, aivan kuten toisessa tapauksessa, meidän on oltava \({c_2} = 0\).
Tälle BVP:lle (tämäkin on tärkeää), jos meillä on \(\lambda < 0\), saamme vain triviaaliratkaisun, joten negatiivisia ominaisarvoja ei ole.
Yhteenvetona saamme siis tälle BVP:lle seuraavat ominaisarvot/eigenfunktiot.
\
Katsotaanpa vielä toinen esimerkki, jossa on hieman erilaiset reunaehdot.
Tässä työskentelemme derivaatan reunaehtojen kanssa. Työ on kuitenkin melko identtinen edellisen esimerkin kanssa, joten emme paneudu tässä aivan yhtä yksityiskohtaisesti. Meidän on käytävä läpi kaikki kolme tapausta aivan kuten edellisessä esimerkissä, joten aloitetaan siitä.
\(\underline {\lambda > 0} \)
Differentiaaliyhtälön yleinen ratkaisu on identtinen edellisen esimerkin kanssa, joten meillä on,
\
Soveltamalla ensimmäistä reunaehtoa saamme,
\
Muistutettakoon, että oletamme, että \(\lambda > 0\) on tässä tapauksessa \(\(\lambda > 0\), joten tämä on nolla vain, jos \(\({c_2} = 0\). Nyt toinen reunaehto antaa meille,
\
Muistetaan, että emme halua triviaaleja ratkaisuja ja että \(\lambda > 0\) joten saamme ei-triviaalin ratkaisun vain, jos edellytämme, että,
\
Ratkaisemalla \(\lambda \) näemme, että saamme täsmälleen samat positiiviset ominaissuureet tälle BVP:lle kuin edellisessä esimerkissä.
\
Näitä ominaisarvoja vastaavat ominaistoiminnot ovat kuitenkin,
\
Tälle BVP:lle saamme siis positiivisia ominaistoimintoja vastaavien ominaistoimintojen kosinukset.
Nyt toinen tapaus.
\(\underline {\lambda = 0} \)
Yleinen ratkaisu on,
\
Soveltamalla ensimmäistä reunaehtoa saadaan,
\
Käyttämällä tätä yleinen ratkaisu on tällöin,
\
ja huomaa, että tämä tyydyttää triviaalisti toisen reunaehdon,
\
Siten, toisin kuin ensimmäisessä esimerkissä, \(\lambda = 0\) on tämän BVP:n itseisarvo ja tätä itseisarvoa vastaava omaisuusfunktio on,
\
Huomaa jälleen, että jätimme pois mielivaltaisen vakion omaisuusfunktioita varten.
Hoidetaan lopuksi kolmas tapaus.
\(\underline {\lambda < 0} \)
Yleisratkaisu tässä on,
\
Soveltamalla ensimmäistä reunaehtoa saadaan,
\
Soveltamalla toista reunaehtoa saadaan,
\
Kuten edellisessä esimerkissä, tiedämme jälleen, että \(2\pi \sqrt { – \lambda } \ne 0\) ja siten \(\sinh \left( {2\pi \sqrt { – \lambda } } \right) \ne 0\). Näin ollen meillä on oltava \({c_1} = 0\).
Tälle BVP:lle ei siis taaskaan ole negatiivisia ominaisarvoja.
Yhteenvetona meillä on siis seuraavat ominaisarvot/ominaistoiminnot tälle BVP:lle.
\
Huomaa myös, että voimme itse asiassa yhdistellä näitä, jos sallimme \(n\)-luettelon ensimmäisen \(n\)-arvojen alkavan ykkösen nollasta. Tätä ei useinkaan tapahdu, mutta kun näin käy, hyödynnämme sitä. Tämän BVP:n ominaisarvojen/eigenfunktioiden ”virallinen” luettelo on siis,
\
Kahdessa edellisessä esimerkissä näimme, että meidän on yleisesti ottaen tarkasteltava \(\lambda \):n eri tapauksia, koska eri arvot johtavat usein erilaisiin yleisiin ratkaisuihin. Älä lukkiudu liikaa tapauksiin, jotka teimme tässä. Ratkaisemme useimmiten tämän tietyn differentiaaliyhtälön, joten on houkuttelevaa olettaa, että nämä ovat aina tapauksia, joita tarkastelemme, mutta on olemassa BVP:itä, jotka vaativat muita/eri tapauksia.
Also, kuten näimme kahdessa esimerkissä, joskus yksi tai useampi tapaus ei tuota yhtään ominaisarvoa. Näin tapahtuu usein, mutta meidän ei pitäisi lukea mitään siitä, että meillä ei ollut negatiivisia ominaisarvoja kummallekaan näistä kahdesta BVP:stä. On olemassa BVP:itä, joilla on negatiivisia ominaisarvoja.
Katsotaanpa toista esimerkkiä, jossa on hyvin erilaiset reunaehdot. Nämä eivät ole perinteisiä reunaehtoja, joita olemme tarkastelleet tähän asti, mutta näemme seuraavassa luvussa, miten niitä voi esiintyä tietyissä fysikaalisissa ongelmissa.
Tässä esimerkissä emme siis varsinaisesti määritä ratkaisua tai sen derivaattaa rajoilla. Sen sijaan määrittelemme yksinkertaisesti, että ratkaisun on oltava sama molemmilla rajoilla ja ratkaisun derivaatan on myös oltava sama molemmilla rajoilla. Lisäksi tämäntyyppinen reunaehto on tyypillisesti muotoa intervalli sen sijaan, mitä olemme työstäneet tähän asti.
Kuten edellä mainittiin, tämäntyyppisiä reunaehtoja esiintyy hyvin luontevasti tietyissä fysikaalisissa ongelmissa, ja näemme sen seuraavassa luvussa.
Kuten kahdessa edellisessä esimerkissä, meillä on vielä kolme vakiotapausta tarkasteltavana.
\(\underline {\lambda > 0} \)
Yleinen ratkaisu tälle tapaukselle on,
\
Soveltamalla ensimmäistä reunaehtoa ja käyttämällä hyväksi sitä tosiasiaa, että kosini on parillinen funktio (ts.\(\cos \left( { – x} \right) = \cos \left( x \right)\)) ja että sini on pariton funktio (eli \(\sin \left( { – x} \right) = – \sin \left( x \right)\)). antaa tulokseksi,
\
Tällä kertaa, toisin kuin kahdessa aiemmassa esimerkissä, tämä ei oikeastaan kerro meille mitään. Meillä voisi olla \(\sin \left( {\pi \sqrt \lambda } \right) = 0\), mutta on myös täysin mahdollista, ainakin tässä vaiheessa ongelmaa, että meillä olisi myös \({c_2} = 0\).
Mennään siis eteenpäin ja sovelletaan toista reunaehtoa ja katsotaan, saammeko siitä mitään irti.
\
Saamme siis jotain hyvin samanlaista kuin mitä saimme ensimmäisen reunaehdon soveltamisen jälkeen. Koska oletamme, että \(\lambda > 0\) tämä kertoo, että joko \(\sin \left( {\pi \sqrt \lambda } \right) = 0\) tai \({c_1} = 0\).
Huomaa kuitenkin, että jos \(\sin \left( {\pi \sqrt \lambda } \right) \ne 0\) niin meidän on oltava \({c_1} = {c_2} = 0\) ja saamme triviaalin ratkaisun. Meidän on siis vaadittava, että \(\sin \left( {\pi \sqrt \lambda } \right) = 0\), ja siten, aivan kuten olemme tehneet kahden edellisen esimerkin kohdalla, saamme nyt ominaissuureet,
\
Toteamalla, että \(\lambda > 0\) voimme nähdä, että meidän on aloitettava mahdollisten \(\(\n\)-arvojen luettelo nollan sijaan yhdestä.
Tiedämme nyt siis tämän tapauksen ominaisarvot, mutta entäpä ominaisfunktiot. Ratkaisu tietylle ominaisarvolle on,
\
ja meillä ei ole mitään syytä uskoa, että kumpikaan näistä kahdesta vakiosta olisi nolla tai nollasta poikkeava. Tällaisissa tapauksissa saamme kaksi sarjaa ominaisfunktioita, joista yksi vastaa kumpaakin vakiota. Tämän tapauksen kaksi ominaisfunktiosarjaa ovat,
\
Nyt toinen tapaus.
\(\underline {\lambda = 0} \)
Yleisratkaisu on,
\
Soveltamalla ensimmäistä reunaehtoa saadaan,
\
Yleisratkaisu on tällöin,
\
ja huomaa, että tämä tyydyttää triviaalisti toisen reunaehdon aivan kuten näimme edellä toisessa esimerkissä. Näin ollen meillä on jälleen \(\lambda = 0\) tämän BVP:n ominaisarvona ja tätä ominaisarvoa vastaava ominaisfunktio on,
\
Hoidetaan lopuksi kolmas tapaus.
\(\underline {\lambda < 0} \)
Yleisratkaisu tässä on,
\
Soveltamalla ensimmäistä reunaehtoa ja käyttämällä sitä tosiasiaa, että hyperbolinen kosini on parillinen ja hyperbolinen sini on pariton saadaan,
\
Tässä tapauksessa oletamme, että \(\lambda < 0\), joten tiedämme, että \(\pi \sqrt { – \lambda } \ne 0\), mikä puolestaan kertoo, että \(\sinh \left( {\pi \sqrt { – \lambda } \right) \ne 0\). Meidän on siis oltava \({c_2} = 0\).
Sovelletaan nyt toista reunaehtoa, jotta saadaan,
\
Oletuksemme \(\lambda \) perusteella meillä ei ole tässäkään tapauksessa muuta vaihtoehtoa kuin olla \({c_1} = 0\).
Siten tässä tapauksessa ainoa ratkaisu on triviaaliratkaisu, joten tälle BVP:lle meillä ei taaskaan ole negatiivisia ominaisarvoja.
Yhteenvetona meillä on siis seuraavat ominaisarvot/eigenfunktiot tälle BVP:lle.
\
Huomaa, että olemme tunnustaneet, että \(\lambda > 0\) kohdalla meillä oli kaksi sarjaa ominaisfunktioita luettelemalla ne kumpikin erikseen. Lisäksi voimme jälleen yhdistää kaksi viimeksi mainittua yhdeksi ominaisarvojen ja ominaisfunktioiden joukoksi. Näin tekemällä saadaan seuraava joukko ominaisarvoja ja ominaistoimintoja.
\
Jälleen kerran meillä on esimerkki, jossa ei ole negatiivisia ominaisarvoja. Emme voi tarpeeksi korostaa, että tämä riippuu enemmänkin differentiaaliyhtälöstä, jonka kanssa työskentelemme, kuin mistään muusta, ja tulee esimerkkejä, joissa saatamme saada negatiivisia ominaisarvoja.
Nyt olemme tähän asti työskennelleet vain yhden differentiaaliyhtälön kanssa, joten työstetään esimerkki eri differentiaaliyhtälöllä vain varmistaaksemme, ettemme lukkiudu liikaa tähän yhteen differentiaaliyhtälöön.
Ennen tämän esimerkin työstämistä huomioidaan, että työskentelemme edelleen suurimman osan esimerkeistämme sillä yhdellä differentiaaliyhtälöllä, jota olemme käyttäneet tähän asti. Työskentelemme tämän toisen differentiaaliyhtälön kanssa vain varmistaaksemme, ettemme lukkiudu liikaa yhden ainoan differentiaaliyhtälön käyttämiseen.
Tämä on Eulerin differentiaaliyhtälö, joten tiedämme, että meidän on löydettävä seuraavan neliöyhtälön juuret.
\
Tämän neliöyhtälön juuret ovat,
\
Nyt meillä on jälleen joitakin tapauksia, joiden kanssa voimme työskennellä, mutta ne eivät kuitenkaan ole samoja kuin aiemmissa esimerkeissä. Ratkaisu riippuu siitä, ovatko juuret reaalisia erillisiä, kaksinkertaisia vai kompleksisia, ja nämä tapaukset riippuvat \(1 – \lambda \) merkistä/arvosta. Käydään siis tapaukset läpi.
\(\underline {1 – \lambda < 0,\,\,\,\lambda > 1} \)
Tässä tapauksessa juuret ovat kompleksisia ja meidän on kirjoitettava ne seuraavasti, jotta voimme kirjoittaa ratkaisun.
\
Kirjoittamalla juuret tällä tavalla tiedämme, että \(\lambda – 1 > 0\) ja näin ollen \(\sqrt {\lambda – 1} \) on nyt reaaliluku, jota tarvitsemme kirjoittaaksemme seuraavan ratkaisun,
\
Soveltamalla ensimmäistä reunaehtoa saamme,
\
Toinen reunaehto antaa meille,
\
Välttääksemme triviaalin ratkaisun tässä tapauksessa vaadimme,
\
Tämä on paljon monimutkaisempi ehto kuin mitä olemme nähneet tähän asti, mutta muuten teemme saman asian. Ratkaisemalla \(\lambda \) saamme siis seuraavan joukon ominaisarvoja tälle tapaukselle.
\
Huomaa, että meidän on aloitettava \(n\):n lista ykkösestä eikä nollasta varmistaaksemme, että meillä on \(\lambda > 1\), kuten oletamme tässä tapauksessa.
Näitä ominaisarvoja vastaavat ominaisfunktiot ovat,
\
Nyt toinen tapaus.
\(\underline {1 – \lambda = 0,\,\,\,\,\,\lambda = 1} \)
Tässä tapauksessa saamme \:n kaksoisjuuren({r_{\,1,2}} = – 1\) ja näin ollen ratkaisu on,
\
Soveltamalla ensimmäistä reunaehtoa saadaan,
\
Toinen reunaehto antaa,
\
Meillä on siis vain triviaaliratkaisu tälle tapaukselle, joten \(\lambda = 1\) ei ole ominaisarvo.
Hoidetaan nyt kolmas (ja viimeinen) tapaus.
\(\underline {1 – \lambda > 0,\,\,\,\lambda < 1} \)
Tässä tapauksessa on kaksi reaalista erillistä juurta ja ratkaisu on,
\
Soveltamalla ensimmäistä reunaehtoa saadaan,
\
Käyttämällä tätä ratkaisustamme tulee,
\
Toisen reunaehdon soveltaminen antaa,
\
Nyt, koska tiedämme, että \(\lambda \ne 1\) tässä tapauksessa suluissa olevien kahden termin eksponentit eivät ole samat ja siten suluissa oleva termi ei ole nolla. Tämä tarkoittaa, että meillä voi olla vain,
\
ja niinpä tässä tapauksessa meillä on vain triviaaliratkaisu, eikä ole mitään ominaisarvoja, joille \(\lambda < 1\).
Tällöin tämän BVP:n ainoat ominaisarvot tulevat ensimmäisestä tapauksesta.
Olemme siis nyt työstäneet esimerkin, jossa käytetään muuta differentiaaliyhtälöä kuin tähän asti käyttämäämme ”tavallista”. Kuten näimme työssä, perusprosessi oli kuitenkin melko samanlainen. Totesimme, että oli olemassa useita tapauksia (tässä kolme, mutta ei aina kolme), jotka antoivat erilaisia ratkaisuja. Tarkastelimme jokaista tapausta selvittääksemme, olivatko ei-triviaalit ratkaisut mahdollisia, ja jos näin oli, löysimme kyseistä tapausta vastaavat ominaisarvot ja ominaistoiminnot.
Meidän täytyy työstää vielä yksi esimerkki tässä jaksossa ennen kuin jätämme tämän jakson uusien aiheiden pariin. Neljä esimerkkiä, joita olemme työstäneet tähän pisteeseen asti, olivat kaikki melko yksinkertaisia (yksinkertaisuus on tietysti suhteellista…), mutta emme kuitenkaan halua lähteä tunnustamatta, että monet itseisarvo-/eigenfunktio-ongelmat ovat niin helppoja.
Monissa esimerkeissä ei ole edes mahdollista saada täydellistä listaa BVP:n kaikista mahdollisista itseisarvoista. Usein yhtälöt, jotka meidän on ratkaistava ominaisarvojen saamiseksi, ovat vaikeita, ellei jopa mahdottomia ratkaista tarkasti. Tarkastellaan siis yhtä tällaista esimerkkiä, jotta nähdään, millaisia asioita voidaan tehdä, jotta saadaan ainakin käsitys siitä, miltä ominaisarvot näyttävät tällaisissa tapauksissa.
Tämän BVP:n reunaehdot ovat melko erilaiset kuin ne, joiden kanssa olemme työskennelleet tähän asti. Perusprosessi on kuitenkin sama. Aloitetaan siis ensimmäisestä tapauksesta.
\(\underline {\lambda > 0} \)
Differentiaaliyhtälön yleinen ratkaisu on identtinen ensimmäisten esimerkkien kanssa, joten meillä on,
\
Soveltamalla ensimmäistä reunaehtoa saamme,
\
Toisen reunaehdon avulla saamme,
\
Jos siis annamme \({c_2} = 0\), saamme triviaaliratkaisun, joten tämän reunaehdon täyttämiseksi meidän on sen sijaan vaadittava,
\
Nyt, tällä yhtälöllä on ratkaisut, mutta meidän on käytettävä joitakin numeerisia tekniikoita saadaksemme ne. Nähdäksemme, mistä tässä on kyse, piirretään \(\tan \left( \sqrt \lambda } \right)\) ja \( – \sqrt \lambda \) samaan kuvaajaan. Tässä on tuo kuvaaja ja huomaa, että vaaka-akselilla on oikeasti arvot \(\sqrt \lambda \), koska se helpottaa asioiden hahmottamista ja suhteuttamista meille tuttuihin arvoihin.

Tässä tapauksessa ominaisarvot esiintyvät siis kahden käyrän leikkauspisteessä. Olemme näyttäneet viisi ensimmäistä kuvaajassa, ja jälleen kerran se, mikä näkyy kuvaajassa, on todellisuudessa todellisen ominaisarvon neliöjuuri, kuten olemme huomanneet.
Mielenkiintoista tässä on huomata, että mitä kauempana kuvaajassa ollaan, sitä lähemmäs ominaissuureet tulevat tangentin asymptooseja, joten hyödynnämme tätä ja sanomme, että tarpeeksi suurilla \(n\) voimme approksimoida ominaissuureita tangentin asymptoottien (hyvin tunnetuilla) sijainneilla.
Kuinka suuri \(n\) arvo on ennen kuin alamme käyttää approksimaatiota riippuu siitä, kuinka paljon tarkkuutta haluamme, mutta koska tiedämme asymptoottien sijainnin ja \(n\):n kasvaessa approksimaation tarkkuus kasvaa, joten se on riittävän helppo tarkistaa tietylle tarkkuudelle.
Tässä esimerkissä löysimme viisi ensimmäistä numeerisesti ja sitten käytämme approksimaatiota lopuille ominaissuureille. Tässä ovat nämä arvot/approksimaatiot.
\
Viiden ensimmäisen jälkeen suluissa oleva luku on asymptootin likiarvo. Kuten näemme, ne ovat hieman pielessä, mutta kun pääsemme arvoon \(n = 5\), approksimaation virhe on 0,9862 %. Virhe on siis alle 1 %, kun päästään arvoon \(n = 5\), ja se paranee vain, kun \(n\) arvo on suurempi.
Tämän tapauksen ominaistoiminnot ovat,
\
jossa \(\(\lambda _{\,n}}\):n arvot on annettu edellä.
Nyt sitten, kun tämä työ on tehty, tarkastellaan toista tapausta.
\(\underline {\lambda = 0} \)
Yleisratkaisu on,
\
Soveltamalla ensimmäistä reunaehtoa saadaan,
\
Käyttämällä tätä yleisratkaisu on sitten,
\
Soveltamalla tähän toista reunaehtoa saadaan,
\
Tässä tapauksessa saadaan siis vain triviaaliratkaisu, joten \(\lambda = 0\) ei ole ominaisarvo. Huomaa kuitenkin, että jos toinen reunaehto olisi ollut \(y’\left( 1 \right) – y\left( 1 \right) = 0\), niin \(\lambda = 0\) olisi ollut itseisarvo (jossa olisi ollut ominaistoiminnot \(y\left( x \right) = x\)), joten tässäkin tapauksessa on varottava lukemasta liikaa tähän työhömme.
Huolehditaan lopuksi kolmannesta tapauksesta.
\(\underline {\lambda < 0} \)
Yleisratkaisu tässä on,
\
Soveltamalla ensimmäistä reunaehtoa saadaan,
\
Käyttämällä tätä yleisratkaisuksi tulee,
\
Soveltamalla tähän toista reunaehtoa saadaan,
\
Nyt oletuksesta tiedämme, että \(\lambda < 0\) ja siten \(\sqrt { – \lambda } > 0\). Tämä puolestaan kertoo, että \(\sinh \left( {\sqrt { – \lambda } } \right) > 0\) ja tiedämme, että \(\cosh \left( x \right) > 0\) kaikille \(x\). Näin ollen
\
ja näin ollen meidän on oltava \({c_2} = 0\) ja jälleen kerran tässä kolmannessa tapauksessa saamme triviaaliratkaisun ja näin ollen tällä BVP:llä ei ole negatiivisia ominaisarvoja.
Yhteenvetona voidaan todeta, että tämän BVP:n ainoat ominaisarvot saadaan olettamalla, että \(\lambda > 0\) ja ne on annettu edellä.
Olemme siis käsitelleet useita esimerkkejä ominaisarvoista/eigenfunktioista tässä osassa. Ennen kuin lähdemme tästä osiosta, meidän on vielä kerran todettava, että on olemassa valtava määrä erilaisia ongelmia, joita voimme työstää tässä, ja olemme oikeastaan näyttäneet vain kourallisen esimerkkejä, joten älkää lähdettäkö tästä osiosta pois siinä uskossa, että olemme näyttäneet teille kaiken.
Koko tämän osion tarkoitus on valmistella meitä seuraavassa luvussa esiintyviin ongelmatyyppeihin. Lisäksi seuraavassa luvussa rajoitumme jälleen melko perusluonteisiin ja yksinkertaisiin ongelmiin, jotta voimme havainnollistaa yhtä yleisimmistä osittaisdifferentiaaliyhtälöiden ratkaisumenetelmistä.
Leave a Reply