Bilineaarinen suodatus ja bilineaarinen interpolointi

Katso alla olevaa kuvaa. Pystytkö laskemaan arvot pisteissä A,B ja C?

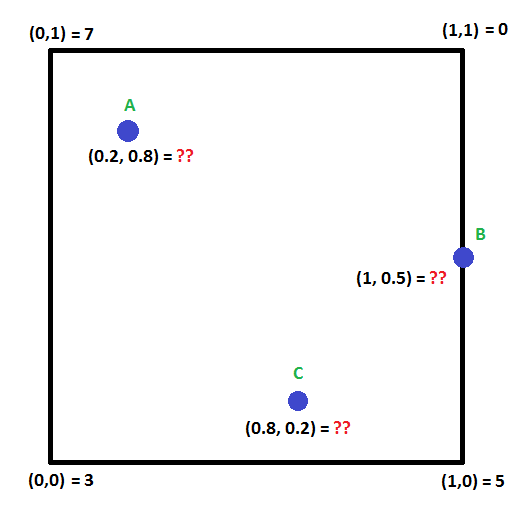
Tähän on olemassa tekniikka nimeltä bilineaarinen interpolointi, joka laajentaa lineaarisen interpoloinnin idean kahteen ulottuvuuteen.

Bilineaarisen interpoloinnin laskemiseksi teet vain lineaarisen interpoloinnin yhdellä akselilla ja sitten toisella.

Katso nämä esimerkit:

Piste A
Pisteen A koordinaatti on (0.2,0.8). Aloitetaan X-akselista.

Aluksi tehdään interpolointi neliön yläreunan yli X-akselilla. Se tarkoittaa, että meidän on kuljettava 0,2 (20 %) matkasta 7:stä 0:aan. Tuo 0,2 on x-akselin koordinaattimme. Laskemme sen seuraavasti:
7 + (0-7) * 0.2 = 5.6

Seuraavaksi teemme interpoloinnin neliön alareunan poikki X-akselilla. Samoin kuin edellä, siirrymme 0,2 (20 %) matkasta 3:sta 5:een. Tämän laskemiseksi teemme näin:
3 + (5-3) * 0.2 = 3.4

Nyt kun olemme interpoloineet X-akselin poikki, meidän on interpoloitava Y-akselin poikki. Menemme nyt 0,8 (80 %) matkan alimmasta arvosta (arvo Y = 0) ylimpään arvoon (arvo Y = 1). Alin arvo on tekemämme alin interpolointi (3,4) ja ylin arvo on tekemämme ylin interpolointi (5,6).

Meidän on siis mentävä 0,8 (80 %) matkasta 3,4:stä 5,6:een. Sen laskemiseksi teemme näin:
3.4 + (5.6 – 3.4) * 0.8 = 5.16

Pisteen A arvo on siis 5.16. Alla olevan kuvan pitäisi auttaa selittämään visuaalisesti läpi käymäämme prosessia.

Piste B

Pisteen B koordinaatit ovat (1.0,0.5).

Aloitetaan taas X-akselin interpoloinnista (tosin voisit halutessasi helposti aloittaa ensin Y:stä! Pääsisit samaan lopputulokseen).

Tehdään X-akselin interpolointi ylhäällä, meidän on mentävä 1.0 (100 %) matkasta 7:stä 0:aan. Osaat varmasti arvata vastauksen, mutta tässä se on laskettu:
7 + (0-7) * 1.0 = 0

Tehdään vastaavasti X-akselin interpolointi alhaalla. Meidän on kuljettava 1,0 (100 %) matkasta 3:sta 5:een.
3 + (5-3) * 1,0 = 5

Seuraavaksi tulee Y-akselin interpolointi. Meidän on mentävä 0,5 (50 %) matkasta 5:stä 0:aan.
5 + (0-5) * 0,5 = 2,5

Tässä se on, arvo pisteessä B on 2,5. Tämänkin pitäisi käydä järkeen kaaviota katsomalla. Se on periaatteessa 1d lineaarinen interpolointi 5:n ja 0:n välillä ja on niiden puolivälissä, joten intuitiivisesti vastauksen 2.5 pitäisi olla järkevä.

Piste C

Pisteen C koordinaatti on (0.8,0.2).

Tehdään vielä kerran X-akselilla interpolointi laatikon yläreunan yli. Meidän on kuljettava 0,8 (80 %) matkasta 7:stä 0:aan.
7 + (0-7) * 0,8 = 1,4

Tehdään sitten X-akselin interpolointi laatikon alaosan poikki. Meidän on mentävä 0,8 (80 %) matkasta 3:sta 5:een.
3 + (5-3) * 0,8 = 4,6

Viimeiseksi y-akselin interpolointi. Meidän on mentävä 0,2 (20 %) 4,6:sta 1,4:ään.
4,6 + (1,4-4,6) * 0,2 = 3,96

Pisteen C arvo on 3.96

Bilineaarinen suodatus

Vaikka bilineaarinen interpolointi on hyödyllistä, jos sinulla on ruudukko dataa, jonka sisällä haluat interpoloida arvoja (kuten korkeuskenttä, joka edustaa maastoa?!), missä tämä todella loistaa pelinkehityksessä on bilineaarinen tekstuurien suodatus.

Periaatteessa, kun sinulla on tekstuurikoordinaatti, joka ei ole täydellisesti linjassa tekstuurin pikselin keskipisteen kanssa (koska siinä on jäännös), se käyttää koordinaatin murto-osaa tuon pikselin sisällä tehdäkseen bilineaarisen interpoloinnin neljän mukana olevan pikselin välillä lopullisen pikselin värin saamiseksi. Se tekee bilineaarisen interpoloinnin jokaiselle kanavalle:

Lopputulos on melko hyvä! Katso alla olevasta kuvasta, miten se toimii tekstuurissa, johon olemme zoomanneet liian pitkälle. Vasemmalla puolella käytetään bilineaarista suodatusta, kun taas oikealla puolella ei käytetä sitä, vaan näytetään vain lähin pikseli.

Johtuen siitä, että bilineaarisessa tekstuurisuodatuksessa on tehtävä neljä pikselilukua, jotta voidaan interpoloida pikselien välille, sen sijaan, että luettaisiin vain yksi pikseli, kuten silloin, kun tehdään lähimmän pikselin näytteenotto. Enemmän pikselilukuja = enemmän yleiskustannuksia, eikä käyttö ole yhtä halpaa (laskennallisesti).

Linkit

Jollekin tätä lukevalle tämä tieto on aika perusasia, ja saatat ihmetellä, miksi vaivauduin kirjoittamaan siitä. Katsokaa seuraavasta postauksesta jotain jotenkin outoa koskien bilineaarista suodatusta. Tätä tarvittiin ponnahduslautana seuraavaan asiaan, jonka haluan näyttää teille 😛

Wikipedia: Wikipedia: Lineaarinen interpolointi

Wikipedia: Bilineaarinen interpolointi

Wikipedia: Bilinear Filtering

The Dark Side of Bilinear Filtering

Katso nämä linkit saadaksesi syvempää tietoa laitteistopohjaisen bilineaarisen näytteenoton joistain puutteista (ja joistakin kiertotöistä):
iq: hardware interpolation
iq: improved texture interpolation