9.5 – Vaikuttavien datapisteiden tunnistaminen

Tässä osiossa opimme seuraavat kaksi toimenpidettä vaikuttavien datapisteiden tunnistamiseksi:

• Difference in Fits (DFFITS)
• Cookin etäisyydet

Kummankin toimenpiteen perusidea on sama, nimittäin se, että havainnot poistetaan yksitellen, ja joka kerta sovitetaan regressiomalli uudelleen jäljelle jääneille n-1 havainnolle. Sitten verrataan tuloksia, joissa käytetään kaikkia n havaintoa, tuloksiin, joista on poistettu i:nnen havainto, jotta nähdään, kuinka suuri vaikutus kyseisellä havainnolla on analyysiin. Näin analysoituna pystymme arvioimaan kunkin datapisteen mahdollisen vaikutuksen regressioanalyysiin.

Sovitusten ero (DFFITS)

Havainnon i sovitusten ero, jota merkitään nimellä DFFITSi, määritellään seuraavasti:

\

Kuten näet, osoittaja mittaa eroa ennustetuissa vasteissa, jotka saadaan, kun i:nnen datapiste otetaan mukaan analyysiin ja jätetään pois analyysistä. Nimittäjä on ennustettujen vastausten eron arvioitu keskihajonta. Näin ollen sovitusten ero kvantifioi niiden standardipoikkeamien lukumäärän, joiden verran sovitettu arvo muuttuu, kun i:nnen datapiste jätetään pois.

Havaintoa pidetään vaikuttavana, jos sen DFFITS-arvon absoluuttinen arvo on suurempi kuin:

\

joissa, kuten aina, n=havaintojen lukumäärä ja k=ennustetermejä (eli regressioparametrejä lukuun ottamatta leikkauspistettä). On tärkeää pitää mielessä, että tämä ei ole tiukka sääntö, vaan pikemminkin vain ohje! Ei ole vaikeaa löytää eri kirjoittajia, jotka käyttävät hieman erilaista ohjetta. Sen vuoksi suosin usein paljon subjektiivisempaa ohjetta, jonka mukaan datapistettä pidetään vaikutusvaltaisena, jos sen DFFITS-arvon absoluuttinen arvo erottuu muista DFFITS-arvoista kuin kipeä peukalo. Tämä on tietysti kvalitatiivinen arvio, ehkä niin kuin pitääkin, koska poikkeamat ovat luonteeltaan subjektiivisia suureita.

Esimerkki #2 (taas). Tarkistetaanpa eron sopivuusmitta tälle aineistolle (influence2.txt):

Regressoimalla y:n x:n suhteen ja pyytämällä difference in fits, saamme seuraavan ohjelmistotulosteen:

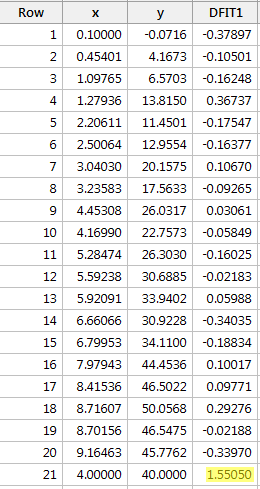
Käyttäen edellä määriteltyä objektiivista ohjetta pidämme datapistettä vaikuttavana, jos sen DFFITS-arvon absoluuttinen arvo on suurempi kuin:

\

Vain yhdellä datapisteellä – punaisella – on DFFITS-arvo, jonka absoluuttinen arvo (1.55050) on suurempi kuin 0,82. Tämän ohjeen perusteella pitäisimme siis punaista datapistettä vaikutusvaltaisena.

Esimerkki #3 (uudelleen). Tarkistetaanpa tämän datasarjan sovitusmitan ero (influence3.txt):

Regressoimalla y:n x:ään ja pyytämällä difference in fits -mittausta saamme seuraavan ohjelmistotulosteen:

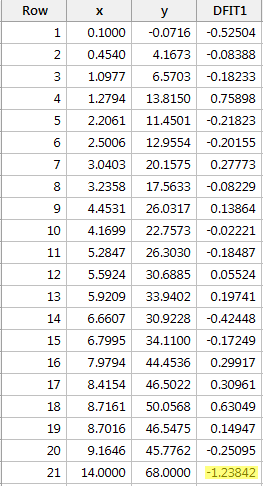
Käyttäen edellä määriteltyä objektiivista ohjetta pidämme datapistettä vaikuttavana, jos sen DFFITS-arvon absoluuttinen arvo on suurempi kuin:

\

Vain yhdellä datapisteellä – punaisella – on DFFITS-arvo, jonka absoluuttisen arvon absoluuttinen arvo (1.23841) on suurempi kuin 0,82. Tämän ohjeen perusteella pitäisimme siis punaista datapistettä vaikutusvaltaisena.

Kun tutkimme tätä datasarjaa tämän oppitunnin alussa, päätimme, että punainen datapiste ei vaikuta regressioanalyysiin kovinkaan paljon. Tässä tapauksessa ero sopivuusmitassa viittaa kuitenkin siihen, että se on todellakin vaikutusvaltainen. Mistä tässä on kyse? Kyse on siitä, että kaikki tämän oppitunnin toimenpiteet ovat vain välineitä, jotka merkitsevät data-analyytikolle mahdollisesti vaikuttavia datapisteitä. Loppujen lopuksi analyytikon olisi analysoitava tietokokonaisuus kahdesti – kerran merkittyjen datapisteiden kanssa ja kerran ilman niitä. Jos datapisteet muuttavat merkittävästi regressioanalyysin tulosta, tutkijan tulisi raportoida molempien analyysien tulokset.

Sattumoisin tässä esimerkissä tässä, jos käytämme subjektiivisempaa ohjetta siitä, erottuuko DFFITS-arvon absoluuttinen arvo kuin kipeä peukalo, emme todennäköisesti pidä punaista datapistettä vaikuttavana. Seuraavaksi suurin DFFITS-arvo (absoluuttisena arvona) on 0,75898. Tämä DFFITS-arvo ei poikkea kovinkaan paljon ”vaikutusvaltaisen” datapisteemme DFFITS-arvosta.

Esimerkki #4 (uudelleen). Tarkistetaanpa tämän datasarjan (influence4.txt):

Regressoimalla y:n x:ään ja pyytämällä difference in fits -mittausta saamme seuraavan ohjelmistotulosteen:

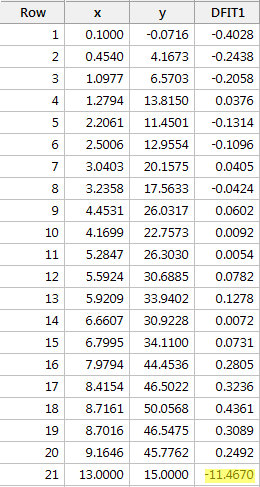
Käyttämällä edellä määriteltyä objektiivista ohjetta pidämme jälleen datapistettä vaikuttavana, jos sen DFFITS-arvon absoluuttinen arvo on suurempi kuin:

\

Mitä mieltä sinä olet? Pistääkö jokin DFFITS-arvo silmään kuin kipeä peukalo? Errr – punaisen datapisteen DFFITS-arvo (-11,4670 ) on varmasti eri suuruusluokkaa kuin kaikki muut. Tässä tapauksessa ei pitäisi olla epäilystäkään siitä, että punainen datapiste on vaikuttava!

Cookin etäisyys

Juuri tähän hyppäämällä, Cookin etäisyysmitta, jota merkitään Di, määritellään seuraavasti:

\.\.\]

Näyttää hiukan sotkuiselta, mutta tärkeintä on huomata, että Cookin Di on riippuvainen sekä residuaalista eistä, ei (ensimmäisessä termissä) että vipuvaikutuksesta, hii (toisessa termissä). Toisin sanoen sekä datapisteen x-arvolla että y-arvolla on merkitystä Cookin etäisyyden laskemisessa.

Lyhyesti:

• Di tiivistää suoraan, kuinka paljon kaikki sovitetut arvot muuttuvat, kun i:nnen havainto poistetaan.
• Datapiste, jolla on suuri Di, osoittaa, että kyseinen datapiste vaikuttaa voimakkaasti sovitettuihin arvoihin.

Tutkitaanpa, mitä tuo ensimmäinen väite tarkalleen ottaen tarkoittaa joidenkin esimerkkiemme yhteydessä.

Esimerkki nro 1 (uudelleen). Muistat ehkä, että näiden tietojen kuvaaja (influence1.txt) viittaa siihen, että tässä esimerkissä ei ole poikkeavia eikä vaikuttavia datapisteitä:

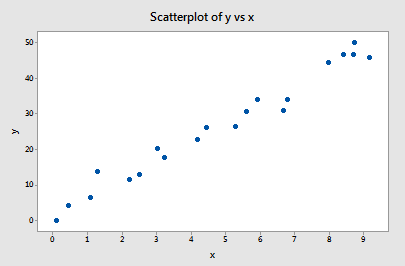
Jos regressoimme y:n suhteessa x:ään käyttäen kaikkia n = 20 datapistettä, havaitsemme, että estimoitu leikkauskerroin b0 = 1,732 ja estimoitu kaltevuuskerroin b1 = 5,117. Jos poistamme ensimmäisen datapisteen datasarjasta ja regressioimme y:n ja x:n välillä käyttäen jäljelle jääviä n = 19 datapistettä, havaitsemme, että estimoitu leikkauskerroin b0 = 1,732 ja estimoitu kaltevuuskerroin b1 = 5,1169. Kuten toivomme ja odotamme, estimaatit eivät muutu kovinkaan paljon, kun yksi datapiste poistetaan. Jatkamalla tätä prosessia, jossa kukin datapiste poistetaan yksi kerrallaan, ja piirtämällä tuloksena saadut estimoidut kaltevuudet (b1) suhteessa estimoituihin leikkauskertoimiin (b0) saadaan:

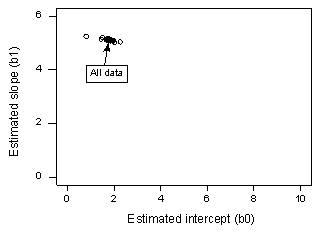
Ympärysmusta piste edustaa estimoituja kertoimia, jotka perustuvat kaikkiin n = 20 datapisteeseen. Avoimet ympyrät edustavat kutakin estimoitua kerrointa, jotka saadaan, kun jokainen datapiste poistetaan yksi kerrallaan. Kuten näet, estimoidut kertoimet ovat kaikki niputettu yhteen riippumatta siitä, mikä datapiste, jos mikä, poistetaan. Tämä viittaa siihen, että mikään datapiste ei vaikuta kohtuuttomasti estimoituun regressiofunktioon tai sovitettuihin arvoihin. Tässä tapauksessa odottaisimme kaikkien Cookin etäisyysmittojen, Di, olevan pieniä.

Esimerkki #4 (uudelleen). Muistat ehkä, että näiden tietojen kuvaaja (influence4.txt) viittaa siihen, että yksi datapiste on vaikutusvaltainen ja poikkeava tässä esimerkissä:

Jos regressoimme y:n suhteessa x:ään käyttäen kaikkia n = 21 datapistettä, havaitsemme, että estimoitu leikkauskerroin b0 = 8,51 ja estimoitu kaltevuuskerroin b1 = 3,32. Jos poistamme punaisen datapisteen aineistosta ja regressioimme y:n ja x:n välillä käyttäen jäljelle jääviä n = 20 datapistettä, havaitsemme, että estimoitu leikkauskerroin b0 = 1,732 ja estimoitu kaltevuuskerroin b1 = 5,1169. Wow-estimaatit muuttuvat huomattavasti, kun yksi datapiste poistetaan. Jatkamalla tätä prosessia, jossa jokainen datapiste poistetaan yksi kerrallaan, ja piirtämällä tuloksena saadut estimoidut kaltevuudet (b1) suhteessa estimoituihin leikkauskertoimiin (b0), saadaan:

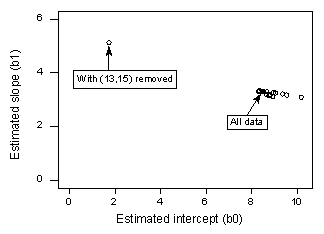
Jälleen yhtenäinen musta piste edustaa estimoituja kertoimia, jotka perustuvat kaikkiin n = 21 datapisteeseen. Avoimet ympyrät edustavat kutakin estimoitua kerrointa, jotka saadaan, kun jokainen datapiste poistetaan yksi kerrallaan. Kuten näet, punaista datapistettä (x = 13, y = 15) lukuun ottamatta estimoidut kertoimet ovat kaikki niputettu yhteen riippumatta siitä, mikä datapiste tai mikä tahansa datapiste poistetaan. Tämä viittaa siihen, että punainen datapiste on ainoa datapiste, joka vaikuttaa kohtuuttomasti estimoituun regressiofunktioon ja sitä kautta sovitettuihin arvoihin. Tässä tapauksessa odottaisimme, että punaisen datapisteen Cookin etäisyysmitta Di olisi suuri ja muiden datapisteiden Cookin etäisyysmitta Di pieni.

Käyttämällä Cookin etäisyysmittoja. Yllä olevien esimerkkien kauneus on siinä, että yksinkertaisten piirrosten avulla voidaan nähdä, mistä on kyse. Valitettavasti emme voi luottaa yksinkertaisiin piirroksiin moninkertaisen regression tapauksessa. Sen sijaan meidän on tukeuduttava ohjeisiin, joiden avulla päätämme, milloin Cookin etäisyysmitta on riittävän suuri, jotta datapistettä on syytä pitää vaikutusvaltaisena.

Tässä ovat yleisesti käytetyt ohjeet:

• Jos Di on suurempi kuin 0,5, i:nnen datapisteen tutkimista kannattaa jatkaa, sillä se saattaa olla vaikutusvaltainen.
• Jos Di on suurempi kuin 1, niin i:nnen datapisteen vaikutus on melko todennäköinen.
• Tai jos Di erottuu kuin kipeä peukalo muista Di-arvoista, se on lähes varmasti vaikutusvaltainen.

Esimerkki #2 (taas). Tarkistetaan Cookin etäisyysmitta tälle aineistolle (influence2.txt):

Regressoimalla y:n suhteessa x:ään ja pyytämällä Cookin etäisyysmittoja saamme seuraavan ohjelmistotulosteen:

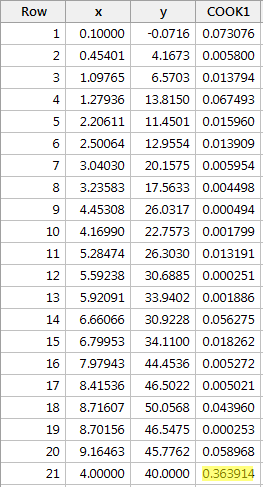
Punaisen datapisteen Cookin etäisyysmitta (0.363914) erottuu hieman muista Cookin etäisyysmitoista. Silti punaisen datapisteen Cookin etäisyysmitta on alle 0,5. Siksi Cookin etäisyysmitan perusteella emme luokittelisi punaista datapistettä vaikutusvaltaiseksi.

Esimerkki 3 (uudelleen). Tarkistetaan Cookin etäisyysmitta tälle datajoukolle (influence3.txt):

Regressoimalla y:n suhteessa x:ään ja pyytämällä Cookin etäisyysmittoja saamme seuraavan ohjelmistotulosteen:

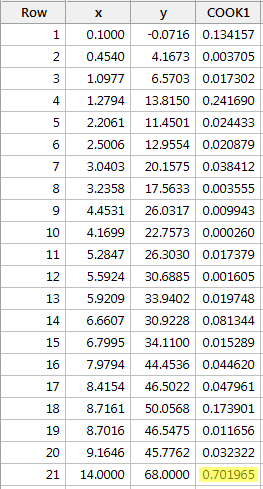
Punaisen datapisteen Cookin etäisyysmitta (0,701965) erottuu hieman muista Cookin etäisyysmitoista. Silti punaisen datapisteen Cookin etäisyysmitta on suurempi kuin 0,5 mutta pienempi kuin 1. Siksi Cookin etäisyysmitan perusteella voisimme ehkä tutkia asiaa tarkemmin, mutta emme välttämättä luokittelisi punaista datapistettä vaikutusvaltaiseksi.

Esimerkki #4 (uudelleen). Tarkistetaan Cookin etäisyysmitta tälle aineistolle (influence4.txt):

Regressoimalla y:n suhteessa x:ään ja pyytämällä Cookin etäisyysmittaa saamme seuraavan ohjelmistotulosteen:

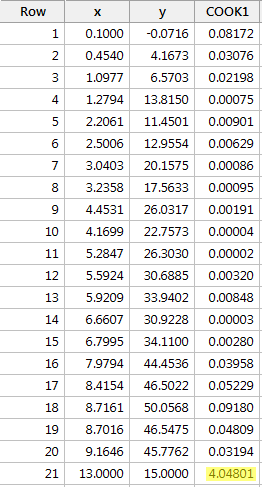
Tässä tapauksessa Cookin etäisyysmitta punaiselle datapisteelle (4.04801) erottuu huomattavasti muista Cookin etäisyysmitoista. Lisäksi punaisen datapisteen Cookin etäisyysmitta on suurempi kuin 1. Siksi Cookin etäisyysmitan perusteella – eikä yllättäen – luokittelisimme punaisen datapisteen vaikutusvaltaiseksi.

Vaihtoehtoinen Cookin etäisyyden tulkintamenetelmä, jota joskus käytetään, on suhteuttaa mitta F(k+1, n-k-1)-jakaumaan ja löytää sitä vastaava prosenttiluku. Jos tämä persentiili on pienempi kuin noin 10 tai 20 prosenttia, tapauksella ei ole juurikaan ilmeistä vaikutusta sovitettuihin arvoihin. Toisaalta, jos se on lähellä 50 prosenttia tai jopa suurempi, tapauksella on suuri vaikutus. (Kaikki ”siltä väliltä” on epäselvempää.)