Una suave introducción al problema de los cascos convexos

Los cascos convexos suelen ser útiles en muchos campos diferentes, a veces de forma bastante inesperada. En este artículo, explicaré la idea básica de los cascos convexos 2d y cómo utilizar el barrido de graham para encontrarlos. Así que si usted ya sabe acerca de la exploración de Graham, entonces este artículo no es para usted, pero si no, esto debería familiarizarse con algunos de los conceptos relevantes.

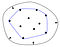
El casco convexo de un conjunto de puntos se define como el polígono convexo más pequeño, que encierra todos los puntos en el conjunto. Convexo significa que el polígono no tiene ninguna esquina doblada hacia dentro.

Las aristas rojas del polígono de la derecha encierran la esquina donde la forma es cóncava, lo contrario de convexa.

Una forma útil de pensar en el casco convexo es la analogía de la banda elástica. Supongamos que los puntos del conjunto son clavos, que sobresalen de una superficie plana. Imagina ahora lo que pasaría si coges una goma elástica y la estiras alrededor de los clavos. Al tratar de contraerse hasta su longitud original, la banda elástica encerraría los clavos, tocando los que sobresalen más del centro.

Para representar el casco convexo resultante en código, solemos almacenar la lista de puntos que sostienen esta banda elástica, es decir, la lista de puntos del casco convexo.

Nótese que todavía tenemos que definir qué debe ocurrir si tres puntos se encuentran en la misma línea. Si imaginamos que la goma elástica tiene un punto en el que toca uno de los clavos, pero no se dobla allí en absoluto, eso significa que el clavo allí se encuentra en una línea recta entre otros dos clavos. Dependiendo del problema, podríamos considerar que este clavo a lo largo de la recta forma parte de la salida, ya que toca la goma. Por otro lado, también podríamos decir que este clavo no debería formar parte de la salida, porque la forma de la goma elástica no cambia cuando la quitamos. Esta decisión depende del problema en el que se esté trabajando, y lo mejor de todo es que si se tiene una entrada en la que no hay tres puntos colineales (suele ser el caso en tareas fáciles para concursos de programación) entonces se puede incluso ignorar completamente este problema.

Hallar el casco convexo

Mirando un conjunto de puntos, la intuición humana nos permite averiguar rápidamente qué puntos es probable que toquen el casco convexo, y cuáles estarán más cerca del centro y, por tanto, alejados del casco convexo. Pero traducir esta intuición en código requiere un poco de trabajo.

Para encontrar el casco convexo de un conjunto de puntos, podemos utilizar un algoritmo llamado Graham Scan, que se considera uno de los primeros algoritmos de la geometría computacional. Usando este algoritmo, podemos encontrar el subconjunto de puntos que se encuentran en el casco convexo, junto con el orden en el que se encuentran estos puntos al recorrer el casco convexo.

El algoritmo comienza con la búsqueda de un punto, que sabemos que se encuentra en el casco convexo con seguridad. El punto con la coordenada y más baja, por ejemplo, puede considerarse una elección segura. Si existen varios puntos en la misma coordenada y, tomamos el que tiene la mayor coordenada x (esto también funciona con otros puntos de esquina, por ejemplo, primero la menor x y luego la menor y).

A continuación, ordenamos los demás puntos por el ángulo en el que se encuentran desde el punto de partida. Si dos puntos se encuentran en el mismo ángulo, el punto que está más cerca del punto de partida debería aparecer antes en la ordenación.

Ahora, la idea del algoritmo es recorrer esta matriz ordenada, determinando para cada punto, si se encuentra o no en el casco convexo. Esto significa que para cada triplete de puntos que encontramos, decidimos si forman una esquina convexa o cóncava. Si la esquina es cóncava, entonces sabemos que el punto central de este triplete no puede estar en el casco convexo.

(Nótese que los términos esquina cóncava y convexa tienen que usarse en relación con todo el polígono, sólo una esquina por sí misma no puede ser convexa o cóncava, ya que no habría dirección de referencia.)

Guardamos los puntos que se encuentran en el casco convexo en una pila, de esa forma podemos añadir puntos si llegamos a ellos en nuestro recorrido por los puntos ordenados, y eliminarlos si descubrimos que forman una esquina cóncava.

(Estrictamente hablando, tenemos que acceder a los dos puntos superiores de la pila, por lo que usamos un std::vector en su lugar, pero pensamos en él como una especie de pila, porque siempre nos preocupan sólo el par de elementos superiores.)

Al recorrer la matriz ordenada de puntos, añadimos el punto a la pila, y si más tarde encontramos que el punto no pertenece al casco convexo, lo eliminamos.

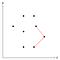
Podemos medir si la esquina actual se curva hacia dentro o hacia fuera calculando el producto cruzado y comprobando si es positivo o negativo. La figura anterior muestra un triplete de puntos en el que la esquina que forman es convexa, por lo que el del medio de estos tres puntos se queda en la pila por ahora.

Pasando al siguiente punto, seguimos haciendo lo mismo: comprobar si la esquina es convexa y si no lo es, eliminar el punto. Luego seguimos añadiendo el siguiente punto y repetimos.

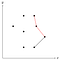
Esta esquina marcada en rojo es cóncava, por lo tanto eliminamos el punto del medio de la pila ya que no puede formar parte del casco convexo.

¿Cómo sabemos que esto nos dará la respuesta correcta?

Escribir una prueba rigurosa está fuera del alcance de este artículo, pero puedo escribir las ideas básicas. Sin embargo, te animo a que sigas e intentes rellenar los huecos.

Dado que hemos calculado el producto cruz en cada esquina, sabemos con seguridad que estamos obteniendo un polígono convexo. Ahora sólo tenemos que demostrar que este polígono convexo realmente encierra todos los puntos.

(En realidad, también habría que demostrar que éste es el polígono convexo más pequeño posible que satisface estas condiciones, pero eso se deduce fácilmente de que los puntos de las esquinas de nuestro polígono convexo son un subconjunto del conjunto original de puntos.)

Supongamos que existe un punto P fuera del polígono que acabamos de encontrar.

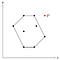
Dado que cada punto ha sido añadido a la pila una vez, sabemos que P fue eliminado de la pila en algún momento. Esto significa, que P, junto con sus puntos vecinos, llamémoslos O y Q, formaba una esquina cóncava.

Dado que O y Q se encuentran dentro del polígono (o en su frontera), P tendría que estar también dentro de la frontera, porque el polígono es convexo y la esquina que O y Q forman con P es cóncava con respecto al polígono.

Por tanto, hemos encontrado una contradicción, que significa que dicho punto P no puede existir.

Implementación

La implementación aquí proporcionada tiene una función convex_hull, que toma un std::vector que contiene los puntos como std::pairs de ints y devuelve otro std::vector que contiene los puntos que se encuentran en el casco convexo.

Análisis del tiempo de ejecución y de la memoria

Siempre es útil pensar en los algoritmos de complejidad en términos de la notación Big-O, que no voy a explicar aquí, porque Michael Olorunnisola aquí ya ha hecho un trabajo mucho mejor explicando que yo probablemente lo haría:

La clasificación de los puntos inicialmente toma O(n log n) tiempo, pero después de eso, cada paso se puede calcular en tiempo constante. Cada punto se añade y se quita de la pila como máximo una vez, lo que significa que el tiempo de ejecución en el peor de los casos es O(n log n).

El uso de la memoria, que es O(n) en este momento, podría optimizarse eliminando la necesidad de la pila y realizando las operaciones directamente en la matriz de entrada. Podríamos mover los puntos que se encuentran en el casco convexo al principio de la matriz de entrada y organizarlos en el orden correcto, y los otros puntos se moverían al resto de la matriz. La función podría entonces devolver una sola variable entera que denote la cantidad de puntos de la matriz que se encuentran en el casco convexo. Esto, por supuesto, tiene la desventaja de que la función se vuelve mucho más complicada, por lo que yo aconsejaría no hacerlo, a menos que estés codificando para sistemas embebidos o tengas problemas de memoria similares. Para la mayoría de las situaciones, la probabilidad de error / ahorro de memoria no vale la pena.

Otros Algoritmos

Una alternativa al Graham Scan es el algoritmo de Chan, que se basa en la misma idea, pero es más fácil de implementar. Sin embargo, tiene sentido entender primero cómo funciona el Graham Scan.

Si te sientes realmente elegante y quieres abordar el problema en tres dimensiones, echa un vistazo al algoritmo de Preparata y Hong introducido en su artículo de 1977 «Convex Hulls of Finite Sets of Points in Two and Three Dimensions».