Una breve introducción a la privacidad diferencial
Aaruran Elamurugaiyan
La privacidad puede cuantificarse. Mejor aún, podemos clasificar las estrategias que preservan la privacidad y decir cuál es más eficaz. Mejor aún, podemos diseñar estrategias que sean robustas incluso contra los hackers que tienen información auxiliar. Y por si fuera poco, podemos hacer todas estas cosas simultáneamente. Estas soluciones, y otras más, residen en una teoría probabilística llamada privacidad diferencial.
Este es el contexto. Estamos conservando (o gestionando) una base de datos sensible y nos gustaría hacer públicas algunas estadísticas de estos datos. Sin embargo, tenemos que asegurarnos de que es imposible que un adversario haga ingeniería inversa de los datos sensibles a partir de lo que hemos liberado . Un adversario en este caso es una parte con la intención de revelar, o conocer, al menos algunos de nuestros datos sensibles. La privacidad diferencial puede resolver los problemas que surgen cuando están presentes estos tres ingredientes: datos sensibles, conservadores que necesitan publicar estadísticas y adversarios que quieren recuperar los datos sensibles (véase la figura 1). Esta ingeniería inversa es un tipo de violación de la privacidad.

¿Pero qué tan difícil es violar la privacidad? No bastaría con anonimizar los datos? Si tienes información auxiliar de otras fuentes de datos, la anonimización no es suficiente. Por ejemplo, en 2007, Netflix publicó un conjunto de datos de sus valoraciones de usuarios como parte de una competición para ver si alguien podía superar su algoritmo de filtrado colaborativo. El conjunto de datos no contenía información de identificación personal, pero aun así los investigadores pudieron violar la privacidad; recuperaron el 99% de toda la información personal que se eliminó del conjunto de datos. En este caso, los investigadores violaron la privacidad utilizando información auxiliar de IMDB.
¿Cómo puede alguien defenderse de un adversario que tiene ayuda desconocida, y posiblemente ilimitada, del mundo exterior? La privacidad diferencial ofrece una solución. Los algoritmos diferencialmente privados son resistentes a los ataques adaptativos que utilizan información auxiliar . Estos algoritmos se basan en la incorporación de ruido aleatorio en la mezcla para que todo lo que recibe un adversario se vuelva ruidoso e impreciso, y así sea mucho más difícil violar la privacidad (si es que es factible).
Cuento ruidoso
Veamos un ejemplo sencillo de inyección de ruido. Supongamos que manejamos una base de datos de calificaciones crediticias (resumida por la Tabla 1).
Para este ejemplo, supongamos que el adversario quiere saber el número de personas que tienen una mala calificación crediticia (que es 3). Los datos son sensibles, por lo que no podemos revelar la verdad de base. En su lugar, utilizaremos un algoritmo que devuelva la verdad básica, N = 3, más algo de ruido aleatorio. Esta idea básica (añadir ruido aleatorio a la verdad básica) es la clave de la privacidad diferencial. Digamos que elegimos un número aleatorio L de una distribución de Laplace centrada en cero con una desviación estándar de 2. Devolvemos N+L. Explicaremos la elección de la desviación estándar en unos párrafos. (Si no ha oído hablar de la distribución de Laplace, vea la figura 2). Llamaremos a este algoritmo «recuento ruidoso».
Si vamos a informar de una respuesta disparatada y ruidosa, ¿qué sentido tiene este algoritmo? La respuesta es que nos permite alcanzar un equilibrio entre utilidad y privacidad. Queremos que el público en general obtenga alguna utilidad de nuestra base de datos, sin exponer ningún dato sensible a un posible adversario.
¿Qué recibiría realmente el adversario? Las respuestas se recogen en la Tabla 2.

La primera respuesta que recibe el adversario se aproxima, pero no es igual, a la verdad de base. En ese sentido, se engaña al adversario, se le proporciona utilidad y se protege la privacidad. Pero después de múltiples intentos, será capaz de estimar la verdad fundamental. Esta «estimación a partir de consultas repetidas» es una de las limitaciones fundamentales de la privacidad diferencial . Si el adversario puede realizar suficientes consultas a una base de datos con privacidad diferencial, podrá estimar los datos sensibles. En otras palabras, con más y más consultas, la privacidad se rompe. La tabla 2 demuestra empíricamente esta violación de la privacidad. Sin embargo, como se puede ver, el intervalo de confianza del 90% de estas 5 consultas es bastante amplio; la estimación no es muy precisa todavía.
¿Qué precisión puede tener esa estimación? Eche un vistazo a la figura 3, donde hemos realizado una simulación varias veces y hemos representado los resultados.

Cada línea vertical ilustra la anchura de un intervalo de confianza del 95%, y los puntos indican la media de los datos muestreados del adversario. Obsérvese que estos gráficos tienen un eje horizontal logarítmico y que el ruido se extrae de variables aleatorias de Laplace independientes e idénticamente distribuidas. En general, la media es más ruidosa con menos consultas (ya que el tamaño de las muestras es pequeño). Como era de esperar, los intervalos de confianza se estrechan a medida que el adversario realiza más consultas (ya que el tamaño de la muestra aumenta, y el ruido se promedia a cero). Sólo con inspeccionar el gráfico, podemos ver que se necesitan unas 50 consultas para hacer una estimación decente.
Reflexionemos sobre ese ejemplo. En primer lugar, al añadir ruido aleatorio, hemos hecho más difícil que un adversario vulnere la privacidad. En segundo lugar, la estrategia de ocultación que empleamos era sencilla de implementar y entender. Desgraciadamente, con más y más consultas, el adversario fue capaz de aproximarse al verdadero recuento.
Si aumentamos la varianza del ruido añadido, podemos defender mejor nuestros datos, pero no podemos simplemente añadir cualquier ruido de Laplace a una función que queremos ocultar. La razón es que la cantidad de ruido que debemos añadir depende de la sensibilidad de la función, y cada función tiene su propia sensibilidad. En particular, la función de recuento tiene una sensibilidad de 1. Veamos qué significa la sensibilidad en este contexto.
La sensibilidad y el mecanismo de Laplace
Para una función:
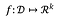
la sensibilidad de f es:
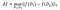
en los conjuntos de datos D₁, D₂ que difieren como máximo en un elemento .
La definición anterior es bastante matemática, pero no es tan mala como parece. A grandes rasgos, la sensibilidad de una función es la mayor diferencia posible que una fila puede tener en el resultado de esa función, para cualquier conjunto de datos. Por ejemplo, en nuestro conjunto de datos de juguete, contar el número de filas tiene una sensibilidad de 1, porque añadir o eliminar una sola fila de cualquier conjunto de datos cambiará el recuento como máximo en 1.
Como otro ejemplo, supongamos que pensamos en «contar redondeado a un múltiplo de 5». Esta función tiene una sensibilidad de 5, y podemos demostrarlo muy fácilmente. Si tenemos dos conjuntos de datos de tamaño 10 y 11, difieren en una fila, pero los «recuentos redondeados a un múltiplo de 5» son 10 y 15 respectivamente. De hecho, cinco es la mayor diferencia posible que puede producir esta función de ejemplo. Por lo tanto, su sensibilidad es 5.
Calcular la sensibilidad para una función arbitraria es difícil. Se ha invertido una cantidad considerable de esfuerzo de investigación en la estimación de las sensibilidades , la mejora de las estimaciones de la sensibilidad y la elusión del cálculo de la sensibilidad.
¿Cómo se relaciona la sensibilidad con el recuento ruidoso? Nuestra estrategia de recuento ruidoso utilizó un algoritmo llamado mecanismo de Laplace, que a su vez se basa en la sensibilidad de la función que oscurece . En el Algoritmo 1, tenemos una implementación ingenua en pseudocódigo del mecanismo de Laplace .
Algoritmo 1
Input: Función F, Entrada X, Nivel de privacidad ϵ
Salida: Una respuesta ruidosa
Calcular F (X)
Calcular la sensibilidad de de F : S
Sacar el ruido L de una distribución de Laplace con varianza:
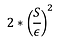
Devuelve F(X) + L
Cuanto mayor sea la sensibilidad S, más ruidosa será la respuesta. El recuento sólo tiene una sensibilidad de 1, así que no necesitamos añadir mucho ruido para preservar la privacidad.
Nota que el mecanismo de Laplace en el Algoritmo 1 consume un parámetro épsilon. Nos referiremos a esta cantidad como la pérdida de privacidad del mecanismo y forma parte de la definición más central en el campo de la privacidad diferencial: la privacidad diferencial epsilon. Para ilustrarlo, si recordamos nuestro ejemplo anterior y utilizamos un poco de álgebra, podemos ver que nuestro mecanismo de recuento ruidoso tiene una privacidad diferencial de épsilon, con un épsilon de 0,707. Al ajustar épsilon, controlamos el ruido de nuestro recuento ruidoso. Elegir un épsilon más pequeño produce resultados más ruidosos y mejores garantías de privacidad. Como referencia, Apple utiliza un épsilon de 2 en la autocorrección diferencialmente privada de su teclado.
La cantidad épsilon es la forma en que la privacidad diferencial puede proporcionar comparaciones rigurosas entre diferentes estrategias. La definición formal de la privacidad diferencial epsilon es un poco más involucrado matemáticamente, por lo que he omitido intencionalmente en esta entrada del blog. Puedes leer más sobre ello en el estudio de Dwork sobre la privacidad diferencial.
Como recuerdas, el ejemplo de recuento ruidoso tenía un épsilon de 0,707, que es bastante pequeño. Pero aún así violamos la privacidad después de 50 consultas. ¿Por qué? Porque con el aumento de las consultas, el presupuesto de privacidad crece, y por lo tanto la garantía de privacidad es peor.
El presupuesto de privacidad
En general, las pérdidas de privacidad se acumulan. Cuando se devuelven dos respuestas a un adversario, la pérdida total de privacidad es el doble, y la garantía de privacidad es la mitad de fuerte. Esta propiedad acumulativa es una consecuencia del teorema de la composición. En esencia, con cada nueva consulta, se libera información adicional sobre los datos sensibles. Por lo tanto, el teorema de la composición tiene una visión pesimista y asume el peor de los casos: la misma cantidad de fugas ocurre con cada nueva respuesta. Para obtener garantías sólidas de privacidad, queremos que la pérdida de privacidad sea pequeña. Así que en nuestro ejemplo, en el que tenemos una pérdida de privacidad de treinta y cinco (después de 50 consultas a nuestro mecanismo de conteo ruidoso de Laplace), la garantía de privacidad correspondiente es frágil.
¿Cómo funciona la privacidad diferencial si la pérdida de privacidad crece tan rápidamente? Para asegurar una garantía de privacidad significativa, los conservadores de datos pueden imponer una pérdida de privacidad máxima. Si el número de consultas supera el umbral, la garantía de privacidad se vuelve demasiado débil y el conservador deja de responder a las consultas. La pérdida máxima de privacidad se denomina presupuesto de privacidad. Podemos pensar en cada consulta como un «gasto» de privacidad que incurre en una pérdida de privacidad incremental. La estrategia de utilizar los presupuestos, los gastos y las pérdidas se conoce apropiadamente como contabilidad de la privacidad.
La contabilidad de la privacidad es una estrategia eficaz para calcular la pérdida de privacidad después de múltiples consultas, pero todavía puede incorporar el teorema de la composición. Como se ha señalado anteriormente, el teorema de la composición asume el peor de los casos. En otras palabras, existen mejores alternativas.
Aprendizaje profundo
El aprendizaje profundo es un subcampo del aprendizaje automático, que pertenece al entrenamiento de redes neuronales profundas (DNNs) para estimar funciones desconocidas . (En un nivel alto, una DNN es una secuencia de transformaciones afines y no lineales que mapean algún espacio n-dimensional a un espacio m-dimensional). Sus aplicaciones están muy extendidas y no es necesario repetirlas aquí. Exploraremos cómo entrenar una red neuronal profunda de forma privada.
Las redes neuronales profundas suelen entrenarse utilizando una variante del descenso de gradiente estocástico (SGD). Abadi et al. inventaron una versión que preserva la privacidad de este popular algoritmo, comúnmente conocido como «SGD privado» (o PSGD). La figura 4 ilustra la potencia de su novedosa técnica. Abadi et al. inventaron un nuevo enfoque: el contador de momentos. La idea básica del contador de momentos es acumular el gasto de privacidad enmarcando la pérdida de privacidad como una variable aleatoria, y utilizando sus funciones generadoras de momentos para comprender mejor la distribución de esa variable (de ahí el nombre) . Los detalles técnicos completos están fuera del alcance de una entrada de blog introductoria, pero le animamos a leer el documento original para aprender más.

Pensamientos finales
Hemos revisado la teoría de la privacidad diferencial y hemos visto cómo se puede utilizar para cuantificar la privacidad. Los ejemplos de este post muestran cómo se pueden aplicar las ideas fundamentales y la conexión entre la aplicación y la teoría. Es importante recordar que las garantías de privacidad se deterioran con el uso repetido, por lo que vale la pena pensar en cómo mitigarlo, ya sea con presupuestos de privacidad u otras estrategias. Puedes investigar el deterioro haciendo clic en esta frase y repitiendo nuestros experimentos. Todavía hay muchas preguntas que no se han respondido aquí y una gran cantidad de literatura para explorar – ver las referencias a continuación. Le animamos a seguir leyendo.
Cynthia Dwork. Privacidad diferencial: Un estudio de resultados. International Conference on Theory and Applications of Models of Computation, 2008.
Colaboradores de Wikipedia. Distribución de Laplace, julio de 2018.
Aaruran Elamurugaiyan. Plots demonstrating standard error of differentially private responses over number of queries, August 2018.
Benjamin I. P. Rubinstein and Francesco Alda. Privacidad diferencial aleatoria sin dolor con muestreo de sensibilidad. En 34th International Conference on Machine Learning (ICML’2017) , 2017.
Cynthia Dwork y Aaron Roth. Los fundamentos algorítmicos de la privacidad diferencial . Now Publ., 2014.
Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan Mcmahan, Ilya Mironov, Kunal Talwar y Li Zhang. Aprendizaje profundo con privacidad diferencial. Actas de la Conferencia ACM SIGSAC 2016 sobre seguridad informática y de las comunicaciones – CCS16 , 2016.
Frank D. McSherry. Consultas integradas de privacidad: Una plataforma extensible para el análisis de datos que preserva la privacidad. En Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data , SIGMOD ’09, páginas 19-30, Nueva York, NY, USA, 2009. ACM.
Colaboradores de Wikipedia. Aprendizaje profundo, agosto de 2018.
Leave a Reply