Resonancia de Helmholtz
- Análisis de la resonancia de Helmholtz
- Resonancia, impedancia, dependencia de la fase y de la frecuencia
- Complicaciones relacionadas con la longitud
- Resonancias de Helmholtz y guitarras
Análisis de la resonancia de Helmholtz
Ahora vamos a ser cuantitativos: En primer lugar, supondremos que la longitud de onda del sonido producido es mucho mayor que las dimensiones del resonador. En el caso de las botellas de la animación de la parte superior de esta página, las longitudes de onda son de 180 y 74 cm respectivamente, por lo que esta aproximación es bastante buena, pero conviene comprobarla siempre que se empiece a describir algo como un oscilador de Helmholtz. La consecuencia de esta aproximación es que podemos despreciar las variaciones de presión dentro del volumen del recipiente: la oscilación de la presión tendrá la misma fase en todas partes dentro del recipiente.
Dejemos que el aire en el cuello tenga una longitud efectiva L y un área de sección transversal S. Su masa es entonces SL veces la densidad del aire ρ. (Algunas complicaciones sobre la longitud efectiva se discuten al final de esta página). Si este «tapón» de aire desciende una pequeña distancia x dentro de la botella, comprime el aire del recipiente de forma que el aire que antes ocupaba el volumen V tiene ahora el volumen V – Sx. En consecuencia, la presión de ese aire aumenta desde la presión atmosférica PA hasta un valor superior PA + p.
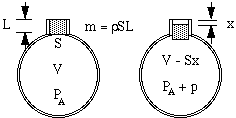
Ahora podrías pensar que el aumento de la presión sería simplemente proporcional a la disminución del volumen. Ese sería el caso si la compresión ocurriera tan lentamente que la temperatura no cambiara. Sin embargo, en las vibraciones que dan lugar al sonido, los cambios son rápidos, por lo que la temperatura aumenta en la compresión, dando un cambio mayor en la presión. Técnicamente son adiabáticas, lo que significa que el calor no tiene tiempo para moverse, y la ecuación resultante implica una constante γ, la relación de calores específicos, que es aproximadamente 1,4 para el aire. (Esto se explica en un apéndice.) Como resultado, el cambio de presión p producido por un pequeño cambio de volumen ΔV es sólo
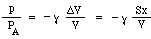
Ahora la masa m se mueve por la diferencia de presión entre la parte superior e inferior del cuello, es decir, una fuerza neta pS, por lo que escribimos la ley de Newton para la aceleración a:
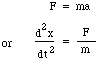
sustituyendo por F y m da: 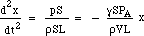
Así que la fuerza restauradora es proporcional al desplazamiento. Esta es la condición para el movimiento armónico simple, y tiene una frecuencia que es 1/2π veces la raíz cuadrada de la constante de proporcionalidad, por lo que
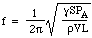
Ahora la velocidad c del sonido en el aire está determinada por la densidad, la presión y la relación de calores específicos, por lo que podemos escribir:
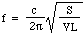
Pongamos algunos números: para una botella de 1 litro, con S = 3 centímetros cuadrados y L = 5 centímetros, la frecuencia es de 130 Hz, que es aproximadamente el Do por debajo del Do medio. (Ver notas.) Así que la longitud de onda es de 2,6 metros, que es mucho más grande que la botella. Esto justifica, post hoc, la suposición hecha al principio de la derivación.
Resonancia, impedancia, dependencia de la fase y de la frecuencia
Esta sección puede leerse por sí sola, pero si se quiere un fondo más detallado, ver Oscilaciones, Oscilaciones forzadas y Conformidad acústica, inercia e impedancia.
Volvamos a la representación mecánica y veamos el resonador de Helmholtz desde fuera, como se muestra en el primer esquema: estamos empujando con una fuerza oscilatoria F, con frecuencia f ,la masa m (el aire en el cuello del resonador), que se apoya en el muelle (el aire encerrado) con constante de muelle k, cuyo otro extremo está fijo (el aire en el resonador no puede escapar). De forma poco realista, despreciaremos la gravedad y el rozamiento (por ahora).
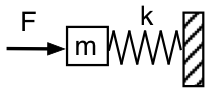
La fuerza necesaria para acelerar la masa es proporcional a la aceleración y, por tanto, proporcional a f2. A una frecuencia suficientemente baja, la fuerza necesaria para acelerar la masa es despreciable, por lo que F sólo tiene que comprimir y extender el muelle. Así que en ese límite, la fuerza aplicada F = +kx. (La fuerza del muelle es -kx.) La impedancia mecánica del sistema a esta baja frecuencia es complaciente o de muelle. Acústicamente, parece una conformidad acústica: empujamos la masa de aire en el cuello y comprimimos el aire en el resonador. La fuerza aplicada F a la derecha está en fase con x medida a la derecha, por lo que está 90° detrás de la velocidad y la presión aplicada está 90° detrás del flujo acústico en el resonador.
Recuerda que f2 depende de la aceleración. Así, a una frecuencia suficientemente alta, la fuerza del muelle es despreciable en comparación con la que acelera la masa. Por tanto, F está en fase con la aceleración, lo que la sitúa 90º por delante de la velocidad. Desde el punto de vista acústico, la presión aplicada está 90° por delante del flujo acústico en el resonador. Es una inercia mecánica o acústica.
En la frecuencia de resonancia (seguimos hablando del esquema anterior), la amplitud puede ser grande para una fuerza muy pequeña. Así que en la resonancia, la impedancia es muy baja, cuando se ve desde la fuerza aplicada a la masa desde el exterior (el diagrama de arriba). En la resonancia, hay un flujo máximo dentro y fuera del resonador.
Ahora considere lo que sucede si miramos la presión dentro del resonador (lejos del cuello). Aquí estamos mirando la fuerza en el resorte, por lo que nuestro análogo mecánico se parece a este esquema.
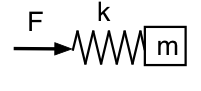
Esta vez, la baja frecuencia significa que la fuerza puede ser pequeña para una amplitud dada: el muelle y la masa se mueven juntos como una masa, y el sistema esta vez parece inercial a baja frecuencia. A alta frecuencia, la masa apenas se mueve, y el sistema es elástico o complaciente. Así que las relaciones de fase son opuestas a las que teníamos antes: a baja f, p adelanta a U en 90°; a alta f, p retrasa a U en 90°.
Complicaciones relacionadas con la longitud efectiva
El primer diagrama de esta página dibuja el «tapón» de aire como si fuera un cilindro que termina limpiamente en cualquier extremo del cuello de la botella. Esto es una simplificación excesiva. En la práctica, un volumen extra, tanto en el interior como en el exterior, se mueve con el aire en el cuello, como se sugiere en la animación anterior. La longitud extra que debe añadirse a la longitud geométrica del cuello es típicamente (y muy aproximadamente) de 0,6 veces el radio en el extremo exterior, y un radio en el extremo interior).
|
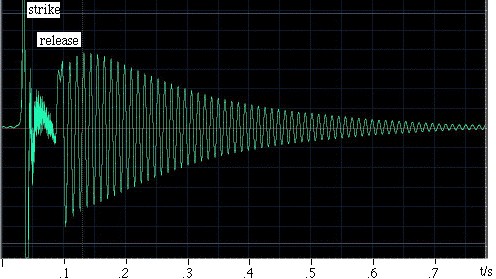
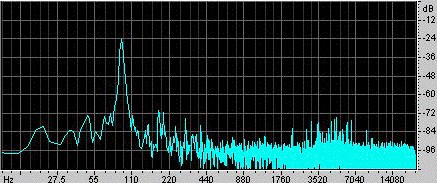
Un ejemplo. Ra Inta hizo este ejemplo. Tomó un resonador de Helmholtz esférico con un volumen de 0,00292 m3 y un cuello cilíndrico con una longitud de 0,080 m y un área de sección transversal de 0,00083 m2. Para excitarlo, lo golpea con la palma de la mano y luego lo suelta. Un micrófono situado en el interior del resonador registra el sonido, que se muestra en el oscilograma de la izquierda. Se puede ver que la mano sella el resonador durante bastante menos de 0,1 s, y que durante este tiempo las oscilaciones son más débiles y de frecuencia relativamente alta. Una vez que se suelta la mano, se establece una oscilación que desaparece gradualmente a medida que pierde energía por el arrastre viscoso y turbulento, y también por la radiación del sonido. Un examen minucioso muestra que la frecuencia aumenta ligeramente a medida que la mano se aleja del extremo abierto, ya que ésta restringe el ángulo sólido disponible para la radiación y, por tanto, aumenta el efecto del extremo (o corrección del extremo). La longitud del cuello se incrementa con un efecto final desviado y otro no desviado, lo que le da una longitud efectiva de 0,105 m. Con una velocidad del sonido de 343 m/s, la expresión anterior da una frecuencia de resonancia de 90 Hz. |
|
Resonancias de Helmholtz y guitarras
* He dicho más arriba que el aire del cuerpo de una guitarra actúa casi como un oscilador de Helmholtz. Este caso es complicado porque el cuerpo puede hincharse un poco cuando la presión del aire aumenta en su interior – y también porque el aire «en» la boca de la guitarra tiene una geometría que es menos fácil de visualizar que la del cuello de una botella. En efecto, en el caso del cuerpo de la guitarra, la longitud del tapón del aire es aproximadamente igual a los dos «efectos finales» del extremo de un «tubo» que sólo tiene un par de mm de grosor. Sin embargo, los efectos finales están relacionados y tienen un tamaño similar al radio del orificio, por lo que la masa de aire es considerable. La longitud del efecto final de un tubo cilíndrico que se abre a un bafle infinito y plano es 0,85 veces el radio del tubo. Aunque la caja de resonancia de una guitarra no es infinita, cabría esperar un efecto final similar, por lo que la longitud efectiva del «tapón» de aire sería aproximadamente 1,7 veces el radio del agujero. (Algunos fabricantes lo aumentan fijando un tubo corto debajo de la boca, con igual radio).
Un par de personas han escrito preguntando qué tamaño debe tener la boca para un instrumento determinado. Bien, podemos utilizar la ecuación anterior para empezar a responder a esa pregunta. Sin embargo, la hinchazón del cuerpo es importante. Esto hace que el «resorte» del aire sea más suave y, por lo tanto, disminuye la frecuencia. La resonancia puramente de Helmholtz puede investigarse manteniendo constante el volumen del cuerpo. Para medirla, una práctica habitual es enterrar la guitarra en arena, para impedir el hinchamiento o la «respiración» del cuerpo. Sin embargo, las guitarras no suelen tocarse en esta situación. Así que el cálculo de Helmholtz dará una sobreestimación de la frecuencia de resonancia para un cuerpo real y flexible.
Supongamos un orificio de sonido circular con radio r, por lo que S = πr2, y L = 1,7r como se ha explicado anteriormente. Cuando sustituimos en la ecuación de la frecuencia de Helmholtz, utilizando c = 340 m/s, obtenemos:
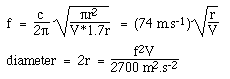
Observa que estamos utilizando unidades estándar del SI: hemos utilizado la velocidad del sonido en metros y segundos, por lo que el volumen debe estar en metros cúbicos y la frecuencia en Hertz, para dar una respuesta en metros.
Es más complicado cuando los agujeros del tono no son circulares, porque el efecto final no es igual al de un círculo con la misma área. El estudiante de doctorado y luthier John McLennan está escribiendo un informe de algunas mediciones sobre esto, que publicaremos aquí pronto.
En los instrumentos de la familia de la guitarra y el violín, la resonancia de Helmholtz (más el cuerpo) suele estar cerca o un poco por debajo de la frecuencia de la segunda cuerda más grave, alrededor de Re en un violín o Sol-A en una guitarra. Se puede reducir o desplazar la frecuencia de Helmholtz sustancialmente cubriendo todo o parte del agujero con un trozo de cartón rígido de forma adecuada. Si entonces tocas una nota cerca de la resonancia y luego deslizas la cartulina para que cubra y revele alternativamente el agujero, escucharás claramente el efecto de la resonancia.
¿Es razonable el efecto de 0,85r? Ra Inta, que hizo un doctorado sobre la acústica de la guitarra en nuestro laboratorio, sugiere una demostración interesante:
Ahumecta las cuerdas de tu guitarra para que no vibren (por ejemplo, un pañuelo entre las cuerdas y el diapasón). Mantenga la palma de una mano por encima de la boca, y cerca de ella. Con un dedo de la otra mano, golpea la caja de resonancia de forma brusca cerca de la boca y de la primera cuerda. Sentirá un pulso de aire en la palma de la mano. El golpe de tu dedo empuja la caja de resonancia hacia dentro y saca algo de aire del cuerpo. Ahora aleje su mano gradualmente del agujero y continúe golpeando con el dedo. ¿Cuándo deja de sentir el movimiento del aire? Esto te dará una estimación aproximada de la longitud del «efecto final» en el caso del agujero de sonido.
Sintonizando la resonancia de Helmholtz
Entre las publicaciones de John McLennan, estudiante de doctorado en este laboratorio, hay un artículo en el que varía la resonancia de Helmholtz variando la velocidad del sonido.
- McLennan, J.E. (2003) «Estudios A0 y A1 en el violín utilizando mezclas de CO2, He y aire/helio». Acustica, 89, 176-180.
Algunas fotos de resonadores históricos de Helmholtz proporcionadas por Thomas B. Greenslade, Kenyon College, Ohio.
Leave a Reply