¿Qué es la geometría analítica?
¿Qué es la geometría analítica?
La geometría analítica es una rama del álgebra que se utiliza para modelar objetos geométricos, siendo los puntos, las líneas (rectas) y los círculos los más básicos. La geometría analítica es un gran invento de Descartes y Fermat.
En la geometría analítica plana, los puntos se definen como pares ordenados de números, digamos, (x, y), mientras que las rectas se definen a su vez como los conjuntos de puntos que satisfacen ecuaciones lineales, véanse las excelentes exposiciones de D. Pedoe o D. Brannan et al. Desde el punto de vista de la geometría analítica, los axiomas geométricos son teoremas derivables. Por ejemplo, para dos puntos distintos (x1, y1) y (x2, y2), existe una única recta ax + by + c = 0 que pasa por estos puntos. Sus coeficientes a, b, c se pueden encontrar (hasta un factor constante) a partir del sistema lineal de dos ecuaciones
| ax1 + by1 + c = 0 ax2 + by2 + c = 0, |
o directamente de la ecuación del determinante
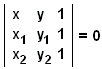 |
Sin embargo, ninguna teoría axiomática puede escapar de usar elementos indefinidos. En la Teoría de Conjuntos que subyace en gran parte de las matemáticas y, en particular, en la geometría analítica, la noción más fundamental de conjunto permanece indefinida.
La geometría del espacio tridimensional se modela con triples de números (x, y, z) y una ecuación lineal 3D ax + by + cz + d = 0 define un plano. En general, la geometría analítica proporciona una herramienta conveniente para trabajar en dimensiones superiores.
En el marco de la geometría analítica uno puede (y lo hace) modelar geometrías no euclidianas también. Por ejemplo, en la geometría proyectiva plana un punto es un triple de coordenadas homogéneas (x, y, z), no todas 0, tal que
| (tx, ty, tz) = (x, y, z), |
| ax + bx + cz = 0. |
En la geometría analítica, las secciones cónicas se definen mediante ecuaciones de segundo grado:
| ax² + bxy + cy² + dx + ey + f = 0. |
La parte de la geometría analítica que se ocupa principalmente de las ecuaciones lineales se llama Álgebra Lineal.
La geometría analítica cartesiana es la geometría en la que los ejes x = 0 e y = 0 son perpendiculares.
Las componentes de la n-tupla x = (x1, …, xn) se conocen como sus coordenadas. Cuando n = 2 o n = 3, la primera coordenada se llama abscisa y la segunda ordenada.
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
|Contacto||Página principal||Contenido||Geometría|Up|
Copyright © 1996-2018 Alexander Bogomolny
Leave a Reply