Prueba de Friedman en SPSS Statistics

SPSS Statistics

SPSS Statistics Output for the Friedman Test

SPSS Statistics generará dos o tres tablas, dependiendo de si ha seleccionado que se generen descriptivos y/o cuartiles además de ejecutar la prueba de Friedman.

Tabla de estadísticas descriptivas

Se producirá la tabla de estadísticas descriptivas si seleccionó la opción de cuartiles:

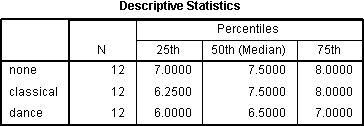
Publicada con permiso escrito de SPSS Statistics, IBM Corporation.

Esta es una tabla muy útil porque puede utilizarse para presentar estadísticas descriptivas en su sección de resultados para cada uno de los puntos de tiempo o condiciones (dependiendo de su diseño de estudio) para su variable dependiente. Esta utilidad se presentará en la sección «Presentación de los resultados» más adelante.

Tabla de rangos

La tabla de rangos muestra el rango medio para cada uno de los grupos relacionados, como se muestra a continuación:

Publicado con permiso escrito de SPSS Statistics, IBM Corporation.

La prueba de Friedman compara los rangos medios entre los grupos relacionados e indica cómo difieren los grupos, y se incluye por esta razón. Sin embargo, no es muy probable que informe de estos valores en la sección de resultados, sino que lo más probable es que informe del valor medio de cada grupo relacionado.

Tabla de estadísticas de la prueba

La tabla de estadísticas de la prueba le informa del resultado real de la prueba de Friedman, y de si hubo una diferencia general estadísticamente significativa entre los rangos medios de sus grupos relacionados. Para el ejemplo utilizado en esta guía, la tabla tiene el siguiente aspecto:

Publicada con el permiso escrito de SPSS Statistics, IBM Corporation.

La tabla anterior proporciona el valor del estadístico de la prueba (χ2) («Chi-cuadrado»), los grados de libertad («df») y el nivel de significación («Asymp. Sig.»), que es todo lo que necesitamos para informar del resultado de la prueba de Friedman. En nuestro ejemplo, podemos ver que existe una diferencia global estadísticamente significativa entre los rangos medios de los grupos relacionados. Es importante tener en cuenta que la prueba de Friedman es una prueba ómnibus, como su alternativa paramétrica; es decir, le dice si hay diferencias globales, pero no señala qué grupos en particular difieren entre sí. Para ello es necesario realizar pruebas post hoc, que se discutirán después de la siguiente sección.

Estadística SPSS

Informar del resultado de la prueba de Friedman (sin pruebas post hoc)

Puede informar del resultado de la prueba de Friedman de la siguiente manera:

También podría incluir los valores de la mediana para cada uno de los grupos relacionados. Sin embargo, en esta fase, sólo sabe que hay diferencias en alguna parte entre los grupos relacionados, pero no sabe exactamente dónde están esas diferencias. Recuerde, sin embargo, que si el resultado de la prueba de Friedman no fue estadísticamente significativo, no debe realizar pruebas post hoc.

Pruebas post hoc

Para examinar dónde se producen realmente las diferencias, debe realizar pruebas de rango con signo de Wilcoxon por separado en las diferentes combinaciones de grupos relacionados. Así, en este ejemplo, compararía las siguientes combinaciones:

• Nada a Clásico.
• Nada a Baile.
• Clásico a Baile.

Necesita utilizar un ajuste de Bonferroni en los resultados que obtenga de las pruebas de Wilcoxon porque está haciendo comparaciones múltiples, lo que hace más probable que declare un resultado significativo cuando no debería hacerlo (un error de Tipo I). Por suerte, el ajuste de Bonferroni es muy fácil de calcular; simplemente tome el nivel de significación que estaba utilizando inicialmente (en este caso, 0,05) y divídalo por el número de pruebas que está realizando. Así, en este ejemplo, tenemos un nuevo nivel de significación de 0,05/3 = 0,017. Esto significa que si el valor p es mayor que 0,017, no tenemos un resultado estadísticamente significativo.

Ejecutando estas pruebas (vea cómo con nuestra guía de la prueba de rangos con signo de Wilcoxon) en los resultados de este ejemplo, obtendrá el siguiente resultado:

Publicado con permiso escrito de SPSS Statistics, IBM Corporation.

Esta tabla muestra el resultado de la prueba de rango con signo de Wilcoxon en cada una de nuestras combinaciones. Es importante señalar que los valores de significación no se han ajustado en SPSS Statistics para compensar las comparaciones múltiples; debe comparar manualmente los valores de significación producidos por SPSS Statistics con el nivel de significación ajustado por Bonferroni que haya calculado. Podemos ver que en el nivel de significación p < 0,017, sólo el esfuerzo percibido entre la ausencia de música y la danza (danza-ninguna, p = 0,008) fue estadísticamente significativo.

Estadística SPSS

Informe del resultado de la prueba de Friedman (con pruebas post hoc)

Puede informar de los resultados de la prueba de Friedman con pruebas post hoc de la siguiente manera: