Articles /

Proceso de Gram-Schmidt

por Marco Taboga, PhD

El proceso (o procedimiento) de Gram-Schmidt es una secuencia de operaciones que permiten transformar un conjunto de vectores linealmente independientes en un conjunto de vectores ortonormales que abarcan el mismo espacio que abarca el conjunto original.

Tabla de contenidos

Preliminares

Revisemos algunas nociones esenciales para entender el proceso de Gram-Schmidt.

Recordemos que dos vectores $r$ y $s$ se dice que son ortogonales si y sólo si su producto interior es igual a cero, es decir,

Dado un producto interior, podemos definir la norma (longitud) de un vector $s$ como sigue:

Un conjunto de vectores se llama ortonormal si y sólo si sus elementos tienen norma unitaria y son ortogonales entre sí. En otras palabras, un conjunto de K vectores es ortonormal si y sólo si

Hemos demostrado que los vectores de un conjunto ortonormal son linealmente independientes.

Cuando una base para un espacio vectorial es también un conjunto ortonormal, se llama base ortonormal.

Proyecciones sobre conjuntos ortonormales

En el proceso de Gram-Schmidt, utilizamos repetidamente la siguiente proposición, que muestra que todo vector puede descomponerse en dos partes: 1) su proyección sobre un conjunto ortonormal y 2) un residuo que es ortogonal al conjunto ortonormal dado.

Proposición Sea $S$ un espacio vectorial equipado con un producto interior . Sea un conjunto ortonormal. Para cualquier $sin S$, tenemos donde $arepsilon _{S}$ es ortogonal a $u_{k}$ para cualquier $k=1,ldots ,K.$

Prueba

DefineEntonces, para cada $j=1,ldots ,K$, tenemos quedonde: en los pasos $rame{A}$ y $rame{B}$ hemos utilizado el hecho de que el producto interior es lineal en su primer argumento; en el paso $marco{C}$ hemos utilizado el hecho de que si $keq j$ ya que se trata de un conjunto ortonormal; en el paso $marco{D}$ hemos utilizado el hecho de que la norma de $u_{j}$ es igual a 1. Por tanto, $arepsilon _{S}$, tal y como se ha definido anteriormente, es ortogonal a todos los elementos del conjunto ortonormal, lo que demuestra la proposición.

El términose llama proyección lineal de $s$ sobre el conjunto ortonormal , mientras que el término $arepsilon _{S}$ se llama residuo de la proyección lineal.

Normalización

Otro hecho quizás obvio que vamos a utilizar repetidamente en el proceso de Gram-Schmidt es que, si tomamos cualquier vector distinto de cero y lo dividimos por su norma, entonces el resultado de la división es un nuevo vector que tiene norma unitaria.

En otras palabras, si entonces, por la propiedad de definición de la norma, tenemos que

Como consecuencia, podemos definiry, por la positividad y homogeneidad absoluta de la norma, tenemos

Resumen del procedimiento

Ahora que sabemos cómo normalizar un vector y cómo descomponerlo en una proyección sobre un conjunto ortonormal y un residuo, estamos preparados para explicar el procedimiento de Gram-Schmidt.

Vamos a proporcionar una visión general del proceso, después lo expresaremos formalmente como una proposición y discutiremos todos los detalles técnicos en la demostración de la proposición.

Aquí está la visión general.

Se nos da un conjunto de vectores linealmente independientes .

Para iniciar el proceso, normalizamos el primer vector, es decir, definimos

En el segundo paso, proyectamos $s_{2}$ sobre $u_{1}$:donde $arepsilon _{2}$ es el residuo de la proyección.

Entonces, normalizamos el residuo:

Después demostraremos que (para que se pueda realizar la normalización) porque los vectores de partida son linealmente independientes.

Los dos vectores $u_{1}$ y $u_{2}$ así obtenidos son ortonormales.

En el tercer paso, proyectamos $s_{3}$ sobre $u_{1}$ y $u_{2}$: y calculamos el residuo de la proyección $arepsilon _{3}$.

Luego lo normalizamos:

Procedemos así hasta obtener el último residuo normalizado $u_{K} $.

Al final del proceso, los vectores forman un conjunto ortonormal porque:

  1. son el resultado de una normalización, y como consecuencia tienen norma unitaria;

  2. cada $u_{k} se obtiene de un residuo que tiene la propiedad de ser ortogonal a .

Para completar esta visión general, recordemos que el span lineal de es el conjunto de todos los vectores que pueden escribirse como combinaciones lineales de ; se denota pory es un espacio lineal.

Dado que los vectores son combinaciones linealmente independientes de , cualquier vector que pueda escribirse como combinación lineal de también puede escribirse como combinación lineal de . Por lo tanto, los espacios de los dos conjuntos de vectores coinciden:

Enunciado formal

Formalizamos aquí el proceso de Gram-Schmidt como una proposición, cuya demostración contiene todos los detalles técnicos del procedimiento.

Proposición Sea $S$ un espacio vectorial dotado de un producto interior . Sean vectores linealmente independientes. Entonces, existe un conjunto de vectores ortonormales tal quepara cualquier $kleq K$.

Prueba

La prueba es por inducción: primero probamos que la proposición es cierta para $k=1$, y luego probamos que es cierta para un k genérico si se cumple para $k-1$. Cuando $k=1$, el vector tiene norma unitaria y constituye por sí mismo un conjunto ortonormal: no hay otros vectores, por lo que la condición de ortogonalidad se cumple trivialmente. El conjunto es el conjunto de todos los múltiplos escalares de $s_{1}$, que también son múltiplos escalares de $u_{1}$ (y viceversa). Por tanto, Ahora, supongamos que la proposición es cierta para $k-1$. Entonces, podemos proyectar $s_{k}$ sobre :donde el residuo $arepsilon _{k}$ es ortogonal a . Supongamos que $arepsilon _{k}=0$. Entonces,Dado que, por suposición, para cualquier $jleq k$, tenemos que para cualquier $jleq k-1$, donde $lpha _{jl}$ son escalares. Por tanto,En otras palabras, la suposición de que $arepsilon _{k}=0$ lleva a la conclusión de que $s_{k}$ es una combinación lineal de . Pero esto es imposible porque uno de los supuestos de la proposición es que son linealmente independientes. En consecuencia, debe ser que . Por tanto, podemos normalizar el residuo y definir el vector que tiene norma unitaria. Ya sabemos que $arepsilon _{k}$ es ortogonal a . Esto implica que también $u_{k}$ es ortogonal a . Por tanto, es un conjunto ortonormal. Ahora, tomemos cualquier vector $sin S$ que pueda escribirse comodonde son escalares. Como, por suposición, tenemos que la ecuación (2) también se puede escribir como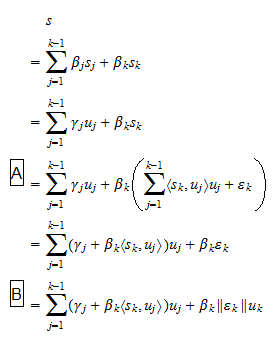donde son escalares, y: en el paso $marco{A}$ hemos utilizado la ecuación (1); en el paso $marco{B}$ hemos utilizado la definición de $u_{k}$. Así, hemos demostrado que todo vector que puede escribirse como una combinación lineal de también puede escribirse como una combinación lineal de . La suposición (3) permite demostrar lo contrario de forma completamente análoga: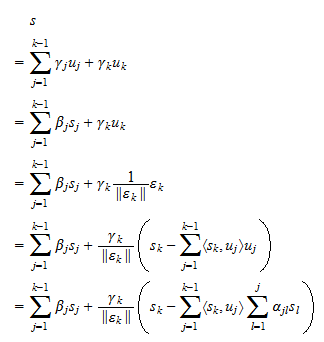 En otras palabras, toda combinación lineal de es también una combinación lineal de . Esto demuestra que y concluye la prueba.

Todo espacio de producto interno tiene una base ortonormal

La siguiente proposición presenta una importante consecuencia del proceso de Gram-Schmidt.

Proposición Sea $S$ un espacio vectorial dotado de un producto interno . Si $S$ tiene dimensión finita , entonces existe una base ortonormal para $S$.

Prueba

Como $S$ es de dimensión finita, existe al menos una base para $S$, formada por K vectores . Podemos aplicar el procedimiento de Gram-Schmidt a la base y obtener un conjunto ortonormal . Como es una base, abarca $S$. Por tanto, 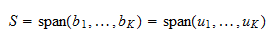Así pues, es una base ortonormal de $S$.

Ejercicios resueltos

A continuación puedes encontrar algunos ejercicios con soluciones explicadas.

Ejercicio 1

Consideremos el espacio $S$ de todos los vectores $3imes 1$ que tienen entradas reales y el producto interiordonde $r,sin S$ y $s^{op }$ es la transposición de $s$. Definir el vector

Normalizar $s$.

Solución

La norma de $s$ esPor tanto, la normalización de $s$ es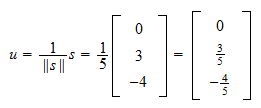

Ejercicio 2

Consideremos el espacio $S$ de todos los vectores $2imes 1$ que tienen entradas reales y el producto interiordonde $r,sin S$ . Consideremos los dos vectores linealmente independientes

Transfórmalos en un conjunto ortonormal mediante el proceso de Gram-Schmidt.

Solución

La norma de $s_{1}$ es Por tanto, el primer vector ortonormal esEl producto interior de $s_{2}$ y $u_{1}$ es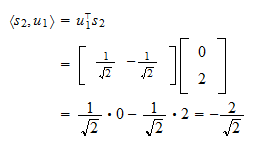La proyección de $s_{2}$ sobre $u_{1}$ es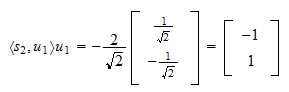El residuo de la proyección es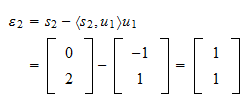La norma del residuo esy el residuo normalizado esAsí pues, el conjunto ortonormal que buscamos es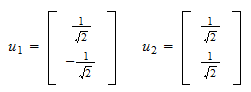

Cómo citar

Por favor, cite como:

Taboga, Marco (2017). «Proceso de Gram-Schmidt», Conferencias sobre álgebra matricial. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.

Leave a Reply