Parte 14 : Producto de puntos y de Hadamard
Además de la multiplicación de matrices comentada anteriormente, los vectores pueden multiplicarse por dos métodos más : Producto de puntos y Producto de Hadamard. Los resultados obtenidos por ambos métodos son diferentes.
Los elementos correspondientes a la misma fila y columna se multiplican juntos y los productos se suman de manera que, el resultado es un escalar.
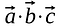
A diferencia de la multiplicación de matrices el resultado del producto punto no es otro vector o matriz, es un escalar.
El orden de los vectores no importa para el producto punto, sólo el número de elementos de ambos vectores debe ser igual.
La fórmula geométrica del producto punto es
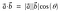
El producto punto también se llama producto interior o producto escalar.
Proyección de vectores
Suponiendo que tenemos dos vectores c y d, subtendidos por el ángulo, phi(Ф).
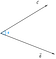
Ahora, la proyección del vector c sobre el vector d podría representarse como
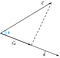
Podemos concluir de la figura que la proyección es igual a la componente horizontal del vector c con respecto al ángulo phi(Ф).
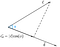
Esto se llama proyección escalar.Para encontrar la proyección vectorial del vector c sobre el vector d tenemos que multiplicar la proyección escalar por el vector unitario d.
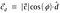
Sustituyendo el valor del vector unitario d.
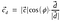
Así, el producto punto también podría representarse como
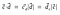
Las proyecciones tienen un amplio uso en el álgebra lineal y el aprendizaje automático (Support Vector Machine(SVM) es un algoritmo de aprendizaje automático, utilizado para la clasificación de datos).
Producto de Hadamard (Multiplicación por elementos)
El producto de Hadamard de dos vectores es muy similar a la suma de matrices, los elementos correspondientes a la misma fila y columnas de vectores/matrices dados se multiplican juntos para formar un nuevo vector/matriz.
Se llama así por el matemático francés Jacques Hadamard.
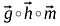
El orden de las matrices/vectores a multiplicar debe ser el mismo y la matriz resultante también será del mismo orden.
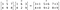

El producto de Hadamard se utiliza en técnicas de compresión de imágenes como JPEG. También se conoce como producto de Schur en honor al matemático alemán Issai Schur.
El producto de Hadamard se utiliza en las celdas LSTM (Long Short-Term Memory) de las redes neuronales recurrentes (RNN).
Leave a Reply