Muestreo de Gibbs
Otro método MCMC
Como otros métodos MCMC, el muestreador de Gibbs construye una cadena de Markov cuyos valores convergen hacia una distribución objetivo. El muestreo de Gibbs es, de hecho, un caso específico del algoritmo de Metrópolis-Hastings en el que las propuestas son siempre aceptadas.
Para elaborar, suponga que quiere muestrear una distribución de probabilidad multivariable.

Nota: Una distribución de probabilidad multivariante es una función de múltiples variables (es decir distribución normal de 2 dimensiones).

No sabemos cómo muestrear de esta última directamente. Sin embargo, por alguna conveniencia matemática o tal vez por pura suerte, resulta que conocemos las probabilidades condicionales.

Aquí es donde entra el muestreo de Gibbs. El muestreo de Gibbs es aplicable cuando la distribución conjunta no se conoce explícitamente o es difícil de muestrear directamente, pero la distribución condicional de cada variable se conoce y es más fácil de muestrear.
Empezamos seleccionando un valor inicial para las variables aleatorias X & Y. A continuación, muestreamos de la distribución de probabilidad condicional de X dada Y = Y⁰ denotada p(X|Y⁰). En el siguiente paso, muestreamos un nuevo valor de Y condicionado a X¹, que acabamos de calcular. Repetimos el procedimiento durante n – 1 iteraciones adicionales, alternando entre la extracción de una nueva muestra de la distribución de probabilidad condicional de X y la distribución de probabilidad condicional de Y, dado el valor actual de la otra variable aleatoria.

Veamos un ejemplo. Supongamos que tenemos las siguientes distribuciones de probabilidad posterior y condicional.


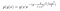
donde g(y) contiene los términos que no incluyen a x, y g(x) contiene los que no dependen de y.
No conocemos el valor de C (constante normalizadora). Sin embargo, sí conocemos las distribuciones de probabilidad condicional. Por lo tanto, podemos utilizar el Muestreo de Gibbs para aproximar la distribución posterior.
Nota: Las probabilidades condicionales son en realidad distribuciones normales, y se pueden reescribir de la siguiente manera.

Dadas las ecuaciones anteriores, procedemos a implementar el algoritmo de Muestreo de Gibbs en Python. Para empezar, importamos las siguientes librerías.
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()
Definimos la función para la distribución posterior (asumimos C=1).
f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)
A continuación, trazamos la distribución de probabilidad.
xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Ahora, intentaremos estimar la distribución de probabilidad utilizando el muestreo de Gibbs. Como hemos mencionado anteriormente, las probabilidades condicionales son distribuciones normales. Por lo tanto, podemos expresarlas en términos de mu y sigma.
En el siguiente bloque de código, definimos funciones para mu y sigma, inicializamos nuestras variables aleatorias X & Y, y establecemos N (el número de iteraciones).
N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)
Pasamos por el algoritmo de muestreo de Gibbs.
for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x
Por último, trazamos los resultados.
plt.hist(x, bins=50);
plt.hist(y, bins=50);


plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

Como podemos ver, la distribución de probabilidad obtenida mediante el algoritmo de muestreo de Gibbs hace un buen trabajo de aproximación a la distribución objetivo.
Conclusión
El Muestreo de Gibbs es un método de Cadena de Markov de Monte Carlo que dibuja iterativamente una instancia de la distribución de cada variable, condicionada a los valores actuales de las otras variables para estimar distribuciones conjuntas complejas. A diferencia del algoritmo Metrópolis-Hastings, siempre se acepta la propuesta. Así, el muestreo de Gibbs puede ser mucho más eficiente.
Leave a Reply