Matemáticas para las artes liberales
Resultados del aprendizaje
- Define e identifica la autosimilitud en formas geométricas, plantas, y formaciones geológicas
- Generar una forma fractal dado un iniciador y un generador
- Escalar un objeto geométrico por un factor de escala específico utilizando la relación de dimensión de escala
- Determinar la dimensión fractal de un objeto fractal
Además de la autosimilitud visual, los fractales muestran otras propiedades interesantes. Por ejemplo, observe que cada paso de la iteración de la junta de Sierpinski elimina una cuarta parte del área restante. Si este proceso se continúa indefinidamente, terminaríamos esencialmente eliminando toda el área, lo que significa que empezamos con un área de 2 dimensiones, y de alguna manera terminamos con algo menos que eso, pero aparentemente más que una simple línea de 1 dimensión.
Para explorar esta idea, necesitamos discutir la dimensión. Algo como una línea es unidimensional; sólo tiene longitud. Cualquier curva es unidimensional. Objetos como las cajas y los círculos son bidimensionales, ya que tienen longitud y anchura, describiendo un área. Los objetos como las cajas y los cilindros tienen longitud, anchura y altura, describiendo un volumen, y son tridimensionales.
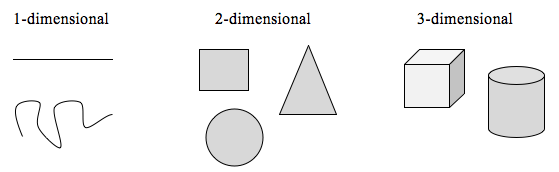
Se aplican ciertas reglas para escalar objetos, relacionadas con su dimensión.
Si tuviera una línea de longitud 1, y quisiera escalar su longitud en 2, necesitaría dos copias de la línea original. Si tuviera una línea de longitud 1, y quisiera escalar su longitud en 3, necesitaría tres copias de la original.
Si tuviera un rectángulo con longitud 2 y altura 1, y quisiera escalar su longitud y anchura en 2, necesitaría cuatro copias del rectángulo original. Si quisiera escalar la longitud y la anchura en 3, necesitaría nueve copias del rectángulo original.
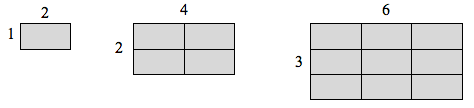
Si tuviera una caja cúbica con lados de longitud 1, y quisiera escalar su longitud y anchura en 2, necesitaría ocho copias del cubo original. Si quisiera escalar la longitud y la anchura en 3, necesitaría 27 copias del cubo original.
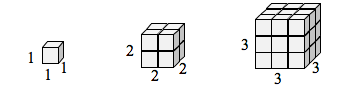
Nota que en el caso de 1 dimensión, copias necesarias = escala.
En el caso de 2 dimensiones, copias necesarias = escala^{2}.
En el caso de 3 dimensiones, copias necesarias = escala^{3}.
De estos ejemplos, podríamos inferir un patrón.
Relación escala-dimensión
Para escalar una forma de dimensión D por un factor de escala S, el número de copias C de la forma original necesarias vendrá dado por:
{copias}={escala}^{dimensión}}, o C=S^{D}
Ejemplo
Utilizar la relación escala-dimensión para determinar la dimensión de la junta de Sierpinski.
Supongamos que definimos que la junta original tiene una longitud de lado 1. La junta más grande que se muestra tiene el doble de ancho y el doble de alto, por lo que se ha escalado por un factor de 2.
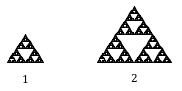
Nota que para construir la junta más grande, se necesitan 3 copias de la junta original.
Usando la relación escala-dimensión C=S^{D}, obtenemos la ecuación 3=2^{D}.
Dado que 2^{1}=2 y 2^{2}=4, podemos ver inmediatamente que D está en algún lugar entre 1 y 2; la junta es más que una forma de 1 dimensión, pero hemos quitado tanta área que ahora es menos de 2 dimensiones.
Resolver la ecuación 3=2^{D} requiere logaritmos. Si has estudiado antes los logaritmos, puede que recuerdes cómo resolver esta ecuación (si no es así, salta al recuadro de abajo y utiliza esa fórmula con la tecla logarítmica de una calculadora):
Toma el logaritmo de ambos lados.
3={2}^{D}
Usa la propiedad del exponente de los logaritmos.
\log(3)=\log({{2}^{D}}\️)
Divide por log(2).
\log(3)=D\log(2\\a la derecha)
La dimensión de la junta es aproximadamente 1,585.
D=\frac{log\a la izquierda(3\a la derecha)}{\log(2)}aproximadamentex1.585
Relación Escala-Dimensión, para hallar la Dimensión
Para hallar la dimensión D de un fractal, determine el factor de escala S y el número de copias C de la forma original necesarias, a continuación, utilice la fórmula
D=\frac{\log\left(C\right)}{\log(S)}
Inténtelo
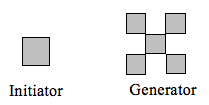
Determine la dimensión fractal del fractal producido utilizando el iniciador y el generador.
En el siguiente vídeo, presentamos un ejemplo trabajado de cómo determinar la dimensión del empaque de Sierpinski

Leave a Reply