Introducción al Hashing Consistente

30 de abril, 2020 – 11 min read

Con el auge de las arquitecturas distribuidas, el hashing consistente se ha convertido en la corriente principal. Pero, ¿qué es exactamente y en qué se diferencia de un algoritmo hash estándar? ¿Cuáles son las motivaciones exactas detrás de él?

Primero, describiremos los conceptos principales. A continuación, profundizaremos en los algoritmos existentes para entender los retos asociados al hashing consistente.

Hashing

El hashing es el proceso de asignar datos de tamaño arbitrario a valores de tamaño fijo. Cada algoritmo existente tiene su propia especificación:

• MD5 produce valores hash de 128 bits.
• SHA-1 produce valores hash de 160 bits.
• etc.

Hashing tiene muchas aplicaciones en informática. Por ejemplo, una de estas aplicaciones se llama suma de comprobación. Para verificar la integridad de un conjunto de datos es posible utilizar un algoritmo de hash. Un servidor realiza el hash de un conjunto de datos e indica el valor del hash a un cliente. A continuación, el cliente realiza el hash de su versión del conjunto de datos y compara los valores hash. Si son iguales, la integridad debería ser verificada.

El «debería» aquí es importante. El peor escenario es cuando se produce una colisión. Una colisión es cuando dos piezas distintas de datos tienen el mismo valor hash. Tomemos un ejemplo de la vida real definiendo la siguiente función hash: dada una persona, devuelve la fecha de su cumpleaños (día & mes de nacimiento). La paradoja del cumpleaños nos dice que si sólo hay 23 personas en una sala, la probabilidad de que dos personas tengan el mismo cumpleaños (y por tanto una colisión) es superior al 50%. Por lo tanto, la función de cumpleaños probablemente no es una buena función de hashing.

Como introducción rápida al hashing es importante entender que la idea principal es repartir valores en un dominio. Por ejemplo:

• MD5 distribuye valores a través de un dominio de espacio de 128 bits
• Una tabla hash (o hashmap) respaldada por un array de 32 elementos tiene una función hash interna que distribuye valores a cualquier índice (de 0 a 31).

Distribución de la carga

La distribución de la carga puede definirse como el proceso de distribución de la carga a través de los nodos. El término nodo aquí es intercambiable con servidor o instancia. Es una unidad de computación.

El equilibrio de carga es un ejemplo de distribución de carga. Se trata de distribuir un conjunto de tareas sobre un conjunto de recursos. Por ejemplo, usamos el balanceo de carga para distribuir las peticiones de la API entre las instancias del servidor web.

Cuando se trata de datos, usamos más bien el término sharding. Un shard de base de datos es una partición horizontal de datos en una base de datos. Un ejemplo típico es una base de datos dividida en tres fragmentos donde cada fragmento tiene un subconjunto de los datos totales.

El equilibrio de carga y la fragmentación comparten algunos desafíos comunes. Repartir los datos uniformemente, por ejemplo, para garantizar que un nodo no esté sobrecargado en comparación con los demás. En algún contexto, el balanceo de carga y el sharding también necesitan seguir asociando tareas o datos al mismo nodo:

• Si necesitamos serializar, manejar una a una, las operaciones para un determinado consumidor, debemos enrutar la petición al mismo nodo.
• Si necesitamos distribuir datos, debemos saber qué shard es el propietario para una clave concreta.

¿Te suena familiar? En estos dos ejemplos, repartimos valores en un dominio. Ya sea una tarea repartida en los nodos del servidor o los datos repartidos en el fragmento de la base de datos, volvemos a encontrar la idea asociada al hashing. Esta es la razón por la que el hashing se puede utilizar junto con la distribución de la carga. Veamos cómo.

Mod-n Hashing

El principio de mod-n hashing es el siguiente. Cada clave se convierte en hash utilizando una función hash para transformar una entrada en un número entero. Luego, realizamos un módulo basado en el número de nodos.

Veamos un ejemplo concreto con 3 nodos. Aquí, necesitamos distribuir la carga entre estos nodos en base a un identificador de clave. Cada clave es hash y luego realizamos una operación de módulo:

La ventaja de este enfoque es su ausencia de estado. No tenemos que mantener ningún estado que nos recuerde que foo fue enrutado al nodo 2. Sin embargo, necesitamos saber cuántos nodos están configurados para aplicar la operación de módulo.

Entonces, ¿cómo funciona el mecanismo en caso de escalar hacia fuera o hacia dentro (añadiendo o quitando nodos)? Si añadimos otro nodo, la operación de módulo se basa ahora en 4 en lugar de 3:

Como podemos ver, las claves foo y baz ya no están asociadas al mismo nodo. Con el hashing mod-n, no hay garantía de mantener ninguna consistencia en la asociación clave/nodo. ¿Es esto un problema? Puede ser.

¿Qué pasa si implementamos un datastore usando sharding y basado en la estrategia mod-n para distribuir los datos? Si escalamos el número de nodos, necesitamos realizar una operación de rebalanceo. En el ejemplo anterior, rebalancear significa:

• Mover foo del nodo 2 al nodo 0.
• Mover baz del nodo 2 al nodo 3.

Ahora, ¿qué pasa si tuviéramos almacenados millones o incluso miles de millones de datos y que necesitáramos rebalancear casi todo? Como podemos imaginar, esto sería un proceso pesado. Por lo tanto, debemos cambiar nuestra técnica de distribución de la carga para asegurarnos de que al reequilibrar:

• La distribución siga siendo lo más uniforme posible en función del nuevo número de nodos.
• El número de claves que tenemos que migrar debe ser limitado. Idealmente, sería sólo 1/n por ciento de las claves donde n es el número de nodos.

Este es exactamente el propósito de los algoritmos hashing consistentes.

El término consistente podría ser algo confuso sin embargo. Conocí a ingenieros que daban por sentado que tales algoritmos seguían asociando una clave determinada al mismo nodo incluso ante la escalabilidad. Este no es el caso. Tiene que ser consistente hasta cierto punto para mantener la distribución uniforme.

Ahora, es el momento de profundizar en algunas soluciones.

Rendezvous

Rendezvous fue el primer algoritmo propuesto para resolver nuestro problema. Aunque el estudio original, publicado en 1996, no menciona el término hashing consistente, proporciona una solución a los retos que hemos descrito. Veamos una posible implementación en Go:

¿Cómo funciona? Recorremos cada nodo y calculamos su valor hash. El valor hash es devuelto por una función hash que produce un entero basado en una clave (nuestra entrada) y un identificador de nodo (el enfoque más fácil es hacer un hash de la concatenación de las dos cadenas). A continuación, devolvemos el nodo con el valor hash más alto. Esta es la razón por la que el algoritmo también se conoce como hashing de peso aleatorio más alto.

El principal inconveniente de rendezvous es su complejidad de tiempo O(n) donde n es el número de nodos. Es muy eficiente si necesitamos tener un número limitado de nodos. Sin embargo, si empezamos a mantener miles de nodos, podría empezar a causar problemas de rendimiento.

Ring Consistent Hash

El siguiente algoritmo fue publicado en 1997 por Karger et al. en este documento. En este estudio se menciona por primera vez el término hashing consistente.

Se basa en un anillo (una matriz conectada de extremo a extremo). Aunque es el algoritmo de hashing consistente más popular (o al menos el más conocido), el principio no siempre se entiende bien. Vamos a sumergirnos en él.

La primera operación es crear el anillo. Un anillo tiene una longitud fija. En nuestro ejemplo, lo dividimos en 12 partes:

A continuación, colocamos nuestros nodos. En nuestro ejemplo definiremos N0, N1 y N2.

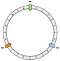
Los nodos se distribuyen uniformemente por el momento. Volveremos a este punto más adelante.

Entonces, es el momento de ver cómo representar las claves. Primero, necesitamos una función f que devuelva un índice de anillo (de 0 a 11) basado en una clave. Para ello podemos utilizar el hashing mod-n. Como la longitud del anillo es constante, no nos causará ningún problema.

En nuestro ejemplo definiremos 3 claves: a, b y c. Aplicamos f en cada una de ellas. Supongamos que tenemos los siguientes resultados:

• f(a) = 1
• f(a) = 5
• f(a) = 7

Por lo tanto, podemos colocar las llaves en el anillo de esta manera:

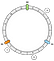
¿Cómo asociamos una llave determinada a un nodo? La lógica principal es avanzar. A partir de una clave dada, devolvemos el primer nodo que encontremos a continuación mientras avanzamos:

En este ejemplo, asociamos a a N1, b y c a N2.

Ahora, veamos cómo se gestiona el rebalanceo. Definimos otro nodo N3. ¿Dónde debemos colocarlo? Ya no hay espacio para que la distribución global sea uniforme. ¿Debemos reorganizar los nodos? No, de lo contrario ya no seríamos coherentes, ¿no es así? Para posicionar un nodo, reutilizamos la misma función hashing f que introdujimos. En lugar de ser llamada con una clave, puede ser llamada con un identificador de nodo. Así la posición del nuevo nodo se decide al azar.

Surge entonces una pregunta: ¿qué debemos hacer con a ya que el siguiente nodo ya no es N1:

La solución es la siguiente: debemos cambiar su asociación y conseguir que a se asocie a N3:

Como hemos comentado anteriormente, un algoritmo ideal debería reequilibrar 1/n por ciento de las claves de media. En nuestro ejemplo, como estamos añadiendo un cuarto nodo, deberíamos tener el 25% de las posibles claves reasociadas a N3. ¿Es éste el caso?

• N0 de los índices 8 a 12: 33,3% del total de claves
• N1 de los índices 2 a 4: 16,6% del total de claves
• N2 de los índices 4 a 8: 33.3% del total de claves
• N3 de los índices 0 a 2: 16,6% del total de claves

La distribución no es uniforme. ¿Cómo podemos mejorarla? La solución es utilizar nodos virtuales.

Digamos que en lugar de posicionar un solo punto por nodo, podemos posicionar tres. Además, tenemos que definir tres funciones hash diferentes. Cada nodo tiene tres hashes, de modo que obtenemos tres índices diferentes:

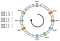
Podemos aplicar el mismo algoritmo avanzando. Sin embargo, una clave se asociaría a un nodo independientemente del nodo virtual con el que se encontrara.

En este mismo ejemplo, la distribución sería ahora la siguiente:

• N0: 33,3%
• N1: 25%
• N2: 41,6%

Cuanto más nodo virtual definamos por nodo, más uniforme debería ser la distribución. Por término medio, con 100 nodos virtuales por servidor, la distribución estándar es de aproximadamente el 10%. Con 1000, es de un 3,2%.

Este mecanismo también es útil si tenemos nodos con diferente tamaño. Por ejemplo, si un nodo está configurado para manejar teóricamente el doble de carga que los demás, podríamos hacer girar el doble de nodos virtuales.

Sin embargo, el principal inconveniente con los nodos virtuales es la huella de memoria. Si tenemos que manejar miles de servidores, se necesitarían megabytes de memoria.

Antes de continuar, es interesante observar que a veces un algoritmo puede mejorarse sustancialmente cambiando una pequeña parte. Es el caso, por ejemplo, de un algoritmo publicado por Google en 2017 llamado consistent hashing with bounded loads. Esta versión se basa en la misma idea del anillo que hemos descrito. Sin embargo, su enfoque consiste en realizar un pequeño reequilibrio ante cualquier actualización (una nueva clave o un nodo añadido/eliminado). Esta versión supera a la original en términos de desviación estándar con la contrapartida de una peor complejidad temporal.

Jump Consistent Hash

En 2007, dos ingenieros de Google publicaron jump consistent hash. En comparación con el algoritmo basado en anillos, esta implementación «no requiere almacenamiento, es más rápida y hace un mejor trabajo de dividir uniformemente el espacio de claves entre los cubos y de dividir uniformemente la carga de trabajo cuando el número de cubos cambia». Dicho de otro modo, mejora la distribución de la carga de trabajo entre los nodos (un cubo es el mismo concepto que un nodo) sin ninguna sobrecarga de memoria.

Aquí está el algoritmo en C++ (7 líneas de código 🤯):

En el hash consistente en anillo, con 1000 nodos virtuales la desviación estándar era de alrededor del 3,2%. En el hash consistente en saltos, ya no necesitamos el concepto de nodos virtuales. Sin embargo, la desviación estándar sigue siendo inferior al 0,0000001%.

Pero hay una limitación. Los nodos deben estar numerados secuencialmente. Si tenemos una lista de servidores foo, bar y baz, no podemos eliminar bar por ejemplo. Sin embargo, si configuramos un almacén de datos, podemos aplicar el algoritmo para obtener el índice de shards basado en el número total de shards. Por lo tanto, el hash consistente de salto puede ser útil en el contexto de sharding pero no de balanceo de carga.

¿Qué es el Algoritmo de Hashing Consistente Perfecto?

Como ya tenemos algo de experiencia con el hashing consistente, demos un paso atrás y veamos cuál sería el algoritmo perfecto:

• Sólo 1/n por ciento de las claves serían reasignadas en promedio donde n es el número de nodos.
• Una complejidad espacial O(n) donde n es el número de nodos.
• Una complejidad de tiempo O(1) por inserción/eliminación de un nodo y por búsqueda de claves.
• Una desviación estándar mínima para asegurarse de que un nodo no está sobrecargado en comparación con otro.
• Permitiría asociar un peso a un nodo para hacer frente a diferentes tamaños de nodos.
• Permitiría nombrar nodos arbitrariamente (no numerados secuencialmente) para soportar tanto el equilibrio de carga como la fragmentación.

Desgraciadamente, este algoritmo no existe. Basado en lo que vimos:

• Rendezvous tiene una complejidad de tiempo lineal por búsqueda.
• El hash consistente en anillos tiene una pobre desviación estándar mínima sin el concepto de nodos virtuales. Con nodos virtuales, su complejidad espacial es O(n*v) siendo n el número de nodos y v el número de nodos virtuales por nodo.
• El hash consistente de salto no tiene una complejidad de tiempo constante y no admite nombres de nodos arbitrarios.

El tema sigue abierto y hay estudios recientes que merecen la pena. Por ejemplo, el hash consistente multi-sonda lanzado en 2005. Soporta una complejidad espacial O(1). Sin embargo, para lograr una desviación estándar de ε, requiere O(1/ε) de tiempo por búsqueda. Por ejemplo, si queremos conseguir una desviación estándar inferior al 0,5%, se requiere hacer un hash de la clave unas 20 veces. Por lo tanto, podemos obtener una desviación estándar mínima pero con el esfuerzo de una mayor complejidad de tiempo de búsqueda.

Como dijimos en la introducción, los algoritmos de hashing consistente se convirtieron en la corriente principal. Ahora se utiliza en innumerables sistemas como MongoDB, Cassandra, Riak, Akka, etc. ya sea en el contexto de equilibrar la carga o distribuir los datos. Sin embargo, como a menudo en la ciencia de la computación, cada solución tiene ventajas y desventajas.

Hablando de ventajas y desventajas, si usted necesita un seguimiento, es posible que desee echar un vistazo a la excelente entrada escrita por Damian Gryski: