Introducción a la desconvolución

La desconvolución es una técnica de procesamiento de imágenes intensiva en términos computacionales que se utiliza cada vez más para mejorar el contraste y la resolución de las imágenes digitales capturadas en el microscopio. Los fundamentos se basan en un conjunto de métodos diseñados para eliminar o invertir el desenfoque presente en las imágenes del microscopio inducido por la apertura limitada del objetivo.

Casi cualquier imagen adquirida en un microscopio de fluorescencia digital puede ser deconvertida, y se están desarrollando varias aplicaciones nuevas que aplican técnicas de deconvolución a imágenes de luz transmitida recogidas bajo una variedad de estrategias de mejora del contraste. Entre los temas más adecuados para la mejora por deconvolución se encuentran los montajes tridimensionales construidos a partir de una serie de secciones ópticas.

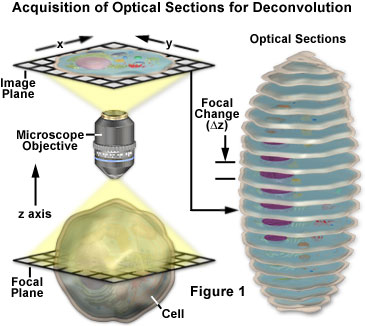
Los conceptos básicos que rodean la adquisición de imágenes de serie z para el análisis por deconvolución se presentan con un diagrama esquemático en la Figura 1. Se graba una serie de imágenes de la muestra, cada una de ellas desplazada ligeramente una de otra a lo largo del eje z. Este cambio en el plano focal da lugar a una imagen ligeramente diferente, con cambios sutiles causados por la luz desenfocada procedente de arriba y abajo del plano z actual. Durante el análisis de deconvolución, se analiza toda la serie z para crear un conjunto de datos más claro y de mayor resolución que no está convulsionado por la fluorescencia desenfocada.

La deconvolución se sugiere a menudo como una buena alternativa al microscopio confocal, ya que ambas técnicas buscan minimizar el efecto de la fluorescencia desenfocada en su imagen final. Esto no es estrictamente cierto, ya que las imágenes adquiridas mediante una apertura estenopeica en un microscopio confocal se benefician del procesamiento de la deconvolución. La microscopía confocal evita que se detecte la luz desenfocada colocando una abertura estenopeica entre el objetivo y el detector, a través de la cual sólo pueden pasar los rayos de luz enfocados. En cambio, los microscopios de campo amplio permiten que la luz desenfocada pase directamente al detector. La deconvolución se aplica entonces a las imágenes resultantes para sustraer la luz desenfocada o reasignarla a su fuente. La microscopía confocal es especialmente adecuada para examinar especímenes gruesos, como embriones o tejidos, mientras que el procesamiento de deconvolución de campo amplio ha demostrado ser una potente herramienta para obtener imágenes de especímenes que requieren niveles de luz extremadamente bajos. Estas herramientas pueden incluso combinarse para reducir el ruido en las imágenes adquiridas en un microscopio confocal. Sin embargo, la mayoría de los experimentos de deconvolución descritos en la literatura se aplican a imágenes grabadas en un microscopio de fluorescencia de campo amplio estándar.

Fuentes de degradación de la imagen

La degradación de la imagen puede dividirse en cuatro fuentes independientes: ruido, dispersión, deslumbramiento y desenfoque. La figura 2 presenta ejemplos del impacto visual de cada una de ellas en la misma imagen.

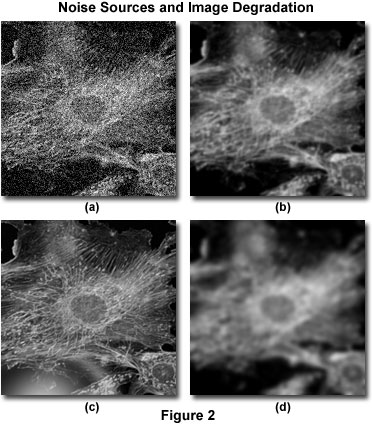
El ruido puede describirse como una desorganización casi aleatoria de los detalles en una imagen, que (en su forma más grave) tiene la apariencia de ruido blanco o ruido de sal y pimienta, similar a lo que se ve en la televisión cuando se experimenta una mala recepción (figura 2(a)). Este tipo de ruido se denomina «cuasi-aleatorio» porque la distribución estadística puede predecirse si se conoce la mecánica de la fuente. En la microscopía digital, la principal fuente de ruido es la propia señal (a menudo denominada ruido de disparo de fotones) o el sistema de imagen digital. Se conoce la mecánica de ambas fuentes de ruido y, por tanto, la distribución estadística del ruido. El ruido dependiente de la señal puede caracterizarse por una distribución de Poisson, mientras que el ruido procedente del sistema de imagen suele seguir una distribución gaussiana. Dado que el origen y la distribución del ruido común en las imágenes digitales se conoce tan bien, puede eliminarse fácilmente mediante la aplicación de los filtros de imagen adecuados, que suelen incluirse en la mayoría de los paquetes de software de deconvolución como una rutina opcional de «preprocesamiento».

La dispersión suele denominarse una perturbación aleatoria de la luz inducida por los cambios en el índice de refracción de una muestra. El efecto neto de la dispersión es un desorden verdaderamente aleatorio de los detalles de la imagen, como se manifiesta en la figura 2(b). Aunque no se ha desarrollado ningún método completamente satisfactorio para predecir la dispersión en una muestra determinada, se ha demostrado que el grado de dispersión depende en gran medida del grosor de la muestra y de las propiedades ópticas de la muestra y de los materiales circundantes. La dispersión aumenta tanto con el grosor de la muestra como con la heterogeneidad del índice de refracción que presentan los componentes internos de una muestra.

Al igual que la dispersión, el resplandor es una perturbación aleatoria de la luz, pero se produce en los elementos ópticos (lentes, filtros, prismas, etc.) del microscopio y no dentro de la muestra. El nivel de deslumbramiento en un microscopio moderno se ha minimizado gracias al empleo de lentes y filtros con revestimientos antirreflectantes y al perfeccionamiento de las técnicas de conformación de las lentes, los cementos ópticos y las formulaciones del vidrio. La figura 2(c) ilustra el efecto del deslumbramiento incontrolado.

El desenfoque se describe como una dispersión no aleatoria de la luz que se produce al pasar por la trayectoria óptica del sistema de imagen (figura 2(d)). La fuente más significativa de desenfoque es la difracción, y una imagen cuya resolución está limitada únicamente por el desenfoque se considera limitada por la difracción. Esto representa un límite intrínseco de cualquier sistema de imagen y es el factor determinante para evaluar el límite de resolución de un sistema óptico. Afortunadamente, existen modelos sofisticados de desenfoque en un microscopio óptico que pueden utilizarse para determinar el origen de los fotones desenfocados. Esta es la base de la deconvolución. Debido a su importancia fundamental en la deconvolución, el modelo teórico del desenfoque se tratará con mucho más detalle en otras partes de esta sección. Sin embargo, hay que destacar que todos los sistemas de imagen producen desenfoque independientemente de las otras formas de degradación de la imagen inducidas por el espécimen o la electrónica instrumental que lo acompaña. Es precisamente esta independencia del desenfoque óptico de otros tipos de degradación lo que permite la posibilidad de eliminar el desenfoque mediante técnicas de deconvolución.

La interacción de la luz con la materia es el principal origen físico de la dispersión, el deslumbramiento y el desenfoque. Sin embargo, la composición y la disposición de las moléculas en un material determinado (ya sea vidrio, agua o proteínas) confiere a cada material su propio conjunto de propiedades ópticas. A efectos de la deconvolución, lo que distingue la dispersión, el resplandor y el desenfoque es el lugar donde se producen y la posibilidad de generar un modelo matemático para estos fenómenos. Dado que la dispersión es un fenómeno localizado e irregular que se produce en la muestra, ha resultado difícil de modelar. En cambio, como el desenfoque es una función del sistema óptico del microscopio (principalmente el objetivo), puede modelarse con relativa sencillez. Este modelo permite invertir el proceso de desenfoque matemáticamente, y la deconvolución emplea este modelo para invertir o eliminar el desenfoque.

La función de dispersión de puntos

El modelo de desenfoque que ha evolucionado en la óptica teórica se basa en el concepto de una función de dispersión de puntos (PSF) tridimensional. Este concepto es de importancia fundamental para la deconvolución y debe entenderse claramente para evitar los artefactos de imagen. La función de dispersión de puntos se basa en una fuente de luz puntual infinitamente pequeña que se origina en el espacio de la muestra (objeto). Dado que el sistema de imágenes del microscopio sólo recoge una fracción de la luz emitida por este punto, no puede enfocar la luz en una imagen tridimensional perfecta del punto. En su lugar, el punto aparece ensanchado y extendido en un patrón de difracción tridimensional. Así, la función de dispersión de puntos se define formalmente como el patrón de difracción tridimensional generado por una fuente de luz puntual ideal.

Dependiendo del modo de obtención de imágenes que se utilice (campo amplio, confocal, luz transmitida), la función de dispersión de puntos tiene una forma y un contorno diferentes y únicos. En un microscopio de fluorescencia de campo amplio, la forma de la función de dispersión de puntos se asemeja a la de un «balón» oblongo de luz rodeado por una llamarada de anillos que se ensanchan. Para describir la función de dispersión puntual en tres dimensiones, es habitual aplicar un sistema de coordenadas de tres ejes (x, y y z) donde × e y son paralelos al plano focal de la muestra y z es paralelo al eje óptico del microscopio. En este caso, la función de dispersión puntual aparece como un conjunto de anillos concéntricos en el plano x-y, y se asemeja a un reloj de arena en los planos x-z e y-z (como se ilustra en la figura 3). Un corte x-y a través del centro de la función de dispersión puntual de campo amplio revela un conjunto de anillos concéntricos: el llamado disco de Airy al que se suele hacer referencia en los textos sobre microscopía óptica clásica.

En la figura 3 se presentan dos proyecciones x-z de funciones de dispersión puntual que muestran diferentes grados de aberración esférica. El eje óptico es paralelo al eje vertical de la imagen. La función de dispersión de puntos de la izquierda muestra una aberración esférica mínima, mientras que la de la derecha muestra un grado significativo de aberración. Obsérvese que la asimetría axial y el ensanchamiento del nodo central a lo largo del eje óptico en la imagen de la derecha conducen a la degradación de la resolución axial y al desenfoque de la señal. En teoría, el tamaño de la función de dispersión de puntos es infinito, y la intensidad total sumada de la luz en los planos alejados del foco es igual a la intensidad sumada en el foco. Sin embargo, la intensidad de la luz disminuye rápidamente y acaba siendo indistinguible del ruido. En una función de dispersión de puntos no aberrada registrada con un objetivo de inmersión en aceite de alta apertura numérica (1,40), la luz que ocupa 0,2 micrómetros cuadrados en el plano de enfoque se dispersa en 90 veces esa área a 1 micrómetro por encima y por debajo del enfoque. El espécimen utilizado para registrar estas imágenes de la función de dispersión de puntos era una perla fluorescente de 0,1 micrómetros de diámetro montada en glicerol (índice de refracción igual a 1,47), con aceites de inmersión con los índices de refracción indicados en la figura.

Una consideración importante es cómo la función de dispersión de puntos afecta a la formación de imágenes en el microscopio. El modelo teórico de formación de imágenes trata la función de dispersión de puntos como la unidad básica de una imagen. En otras palabras, la función de dispersión de puntos es a la imagen lo que el ladrillo es a la casa. Lo mejor que puede ser una imagen es un conjunto de funciones de dispersión de puntos, y aumentar el aumento no cambiará este hecho. Como explica un célebre libro de texto de óptica teórica (Born and Wolf: Principles of Optics), «es imposible sacar a la luz detalles que no están presentes en la imagen primaria aumentando la potencia del ocular, ya que cada elemento de la imagen primaria es un pequeño patrón de difracción, y la imagen real, tal y como la ve el ocular, es sólo el conjunto de las imágenes ampliadas de estos patrones».

Como ejemplo, consideremos una población de perlas fluorescentes de baja resolución intercaladas entre un cubreobjetos y una platina de microscopio. Una imagen enfocada de este espécimen revela una nube de puntos, que en realidad es un disco rodeado por un pequeño conjunto de anillos (en efecto, un disco de Airy; véase la figura 4(a)). Si este espécimen se desenfoca ligeramente, aparecerá un conjunto más grande de anillos concéntricos donde estaba cada punto en la imagen enfocada (Figura 4(b)). Cuando se recoge una imagen tridimensional de este espécimen, se registra una función de dispersión de puntos completa para cada cuenta. La función de dispersión de puntos describe lo que le ocurre a cada fuente de luz puntual después de que pase por el sistema de imágenes.

El proceso de desenfoque que acabamos de describir se modela matemáticamente como una convolución. La operación de convolución describe la aplicación de la función de dispersión de puntos a cada punto de la muestra: la luz emitida desde cada punto del objeto se convoluciona con la función de dispersión de puntos para producir la imagen final. Lamentablemente, esta convolución hace que los puntos de la muestra se conviertan en regiones borrosas en la imagen. El brillo de cada punto de la imagen está relacionado linealmente por la operación de convolución con la fluorescencia de cada punto de la muestra. Dado que la función de dispersión de puntos es tridimensional, el desenfoque de la función de dispersión de puntos es un fenómeno inherentemente tridimensional. La imagen de cualquier plano focal contiene la luz borrosa de los puntos situados en ese plano mezclada con la luz borrosa de los puntos originados en otros planos focales.

La situación puede resumirse con la idea de que la imagen está formada por una convolución de la muestra con la función de dispersión de puntos. La desconvolución invierte este proceso e intenta reconstruir el espécimen a partir de una imagen borrosa.

Aberraciones en la función de dispersión de puntos

La función de dispersión de puntos puede definirse teóricamente utilizando un modelo matemático de difracción o empíricamente adquiriendo una imagen tridimensional de una perla fluorescente (véase la figura 3). Una función de dispersión puntual teórica suele tener simetría axial y radial. En efecto, la función de dispersión puntual es simétrica por encima y por debajo del plano x-y (simetría axial) y en rotación alrededor del eje z (simetría radial). Una función de dispersión de puntos empírica puede desviarse significativamente de la simetría perfecta (como se presenta en la figura 3). Esta desviación, más comúnmente conocida como aberración, se produce por irregularidades o desajustes en cualquier componente del tren óptico del sistema de imagen, especialmente el objetivo, pero también puede ocurrir con otros componentes como espejos, divisores de haz, lentes de tubo, filtros, diafragmas y aperturas. Cuanto mayor sea la calidad de los componentes ópticos y mejor sea la alineación del microscopio, más se acercará la función de dispersión de puntos empírica a su forma simétrica ideal. Tanto la microscopía confocal como la de deconvolución dependen de que la función de dispersión de puntos se acerque lo más posible al caso ideal.

La aberración más común encontrada en la microscopía óptica, bien conocida por cualquier microscopista experimentado y profesional, es la aberración esférica. La manifestación de esta aberración es una asimetría axial en la forma de la función de dispersión de puntos, con el correspondiente aumento de tamaño, especialmente a lo largo del eje z (Figura 3). El resultado es una considerable pérdida de resolución y de intensidad de la señal. En la práctica, la fuente típica de aberración esférica es un desajuste entre los índices de refracción del medio de inmersión de la lente frontal del objetivo y el medio de montaje en el que se baña la muestra. Hay que insistir mucho en la importancia de minimizar esta aberración. Aunque la deconvolución puede restaurar parcialmente la resolución perdida, ninguna cantidad de procesamiento de imágenes puede restaurar la señal perdida.