Función de Green

En general, una función de Green es un núcleo integral que puede usarse para resolver ecuaciones diferenciales de un gran número de familias, incluyendo ejemplos más simples como las ecuaciones diferenciales ordinarias con condiciones de valor inicial o de frontera, así como ejemplos más difíciles como las ecuaciones diferenciales parciales (EDP) no homogéneas con condiciones de frontera. Importantes por varias razones, las funciones de Green permiten interpretar visualmente las acciones asociadas a una fuente de fuerza o a una carga concentrada en un punto (Qin 2014), lo que las hace especialmente útiles en áreas de la matemática aplicada. En particular, los métodos de las funciones de Green son ampliamente utilizados en, por ejemplo, la física y la ingeniería.

Más precisamente, dado un operador diferencial lineal que actúa sobre la colección de distribuciones sobre un subconjunto de algún espacio euclidiano , una función de Green en el punto correspondiente a es cualquier solución de

(1)

donde denota la función delta. La motivación para definir tal función está muy extendida, pero multiplicando la identidad anterior por una función e integrando con respecto a se obtiene

(2)

El lado derecho se reduce simplemente a debido a las propiedades de la función delta, y como es un operador lineal que actúa sólo sobre y no sobre , el lado izquierdo puede reescribirse como

(3)

Esta reducción es particularmente útil al resolver para en ecuaciones diferenciales de la forma

(4)

donde la aritmética anterior confirma que

(5)

y de donde se deduce que tiene la forma integral específica

(6)

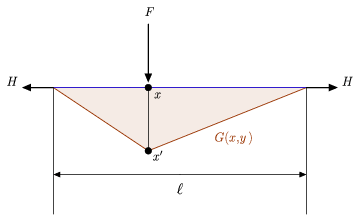
La figura anterior ilustra tanto la interpretación física intuitiva de una función de Green como una ecuación diferencial asociada relativamente sencilla con la que comparar la definición anterior (Hartmann 2013). En particular, muestra una cuerda tensa de longitud suspendida entre dos paredes, sujeta por una fuerza horizontal idéntica aplicada en cada uno de sus extremos, y una carga lateral colocada en algún punto interior de la cuerda. Sea el punto correspondiente a en la cuerda desviada, supongamos que la fuerza descendente es constante, digamos , y dejemos que denote la desviación de la cuerda. A este sistema físico le corresponde la ecuación diferencial

(7)

para con , un sistema cuya simplicidad permite escribir explícitamente tanto su solución como su función de Green :

(8)

y

(9)

respectivamente. Como se demuestra en la figura anterior, la cuerda desplazada tiene el formato lineal a trozos dado por anterior, confirmando así la afirmación de que la función de Green asociada a este sistema representa la acción de la cuerda horizontal correspondiente a la aplicación de una fuerza .

Una función de Green que toma un par de argumentos se denomina a veces función de Green de dos puntos. Esto contrasta con las funciones de Green multipunto que son de particular importancia en el área de la teoría de muchos cuerpos.

Como ejemplo elemental de una función de dos puntos como la definida anteriormente, considere el problema de determinar el potencial generado por una distribución de carga cuya densidad de carga es , por lo que las aplicaciones de la ecuación de Poisson y de la ley de Coulomb al potencial en producido por cada elemento de carga arrojan una solución

(10)

que se cumple, ¡bajo ciertas condiciones, en la región en la que . Como el lado derecho puede verse como un operador integral que convierte en , se puede reescribir esta solución en términos de una función de Green que tiene la forma

(11)

por lo que la solución puede reescribirse:

(12)

(Arfken 2012).

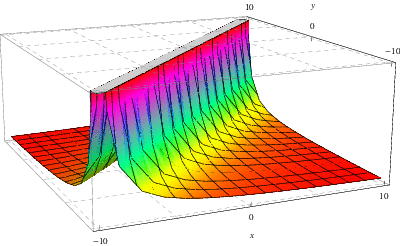
La figura anterior muestra la función de Green asociada a la solución de la ecuación – comentada anteriormente donde aquí, y , respectivamente , se representa en el eje -, respectivamente -.

Una lista algo exhaustiva de las funciones de Green correspondientes a varias ecuaciones diferenciales es mantenida en línea por Kevin Cole (Cole 2000).

Debido a la multitud de literatura escrita sobre las funciones de Green, pueden surgir varias notaciones y definiciones diferentes, algunas de las cuales son tópicamente diferentes de las anteriores pero que en general no afectan a las propiedades importantes de los resultados. Como ilustra el ejemplo anterior, por ejemplo, algunos autores prefieren denotar las variables y en términos de los vectores y para enfatizar el hecho de que son elementos de para algún que puede ser mayor que 1 (Arfken 1985). También es relativamente común ver la definición con signo negativo de manera que se define como la función para la cual

(13)

pero debido al hecho de que esta consideración puramente física no tiene ningún efecto sobre las matemáticas subyacentes, este punto de vista es generalmente pasado por alto. También se conocen otras notaciones para una función de Green, algunas de las cuales incluyen el uso de una minúscula en lugar de (Stakgold 1979), así como la inclusión de una línea vertical en lugar de una coma, por ejemplo (Duffy 2001).

En otros casos, la literatura presenta definiciones que están íntimamente relacionadas con los contextos en los que se presentan. Por ejemplo, algunos autores definen las funciones de Green como funciones que satisfacen un cierto conjunto de condiciones, por ejemplo, la existencia en un tipo especial de dominio, la asociación con un operador diferencial muy particular , o la satisfacción de un conjunto preciso de condiciones de contorno. Uno de los ejemplos más comunes de este tipo puede encontrarse en las notas de, por ejemplo, Speck, donde se define una función de Green que satisface para los puntos y para todos los puntos situados en la frontera de (Speck 2011). Esta definición particular presenta un núcleo integral correspondiente a la solución de una ecuación de Poisson generalizada y, por tanto, se enfrentaría a limitaciones obvias al ser adaptada a un entorno más general. Por otro lado, estos ejemplos no están exentos de ventajas. En el caso del ejemplo de Poisson generalizado anterior, por ejemplo, cada una de estas funciones de Green puede dividirse de modo que

(14)

donde y para el laplaciano regular (Hartman 2013). En tales situaciones, se conoce como la solución fundamental de la ecuación diferencial subyacente y se conoce como su solución regular; como tal, y se llaman a veces las partes fundamental y regular de , respectivamente.

Varias propiedades fundamentales de una función de Green general se deducen inmediatamente (o casi) de su definición y se trasladan a todos los casos particulares. Por ejemplo, si el núcleo del operador no es trivial, entonces puede haber varias funciones de Green asociadas a un solo operador; como resultado, uno debe mostrar precaución cuando se refiere a «la» función de Green. Las funciones de Green satisfacen una simetría adyacente en sus dos argumentos de modo que

(15)

donde aquí, se define como la solución de la ecuación

(16)

Aquí, es el adjunto de . Un corolario inmediato de este hecho es que para los operadores autoadjuntos , es simétrico:

(17)

Esta identidad suele llamarse principio de reciprocidad y dice, en términos físicos, que la respuesta en causada por una fuente unitaria en es la misma que la respuesta en debida a una fuerza unitaria en (Stakgold 1979).

La propiedad esencial de cualquier función de Green es que proporciona una forma de describir la respuesta de una solución de ecuación diferencial arbitraria a algún tipo de término fuente en presencia de algún número de condiciones de contorno (Arfken et al. 2012). Algunos autores consideran que una función de Green tiene un papel más o menos análogo en la teoría de las ecuaciones diferenciales parciales que las series de Fourier en la solución de las ecuaciones diferenciales ordinarias (Mikula y Kos 2006).

Para escenarios más abstractos, existen varios conceptos que sirven como análogos específicos del contexto a la noción de función de Green. Por ejemplo, en el análisis funcional, a menudo es útil considerar una llamada función de Green generalizada que tiene muchas propiedades análogas cuando se integra de forma abstracta contra los funcionales en lugar de las funciones. De hecho, tales generalizaciones han dado lugar a una rama completamente análoga del análisis teórico de las EDP y son en sí mismas el centro de una gran cantidad de investigación.