Filtrado bilineal e interpolación bilineal

Mira la imagen de abajo. ¿Puedes calcular los valores en los puntos A,B y C?

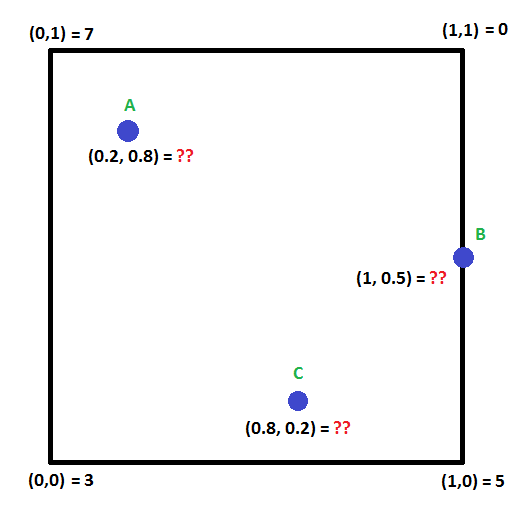
Hay una técnica para hacer esto llamada interpolación bilineal que extiende la idea de interpolación lineal a dos dimensiones.

Para calcular la interpolación bilineal, basta con hacer una interpolación lineal en un eje y luego en el otro.

Mira estos ejemplos:

Punto A
El punto A tiene una coordenada de (0,2,0,8). Comencemos con el eje X.

Primero, haremos la interpolación a través de la parte superior del cuadrado en el eje X. Eso significa que tenemos que recorrer el 0,2 (20%) del camino de 7 a 0. Ese 0,2 es nuestra coordenada del eje X. Para calcular esto hacemos lo siguiente:
7 + (0-7) * 0,2 = 5,6

A continuación, haremos la interpolación a través de la parte inferior del cuadrado en el eje X. Así que, de forma similar a lo anterior, recorreremos el 0,2 (20%) del camino del 3 al 5. Para calcular esto hacemos lo siguiente:
3 + (5-3) * 0,2 = 3,4

Ahora que hemos interpolado a través de nuestro eje X necesitamos interpolar a través de nuestro eje Y. Ahora vamos a recorrer 0,8 (80%) del camino desde nuestro valor inferior (el valor de Y = 0), hasta nuestro valor superior (el valor de Y = 1). El valor inferior es la interpolación inferior que hicimos (3,4) y el valor superior es la interpolación superior que hicimos (5,6).

Así que tenemos que recorrer 0,8 (80%) del camino desde 3,4 hasta 5,6. Para calcularlo hacemos lo siguiente:
3,4 + (5,6 – 3,4) * 0,8 = 5,16

Entonces, el valor en el punto A es 5,16. La imagen de abajo debería ayudar a explicar visualmente el proceso por el que pasamos.

Punto B

El punto B tiene unas coordenadas de (1,0,0,5).

Empecemos con la interpolación del eje X de nuevo (¡aunque podrías empezar fácilmente con el Y primero si quisieras! Terminarías con el mismo resultado).

Haciendo la interpolación del eje X a través de la parte superior, tenemos que ir 1,0 (100%) del camino de 7 a 0. Estoy seguro de que puedes adivinar cuál es la respuesta, pero aquí se calcula:
7 + (0-7) * 1,0 = 0

De manera similar, vamos a hacer la interpolación del eje X a través de la parte inferior. Tenemos que ir 1,0 (100%) del camino de 3 a 5.
3 + (5-3) * 1,0 = 5

Luego viene la interpolación del eje Y. Tenemos que ir 0,5 (50%) del camino de 5 a 0.
5 + (0-5) * 0,5 = 2,5

Ahí vamos, el valor en el punto B es 2,5. Eso también debería tener sentido mirando el diagrama. Es básicamente una interpolación lineal entre 5 y 0, y está a medio camino entre ellos, así que intuitivamente, la respuesta 2,5 debería tener sentido.

Punto C

El punto C tiene una coordenada de (0,8,0,2).

Una vez más, vamos a hacer la interpolación del eje X a través de la parte superior de la caja. Necesitamos ir 0.8 (80%) del camino de 7 a 0.
7 + (0-7) * 0.8 = 1.4

Entonces, necesitamos hacer la interpolación del eje x a través de la parte inferior de la caja. Tenemos que ir 0,8 (80%) del camino de 3 a 5.
3 + (5-3) * 0,8 = 4,6

Por último, la interpolación del eje y. Tenemos que pasar 0,2 (20%) de 4,6 a 1,4.
4,6 + (1,4-4,6) * 0,2 = 3,96

El valor del punto C es 3.96

Filtrado bilineal

Aunque la interpolación bilineal es útil si tienes una cuadrícula de datos en la que quieres interpolar valores (como un campo de altura que representa el terreno…), donde realmente brilla en el desarrollo de juegos es en el filtrado bilineal de texturas.

Básicamente, cuando tienes una coordenada de textura que no se alinea perfectamente con el centro de un píxel en la textura (porque hay un resto), utiliza la parte fraccional de la coordenada dentro de ese píxel para hacer una interpolación bilineal entre los 4 píxeles involucrados para llegar al color final del píxel. Hace la interpolación bilineal en cada uno de los canales: Rojo, Verde, Azul y Alfa.

¡El resultado final es bastante bueno! Echa un vistazo a la imagen de abajo para verlo en acción en una textura a la que le hemos hecho un zoom demasiado grande. El lado izquierdo utiliza el filtrado bilineal, mientras que el lado derecho no, y sólo muestra el píxel más cercano.

Consecuentemente, el filtrado bilineal de la textura tiene que hacer 4 lecturas de píxeles para poder interpolar entre ellos, en lugar de una sola lectura de píxeles como cuando se hace el muestreo de píxeles más cercanos. Más lecturas de píxeles = más sobrecarga, y no es tan barato (computacionalmente) para usar.

Enlaces

Para algunas personas que están leyendo esto, esta información es bastante básica y usted podría preguntarse por qué me molesté en escribir sobre ello. Mira el siguiente post para algo un poco extraño en relación con el filtrado bilineal. Esto era necesario como un trampolín para la siguiente cosa que quiero mostrar a ustedes 😛

Wikipedia: Interpolación lineal

Wikipedia: Interpolación Bilineal

Wikipedia: Filtrado bilineal

El lado oscuro del filtrado bilineal

Consulta estos enlaces para obtener información más profunda sobre algunas deficiencias (y algunas soluciones) del muestreo bilineal basado en hardware:
iq: interpolación por hardware
iq: interpolación de textura mejorada