9.5 – Identificación de puntos de datos influyentes

En esta sección, aprendemos las siguientes dos medidas para identificar puntos de datos influyentes:

• Diferencia de ajustes (DFFITS)
• Distancias de Cook

La idea básica detrás de cada una de estas medidas es la misma, a saber, eliminar las observaciones de una en una, cada vez volviendo a ajustar el modelo de regresión en las n-1 observaciones restantes. A continuación, comparamos los resultados utilizando todas las n observaciones con los resultados con la i-ésima observación eliminada para ver qué influencia tiene la observación en el análisis. Analizado como tal, somos capaces de evaluar el impacto potencial que cada punto de datos tiene en el análisis de regresión.

Diferencia en los ajustes (DFFITS)

La diferencia en los ajustes para la observación i, denotada DFFITSi, se define como:

Como puede ver, el numerador mide la diferencia en las respuestas predichas obtenidas cuando el iésimo punto de datos se incluye y se excluye del análisis. El denominador es la desviación estándar estimada de la diferencia en las respuestas predichas. Por lo tanto, la diferencia en los ajustes cuantifica el número de desviaciones estándar que cambia el valor ajustado cuando se omite el i-ésimo punto de datos.

Se considera que una observación es influyente si el valor absoluto de su valor DFFITS es mayor que:

\N

donde, como siempre, n = el número de observaciones y k = el número de términos predictores (es decir, el número de parámetros de regresión excluyendo el intercepto). Es importante tener en cuenta que no se trata de una regla rígida, sino más bien de una guía. No es difícil encontrar diferentes autores que utilicen una pauta ligeramente diferente. Por lo tanto, a menudo prefiero una directriz mucho más subjetiva, como que un punto de datos se considera influyente si el valor absoluto de su valor DFFITS sobresale como un pulgar dolorido de los otros valores DFFITS. Por supuesto, esto es un juicio cualitativo, tal vez como debería ser, ya que los valores atípicos, por su propia naturaleza, son cantidades subjetivas.

Ejemplo #2 (de nuevo). Comprobemos la diferencia en la medida de los ajustes para este conjunto de datos (influence2.txt):

Regresando y en x y solicitando la diferencia de ajustes, obtenemos la siguiente salida de software:

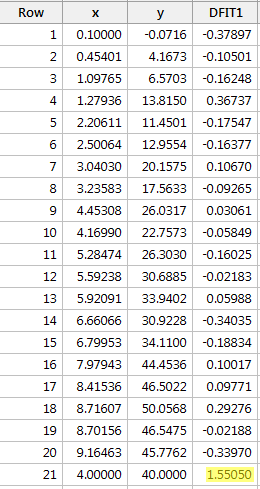
Usando la pauta objetiva definida anteriormente, consideramos que un punto de datos es influyente si el valor absoluto de su valor DFFITS es mayor que:

Sólo un punto de datos -el rojo- tiene un valor DFFITS cuyo valor absoluto (1.55050) es superior a 0,82. Por tanto, basándonos en esta pauta, consideraríamos influyente el punto de datos rojo.

Ejemplo nº 3 (de nuevo). Comprobemos la medida de diferencia de ajustes para este conjunto de datos (influence3.txt):

Regresando y en x y solicitando la diferencia de ajustes, obtenemos la siguiente salida de software:

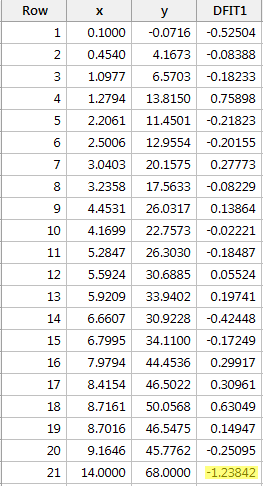
Usando la pauta objetiva definida anteriormente, consideramos que un punto de datos es influyente si el valor absoluto de su valor DFFITS es mayor que:

Sólo un punto de datos -el rojo- tiene un valor DFFITS cuyo valor absoluto (1.23841) es superior a 0,82. Por lo tanto, basándonos en esta directriz, consideraríamos que el punto de datos rojo es influyente.

Cuando estudiamos este conjunto de datos al principio de esta lección, decidimos que el punto de datos rojo no afectaba demasiado al análisis de regresión. Sin embargo, aquí, la diferencia en la medida de ajuste sugiere que sí es influyente. ¿Qué ocurre aquí? Todo se reduce a reconocer que todas las medidas de esta lección son sólo herramientas que señalan puntos de datos potencialmente influyentes para el analista de datos. Al final, el analista debe analizar el conjunto de datos dos veces, una con los puntos de datos marcados y otra sin ellos. Si los puntos de datos alteran significativamente el resultado del análisis de regresión, entonces el investigador debe informar de los resultados de ambos análisis.

Por cierto, en este ejemplo, si utilizamos la directriz más subjetiva de si el valor absoluto del valor DFFITS sobresale como un pulgar dolorido, es probable que no consideremos el punto de datos rojo como influyente. Después de todo, el siguiente valor DFFITS más grande (en valor absoluto) es 0,75898. Este valor DFFITS no es tan diferente del valor DFFITS de nuestro punto de datos «influyente».

Ejemplo nº 4 (de nuevo). Comprobemos la medida de diferencia de ajustes para este conjunto de datos (influence4.txt):

Regresando y en x y solicitando la diferencia de ajustes, obtenemos la siguiente salida de software:

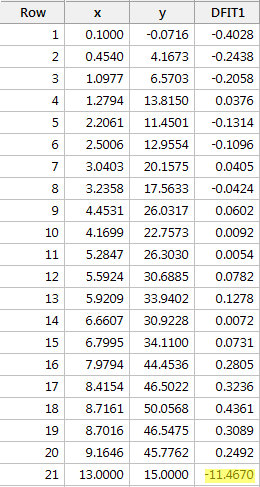
Usando la pauta objetiva definida anteriormente, volvemos a considerar que un punto de datos es influyente si el valor absoluto de su valor DFFITS es mayor que:

¿Qué opinas? ¿Hay algún valor DFFITS que destaque como un pulgar dolorido? Errr – el valor DFFITS del punto de datos rojo (-11,4670 ) es ciertamente de una magnitud diferente a todos los demás. En este caso, no debería haber ninguna duda de que el punto de datos rojo es influyente.

Distancia de Cook

En este punto, la medida de la distancia de Cook, denominada Di, se define como:

.\N]

Parece un poco desordenado, pero lo principal es reconocer que Di de Cook depende tanto del residuo, ei (en el primer término), como del apalancamiento, hii (en el segundo término). Es decir, tanto el valor x como el valor y del punto de datos desempeñan un papel en el cálculo de la distancia de Cook.

En resumen:

• Di resume directamente cuánto cambian todos los valores ajustados cuando se elimina la i-ésima observación.
• Un punto de datos que tiene un Di grande indica que el punto de datos influye fuertemente en los valores ajustados.

Investiguemos qué significa exactamente esa primera afirmación en el contexto de algunos de nuestros ejemplos.

Ejemplo #1 (de nuevo). Recordará que el gráfico de estos datos (influence1.txt) sugiere que no hay valores atípicos ni puntos de datos influyentes para este ejemplo:

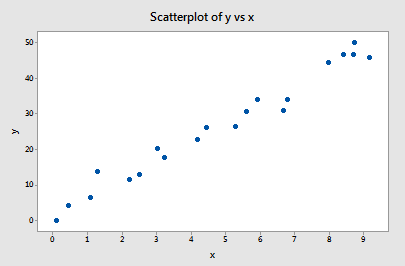
Si hacemos una regresión de y sobre x utilizando todos los n = 20 puntos de datos, determinamos que el coeficiente de intercepción estimado b0 = 1,732 y el coeficiente de pendiente estimado b1 = 5,117. Si eliminamos el primer punto de datos del conjunto de datos y realizamos la regresión de y sobre x utilizando los n = 19 puntos de datos restantes, determinamos que el coeficiente de intercepción estimado b0 = 1,732 y el coeficiente de pendiente estimado b1 = 5,1169. Como es de esperar, las estimaciones no cambian mucho al eliminar un punto de datos. Continuando este proceso de eliminar cada punto de datos uno a la vez, y trazando las pendientes estimadas resultantes (b1) frente a los interceptos estimados (b0), obtenemos:

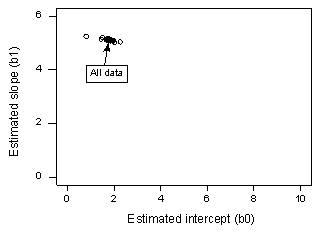
El punto negro sólido representa los coeficientes estimados basados en todos los n = 20 puntos de datos. Los círculos abiertos representan cada uno de los coeficientes estimados obtenidos al eliminar cada punto de datos de uno en uno. Como se puede ver, los coeficientes estimados están todos agrupados independientemente de qué punto de datos se elimine, si es que se elimina alguno. Esto sugiere que ningún punto de datos influye indebidamente en la función de regresión estimada o, a su vez, en los valores ajustados. En este caso, esperaríamos que todas las medidas de distancia de Cook, Di, fueran pequeñas.

Ejemplo #4 (de nuevo). Puede recordar que el gráfico de estos datos (influence4.txt) sugiere que un punto de datos es influyente y un valor atípico para este ejemplo:

Si hacemos una regresión de y sobre x utilizando todos los n = 21 puntos de datos, determinamos que el coeficiente de intercepción estimado b0 = 8,51 y el coeficiente de pendiente estimado b1 = 3,32. Si eliminamos el punto de datos rojo del conjunto de datos y realizamos la regresión de y sobre x utilizando los n = 20 puntos de datos restantes, determinamos que el coeficiente de intercepción estimado b0 = 1,732 y el coeficiente de pendiente estimado b1 = 5,1169. Las estimaciones cambian sustancialmente al eliminar un punto de datos. Continuando este proceso de eliminar cada punto de datos uno a la vez, y trazando las pendientes estimadas resultantes (b1) frente a los interceptos estimados (b0), obtenemos:

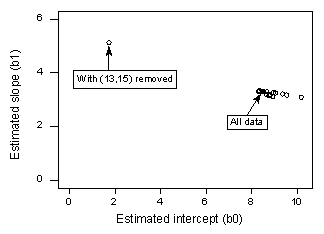
De nuevo, el punto negro sólido representa los coeficientes estimados basados en todos los n = 21 puntos de datos. Los círculos abiertos representan cada uno de los coeficientes estimados obtenidos al eliminar cada punto de datos de uno en uno. Como se puede ver, a excepción del punto de datos rojo (x = 13, y = 15), los coeficientes estimados están todos agrupados independientemente de qué punto de datos se elimine, si es que se elimina alguno. Esto sugiere que el punto de datos rojo es el único punto de datos que influye indebidamente en la función de regresión estimada y, a su vez, en los valores ajustados. En este caso, esperaríamos que la medida de distancia de Cook, Di, para el punto de datos rojo fuera grande y que las medidas de distancia de Cook, Di, para los puntos de datos restantes fueran pequeñas.

Usando las medidas de distancia de Cook. La belleza de los ejemplos anteriores es la capacidad de ver lo que está pasando con gráficos simples. Por desgracia, no podemos confiar en los gráficos simples en el caso de la regresión múltiple. En su lugar, debemos confiar en las directrices para decidir cuándo una medida de distancia de Cook es lo suficientemente grande como para justificar el tratamiento de un punto de datos como influyente.

Aquí están las directrices comúnmente utilizadas:

• Si Di es mayor que 0,5, entonces el i-ésimo punto de datos es digno de mayor investigación, ya que puede ser influyente.
• Si Di es mayor que 1, entonces es muy probable que el i-ésimo punto de datos sea influyente.
• O, si Di sobresale como un pulgar dolorido de los otros valores Di, es casi seguro que es influyente.

Ejemplo #2 (de nuevo). Comprobemos la medida de distancia de Cook para este conjunto de datos (influence2.txt):

Regresando y en x y solicitando las medidas de distancia de Cook, obtenemos la siguiente salida de software:

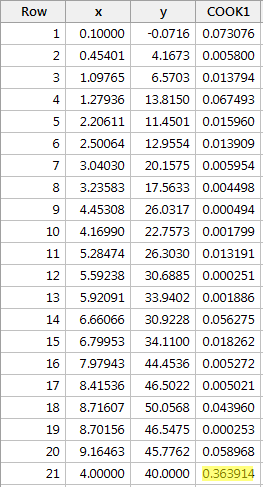
La medida de distancia de Cook para el punto de datos rojo (0,363914) destaca un poco en comparación con las otras medidas de distancia de Cook. Sin embargo, la medida de distancia de Cook para el punto de datos rojo es inferior a 0,5. Por lo tanto, basándonos en la medida de distancia de Cook, no clasificaríamos el punto de datos rojo como influyente.

Ejemplo #3 (de nuevo). Comprobemos la medida de distancia de Cook para este conjunto de datos (influence3.txt):

Regresando y en x y solicitando las medidas de distancia de Cook, obtenemos la siguiente salida de software:

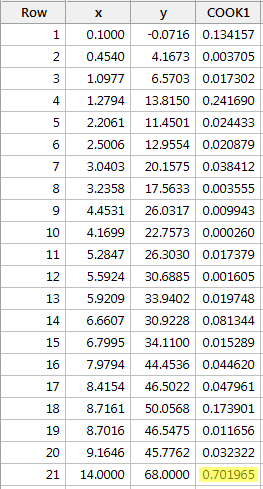
La medida de distancia de Cook para el punto de datos rojo (0,701965) destaca un poco en comparación con las otras medidas de distancia de Cook. Aún así, la medida de distancia de Cook para el punto de datos rojo es mayor que 0,5 pero menor que 1. Por lo tanto, basándonos en la medida de distancia de Cook, quizás investigaríamos más pero no necesariamente clasificaríamos el punto de datos rojo como influyente.

Ejemplo #4 (de nuevo). Comprobemos la medida de distancia de Cook para este conjunto de datos (influence4.txt):

Regresando y en x y solicitando las medidas de distancia de Cook, obtenemos la siguiente salida de software:

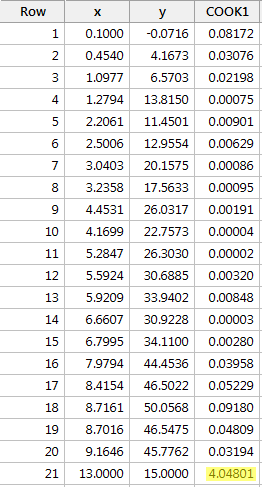
En este caso, la medida de distancia de Cook para el punto de datos rojo (4.04801) destaca sustancialmente en comparación con las otras medidas de distancia de Cook. Además, la medida de distancia de Cook para el punto de datos rojo es mayor que 1. Por lo tanto, basándonos en la medida de distancia de Cook -y no es sorprendente- clasificaríamos el punto de datos rojo como influyente.

Un método alternativo para interpretar la distancia de Cook que se utiliza a veces es relacionar la medida con la distribución F(k+1, n-k-1) y encontrar el valor del percentil correspondiente. Si este percentil es inferior a un 10 o 20 por ciento, el caso tiene poca influencia aparente en los valores ajustados. En cambio, si está cerca del 50% o incluso más, el caso tiene una gran influencia. (Cualquier cosa «entre medias» es más ambigua.)