Einführung in die Dekonvolution

Die Dekonvolution ist eine rechenintensive Bildverarbeitungstechnik, die zunehmend zur Verbesserung des Kontrasts und der Auflösung digitaler Bilder eingesetzt wird, die mit dem Mikroskop aufgenommen wurden. Die Grundlagen basieren auf einer Reihe von Methoden, die darauf abzielen, die Unschärfe zu beseitigen oder umzukehren, die in Mikroskopbildern durch die begrenzte Apertur des Objektivs entsteht.

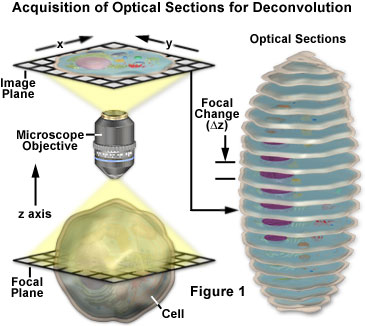
Nahezu jedes Bild, das mit einem digitalen Fluoreszenzmikroskop erfasst wird, kann dekonvolutioniert werden, und es werden mehrere neue Anwendungen entwickelt, bei denen Dekonvolutionstechniken auf Durchlichtbilder angewandt werden, die unter einer Vielzahl von Strategien zur Kontraststeigerung erfasst wurden. Zu den am besten geeigneten Objekten für eine Verbesserung durch Dekonvolution gehören dreidimensionale Montagen, die aus einer Reihe optischer Schnitte erstellt werden.

Die grundlegenden Konzepte für die Erfassung von Z-Serien-Bildern für die Dekonvolution-Analyse sind in Abbildung 1 schematisch dargestellt. Es wird eine Reihe von Bildern der Probe aufgenommen, die jeweils entlang der z-Achse leicht gegeneinander verschoben sind. Diese Änderung der Fokusebene führt zu einem leicht veränderten Bild, wobei subtile Änderungen durch unscharfes Licht von oberhalb und unterhalb der aktuellen z-Ebene verursacht werden. Bei der Entfaltungsanalyse wird die gesamte z-Reihe analysiert, um einen klareren, höher aufgelösten Datensatz zu erstellen, der nicht durch unscharfe Fluoreszenz verfälscht wird.

Die Entfaltung wird oft als gute Alternative zum konfokalen Mikroskop vorgeschlagen, da beide Techniken versuchen, die Auswirkungen unscharfer Fluoreszenz auf das endgültige Bild zu minimieren. Dies ist nicht ganz richtig, denn Bilder, die mit einer Lochblende in einem konfokalen Mikroskop aufgenommen wurden, profitieren von der Entfaltungsbearbeitung. Bei der konfokalen Mikroskopie wird verhindert, dass unscharfes Licht erkannt wird, indem zwischen Objektiv und Detektor eine Lochblende angebracht wird, durch die nur fokussierte Lichtstrahlen hindurchtreten können. Im Gegensatz dazu lassen Weitfeldmikroskope unscharfes Licht direkt zum Detektor durch. Auf die resultierenden Bilder wird dann eine Entfaltung angewandt, um das unscharfe Licht entweder zu subtrahieren oder es wieder seiner Quelle zuzuordnen. Die konfokale Mikroskopie eignet sich besonders gut für die Untersuchung dicker Proben wie Embryos oder Tussies, während sich die Weitwinkeldekonvolution als leistungsfähiges Werkzeug für die Abbildung von Proben mit extrem geringer Lichtintensität erwiesen hat. Diese Werkzeuge können sogar kombiniert werden, um das Rauschen in Bildern zu reduzieren, die mit einem konfokalen Mikroskop aufgenommen wurden. Die meisten in der Literatur beschriebenen Entfaltungsexperimente beziehen sich jedoch auf Bilder, die mit einem Standard-Weitfeld-Fluoreszenzmikroskop aufgenommen wurden.

Quellen der Bildverschlechterung

Die Bildverschlechterung kann in vier unabhängige Quellen unterteilt werden: Rauschen, Streuung, Blendung und Unschärfe. Abbildung 2 zeigt Beispiele für die visuellen Auswirkungen jeder dieser Quellen auf ein und dasselbe Bild.

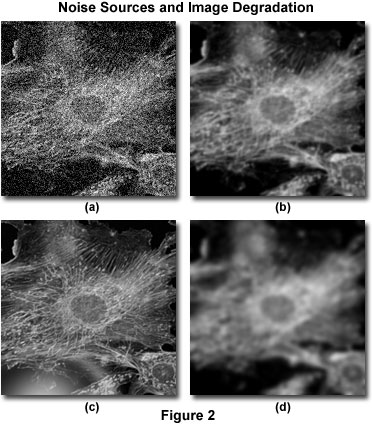
Rauschen kann als eine quasi-zufällige Störung von Details in einem Bild beschrieben werden, die (in ihrer schwersten Form) das Aussehen von weißem Rauschen oder Salz-und-Pfeffer-Rauschen hat, ähnlich dem, was man bei schlechtem Empfang im Fernsehen sieht (Abbildung 2(a)). Diese Art von Rauschen wird als „quasi-zufällig“ bezeichnet, weil die statistische Verteilung vorhergesagt werden kann, wenn die Mechanik der Quelle bekannt ist. In der digitalen Mikroskopie ist die Hauptquelle des Rauschens entweder das Signal selbst (oft als Photonenschussrauschen bezeichnet) oder das digitale Bildgebungssystem. Die Mechanik beider Rauschquellen ist bekannt, und daher ist auch die statistische Verteilung des Rauschens bekannt. Das signalabhängige Rauschen kann durch eine Poisson-Verteilung charakterisiert werden, während das vom Bildgebungssystem verursachte Rauschen oft einer Gauß-Verteilung folgt. Da die Quelle und die Verteilung des allgemeinen Rauschens in digitalen Bildern so gut bekannt sind, kann es leicht durch die Anwendung geeigneter Bildfilter entfernt werden, die in der Regel in den meisten Entfaltungssoftwarepaketen als optionale „Vorverarbeitungs“-Routine enthalten sind.

Streuung wird gewöhnlich als eine zufällige Störung des Lichts bezeichnet, die durch Änderungen des Brechungsindex in einer Probe verursacht wird. Der Nettoeffekt der Streuung ist eine wirklich zufällige Störung der Bilddetails, wie in Abbildung 2(b) zu sehen ist. Obwohl noch keine völlig zufriedenstellende Methode zur Vorhersage der Streuung in einer bestimmten Probe entwickelt wurde, hat sich gezeigt, dass das Ausmaß der Streuung in hohem Maße von der Probendicke und den optischen Eigenschaften der Probe und der umgebenden Einbettungsmaterialien abhängt. Die Streuung nimmt sowohl mit der Probendicke als auch mit der Heterogenität des Brechungsindexes der inneren Komponenten einer Probe zu.

Ähnlich wie bei der Streuung handelt es sich bei der Blendung um eine zufällige Störung des Lichts, die jedoch in den optischen Elementen (Linsen, Filter, Prismen usw.) des Mikroskops und nicht in der Probe auftritt. Der Grad der Blendung in einem modernen Mikroskop wurde durch die Verwendung von Linsen und Filtern mit Antireflexionsbeschichtungen sowie durch die Verfeinerung von Linsenformungstechniken, optischen Kitten und Glasrezepturen minimiert. Abbildung 2(c) zeigt die Auswirkungen unkontrollierter Blendung.

Unschärfe wird durch eine nicht zufällige Ausbreitung des Lichts beschrieben, die beim Durchgang durch den optischen Pfad des Abbildungssystems auftritt (Abbildung 2(d)). Die wichtigste Quelle der Unschärfe ist die Beugung, und ein Bild, dessen Auflösung nur durch die Unschärfe begrenzt wird, gilt als beugungsbegrenzt. Dies stellt eine intrinsische Grenze jedes Abbildungssystems dar und ist der entscheidende Faktor bei der Beurteilung der Auflösungsgrenze eines optischen Systems. Glücklicherweise stehen ausgefeilte Modelle der Unschärfe in einem optischen Mikroskop zur Verfügung, mit deren Hilfe die Quelle der unscharfen Photonen bestimmt werden kann. Dies ist die Grundlage für die Dekonvolution. Wegen seiner grundlegenden Bedeutung für die Entfaltung wird das theoretische Modell der Unschärfe in anderen Teilen dieses Abschnitts ausführlicher behandelt. Es sollte jedoch betont werden, dass alle bildgebenden Systeme unabhängig von den anderen Formen der Bildverschlechterung, die durch die Probe oder die begleitende Instrumentenelektronik verursacht werden, Unschärfe erzeugen. Genau diese Unabhängigkeit der optischen Unschärfe von anderen Arten der Verschlechterung ermöglicht die Beseitigung der Unschärfe durch Entfaltungstechniken.

Die Wechselwirkung von Licht mit Materie ist der primäre physikalische Ursprung von Streuung, Blendung und Unschärfe. Die Zusammensetzung und Anordnung der Moleküle in einem bestimmten Material (sei es Glas, Wasser oder Protein) verleiht jedoch jedem Material seine eigenen optischen Eigenschaften. Für die Zwecke der Entfaltung unterscheiden sich Streuung, Blendung und Unschärfe durch den Ort, an dem sie auftreten, und durch die Möglichkeit, ein mathematisches Modell für diese Phänomene zu erstellen. Da es sich bei der Streuung um ein örtlich begrenztes, unregelmäßiges Phänomen handelt, das in der Probe auftritt, hat es sich als schwierig erwiesen, es zu modellieren. Da die Unschärfe hingegen eine Funktion des optischen Systems des Mikroskops (hauptsächlich des Objektivs) ist, kann sie relativ einfach modelliert werden. Ein solches Modell macht es möglich, den Unschärfeprozess mathematisch umzukehren, und die Dekonvolution nutzt dieses Modell, um die Unschärfe umzukehren oder zu beseitigen.

Die Punktspreizfunktion

Das in der theoretischen Optik entwickelte Modell für die Unschärfe basiert auf dem Konzept einer dreidimensionalen Punktspreizfunktion (PSF). Dieses Konzept ist von grundlegender Bedeutung für die Dekonvolution und sollte klar verstanden werden, um Abbildungsartefakte zu vermeiden. Die Punktausbreitungsfunktion basiert auf einer unendlich kleinen punktförmigen Lichtquelle, die ihren Ursprung im Probenraum (Objekt) hat. Da das Abbildungssystem des Mikroskops nur einen Bruchteil des von diesem Punkt ausgehenden Lichts auffängt, kann es das Licht nicht zu einem perfekten dreidimensionalen Bild des Punkts fokussieren. Stattdessen erscheint der Punkt aufgeweitet und in einem dreidimensionalen Beugungsmuster verteilt. Somit ist die Punktausbreitungsfunktion formal definiert als das dreidimensionale Beugungsmuster, das von einer idealen Punktlichtquelle erzeugt wird.

Abhängig vom verwendeten Abbildungsmodus (Weitfeld, konfokal, Durchlicht) hat die Punktausbreitungsfunktion eine unterschiedliche und einzigartige Form und Kontur. Bei einem Weitfeld-Fluoreszenzmikroskop ähnelt die Form der Punktausbreitungsfunktion einem länglichen „Fußball“ aus Licht, der von einer Fackel mit sich erweiternden Ringen umgeben ist. Um die Punktausbreitungsfunktion in drei Dimensionen zu beschreiben, wird üblicherweise ein Koordinatensystem mit drei Achsen (x, y und z) verwendet, wobei x und y parallel zur Fokusebene der Probe und z parallel zur optischen Achse des Mikroskops liegen. In diesem Fall erscheint die Punktausbreitungsfunktion als eine Reihe konzentrischer Ringe in der x-y-Ebene und ähnelt einer Sanduhr in der x-z- und y-z-Ebene (wie in Abbildung 3 dargestellt). Ein x-y-Schnitt durch das Zentrum der Breitfeld-Punktspreizfunktion zeigt eine Reihe konzentrischer Ringe: die so genannte Airy-Scheibe, auf die in Texten über klassische optische Mikroskopie häufig Bezug genommen wird.

In Abbildung 3 sind zwei x-z-Projektionen von Punktspreizfunktionen dargestellt, die unterschiedliche Grade sphärischer Aberration zeigen. Die optische Achse ist parallel zur vertikalen Achse des Bildes. Die Punktspreizungsfunktion auf der linken Seite weist eine minimale sphärische Aberration auf, während die rechte Funktion einen erheblichen Grad an Aberration zeigt. Man beachte, dass die axiale Asymmetrie und die Verbreiterung des zentralen Knotens entlang der optischen Achse im rechten Bild zu einer verminderten axialen Auflösung und einer Verwischung des Signals führt. Theoretisch ist die Größe der Punktstreufunktion unendlich, und die summierte Gesamtintensität des Lichts in den fokusfernen Ebenen ist gleich der summierten Intensität im Fokus. Die Lichtintensität nimmt jedoch schnell ab und ist schließlich nicht mehr von Rauschen zu unterscheiden. In einer unverzerrten Punktausbreitungsfunktion, die mit einem Ölimmersionsobjektiv mit hoher numerischer Apertur (1,40) aufgenommen wurde, verteilt sich das Licht, das in der Fokusebene 0,2 Quadratmikrometer einnimmt, über das 90-fache dieser Fläche in der Ebene 1 Mikrometer über und unter dem Fokus. Die Probe, die zur Aufnahme dieser Punktausbreitungsfunktion verwendet wurde, war ein fluoreszierendes Kügelchen mit einem Durchmesser von 0,1 Mikrometer, das in Glycerin (Brechungsindex 1,47) eingebettet war, wobei die Immersionsöle die in der Abbildung angegebenen Brechungsindizes aufwiesen.

Eine wichtige Überlegung ist, wie die Punktausbreitungsfunktion die Bildbildung im Mikroskop beeinflusst. Das theoretische Modell der Bildentstehung behandelt die Punktspreizungsfunktion als die Grundeinheit eines Bildes. Mit anderen Worten: Die Punktspreizungsfunktion ist für das Bild das, was der Ziegelstein für das Haus ist. Das Beste, was ein Bild jemals sein kann, ist eine Ansammlung von Punktverteilungsfunktionen, und eine Erhöhung der Vergrößerung ändert nichts an dieser Tatsache. In einem bekannten Lehrbuch der theoretischen Optik (Born und Wolf: Principles of Optics) heißt es: „Es ist unmöglich, Details, die im Primärbild nicht vorhanden sind, durch eine stärkere Vergrößerung des Okulars hervorzuheben, denn jedes Element des Primärbildes ist ein kleines Beugungsmuster, und das eigentliche Bild, wie es durch das Okular gesehen wird, ist nur die Gesamtheit der vergrößerten Bilder dieser Muster“.

Betrachten wir als Beispiel eine Population von Fluoreszenzkügelchen mit geringer Auflösung, die zwischen einem Deckglas und einem Objektträger liegen. Ein scharfes Bild dieser Probe zeigt eine Wolke von Punkten, die eigentlich eine Scheibe ist, die von winzigen Ringen umgeben ist (tatsächlich eine Airy-Scheibe; siehe Abbildung 4(a)). Wenn diese Probe etwas aus dem Fokus entfernt wird, erscheint ein größerer Satz konzentrischer Ringe an der Stelle, an der sich jeder Punkt im fokussierten Bild befand (Abbildung 4(b)). Wenn ein dreidimensionales Bild dieser Probe aufgenommen wird, wird eine vollständige Punktspreizungsfunktion für jede Perle aufgezeichnet. Die Punktausbreitungsfunktion beschreibt, was mit jeder punktförmigen Lichtquelle geschieht, nachdem sie das Bildgebungssystem durchlaufen hat.

Der soeben beschriebene Unschärfeprozess wird mathematisch als eine Faltung modelliert. Die Faltungsoperation beschreibt die Anwendung der Punktspreizfunktion auf jeden Punkt der Probe: Das von jedem Punkt des Objekts emittierte Licht wird mit der Punktspreizfunktion gefaltet, um das endgültige Bild zu erzeugen. Leider führt diese Faltung dazu, dass Punkte in der Probe zu unscharfen Bereichen im Bild werden. Die Helligkeit jedes Punktes im Bild ist durch die Faltungsoperation linear mit der Fluoreszenz jedes Punktes in der Probe verbunden. Da die Punktspreizfunktion dreidimensional ist, ist die Unschärfe der Punktspreizfunktion ein inhärentes dreidimensionales Phänomen. Das Bild einer beliebigen Fokusebene enthält unscharfes Licht von Punkten, die sich in dieser Ebene befinden, gemischt mit unscharfem Licht von Punkten, die aus anderen Fokusebenen stammen.

Die Situation lässt sich mit der Vorstellung zusammenfassen, dass das Bild durch eine Faltung der Probe mit der Punktspreizfunktion entsteht. Die Entfaltung kehrt diesen Prozess um und versucht, die Probe aus einem unscharfen Bild zu rekonstruieren.

Aberrationen in der Punktspreizungsfunktion

Die Punktspreizungsfunktion kann entweder theoretisch durch Verwendung eines mathematischen Beugungsmodells oder empirisch durch Aufnahme eines dreidimensionalen Bildes eines fluoreszierenden Kügelchens definiert werden (siehe Abbildung 3). Eine theoretische Punktausbreitungsfunktion hat im Allgemeinen eine axiale und radiale Symmetrie. Tatsächlich ist die Punktausbreitungsfunktion oberhalb und unterhalb der x-y-Ebene (axiale Symmetrie) und um die z-Achse (radiale Symmetrie) symmetrisch. Eine empirische Punktstreufunktion kann erheblich von der perfekten Symmetrie abweichen (wie in Abbildung 3 dargestellt). Diese Abweichung, die allgemein als Aberration bezeichnet wird, wird durch Unregelmäßigkeiten oder Fehlausrichtungen in einer beliebigen Komponente des optischen Systems verursacht, insbesondere im Objektiv, kann aber auch bei anderen Komponenten wie Spiegeln, Strahlteilern, Tubuslinsen, Filtern, Blenden und Aperturen auftreten. Je höher die Qualität der optischen Komponenten und je besser die Ausrichtung des Mikroskops ist, desto näher kommt die empirische Punktstreufunktion ihrer idealen symmetrischen Form. Sowohl die konfokale als auch die dekonvolutionäre Mikroskopie sind darauf angewiesen, dass die Punktspreizungsfunktion dem Idealfall so nahe wie möglich kommt.

Die häufigste Aberration in der optischen Mikroskopie, die jedem erfahrenen und professionellen Mikroskopiker bekannt ist, ist die sphärische Aberration. Diese Aberration äußert sich in einer axialen Asymmetrie in der Form der Punktverteilungsfunktion mit einer entsprechenden Zunahme der Größe, insbesondere entlang der z-Achse (Abbildung 3). Das Ergebnis ist ein erheblicher Verlust an Auflösung und Signalintensität. In der Praxis ist die typische Ursache für sphärische Aberration eine Diskrepanz zwischen den Brechungsindizes des Immersionsmediums der Frontlinse des Objektivs und des Einbettungsmediums, in das die Probe eingetaucht ist. Die Minimierung dieser Aberration ist von großer Bedeutung. Obwohl die Dekonvolution die verlorene Auflösung teilweise wiederherstellen kann, kann keine noch so gute Bildverarbeitung das verlorene Signal wiederherstellen.