Einführung in das konsistente Hashing

Mit dem Aufkommen verteilter Architekturen wurde Consistent Hashing zum Mainstream. Aber was ist das genau und wie unterscheidet es sich von einem Standard-Hashing-Algorithmus? Was sind die genauen Beweggründe dafür?

Zunächst werden wir die wichtigsten Konzepte beschreiben. Dann werden wir uns mit den bestehenden Algorithmen befassen, um die Herausforderungen zu verstehen, die mit konsistentem Hashing verbunden sind.

Hashing

Hashing ist der Prozess, bei dem Daten beliebiger Größe auf Werte fester Größe abgebildet werden. Jeder bestehende Algorithmus hat seine eigene Spezifikation:

• MD5 erzeugt 128-Bit-Hash-Werte.
• SHA-1 erzeugt 160-Bit-Hash-Werte.
• etc.

Hashing hat viele Anwendungen in der Informatik. Eine dieser Anwendungen ist zum Beispiel die Prüfsumme. Um die Integrität eines Datensatzes zu überprüfen, kann ein Hashing-Algorithmus verwendet werden. Ein Server hasht einen Datensatz und gibt den Hashwert an einen Client weiter. Dann hasst der Client seine Version des Datensatzes und vergleicht die Hash-Werte. Wenn sie gleich sind, sollte die Integrität überprüft werden.

Das „sollte“ ist hier wichtig. Im schlimmsten Fall kommt es zu einer Kollision. Eine Kollision liegt vor, wenn zwei unterschiedliche Daten denselben Hash-Wert haben. Nehmen wir ein Beispiel aus dem wirklichen Leben, indem wir die folgende Hash-Funktion definieren: Bei einer Person gibt sie ihr Geburtstagsdatum zurück (Tag & Monat der Geburt). Das Geburtstagsparadoxon besagt, dass bei nur 23 Personen in einem Raum die Wahrscheinlichkeit, dass zwei Personen denselben Geburtstag haben (also eine Kollision), mehr als 50 % beträgt. Daher ist die Geburtstagsfunktion wahrscheinlich keine gute Hashing-Funktion.

Als schnelle Einführung in das Hashing ist es wichtig zu verstehen, dass es im Wesentlichen darum geht, Werte über einen Bereich zu verteilen. Zum Beispiel:

• MD5 verteilt Werte über einen 128-Bit-Raum
• Eine Hashtabelle (oder Hashmap), die von einem Array mit 32 Elementen unterstützt wird, verfügt über eine interne Hash-Funktion, die Werte auf einen beliebigen Index (von 0 bis 31) verteilt.

Lastverteilung

Lastverteilung kann als der Prozess der Verteilung von Last auf Knoten definiert werden. Der Begriff Knoten ist hier austauschbar mit Server oder Instanz. Es handelt sich um eine Recheneinheit.

Lastausgleich ist ein Beispiel für Lastverteilung. Dabei geht es um die Verteilung einer Reihe von Aufgaben auf eine Reihe von Ressourcen. Zum Beispiel verwenden wir Load Balancing, um die API-Anfragen auf Webserver-Instanzen zu verteilen.

Wenn es um Daten geht, verwenden wir eher den Begriff Sharding. Ein Datenbank-Shard ist eine horizontale Partition von Daten in einer Datenbank. Ein typisches Beispiel ist eine Datenbank, die in drei Shards partitioniert ist, wobei jeder Shard eine Teilmenge der Gesamtdaten enthält.

Lastausgleich und Sharding haben einige gemeinsame Herausforderungen. Zum Beispiel die gleichmäßige Verteilung der Daten, um zu gewährleisten, dass ein Knoten im Vergleich zu den anderen nicht überlastet wird. In einigen Kontexten müssen Load Balancing und Sharding auch Aufgaben oder Daten demselben Knoten zuordnen:

• Wenn wir die Operationen für einen bestimmten Verbraucher serialisieren, d. h. eine nach der anderen abwickeln müssen, müssen wir die Anfrage an denselben Knoten weiterleiten.
• Wenn wir Daten verteilen müssen, müssen wir wissen, welcher Shard der Eigentümer für einen bestimmten Schlüssel ist.

Kommt Ihnen das bekannt vor? In diesen beiden Beispielen verteilen wir Werte über eine Domäne. Ob es sich um eine Aufgabe handelt, die auf Serverknoten verteilt wird, oder um Daten, die auf Datenbank-Shards verteilt werden, wir finden die Idee wieder, die mit Hashing verbunden ist. Dies ist der Grund, warum Hashing in Verbindung mit Lastverteilung verwendet werden kann. Sehen wir uns an, wie das geht.

Mod-n-Hashing

Das Prinzip des Mod-n-Hashings ist das folgende. Jeder Schlüssel wird mit Hilfe einer Hashing-Funktion gehasht, um eine Eingabe in eine ganze Zahl umzuwandeln. Dann wird ein Modulo auf der Grundlage der Anzahl der Knoten durchgeführt.

Betrachten wir ein konkretes Beispiel mit 3 Knoten. Hier müssen wir die Last auf der Grundlage einer Schlüsselkennung auf diese Knoten verteilen. Jeder Schlüssel wird gehasht, dann führen wir eine Modulo-Operation durch:

Der Vorteil dieses Ansatzes ist seine Zustandslosigkeit. Wir müssen keinen Zustand aufbewahren, der uns daran erinnert, dass foo an Knoten 2 weitergeleitet wurde. Dennoch müssen wir wissen, wie viele Knoten konfiguriert sind, um die Modulo-Operation anzuwenden.

Wie funktioniert der Mechanismus dann bei einer Verkleinerung oder Vergrößerung (Hinzufügen oder Entfernen von Knoten)? Wenn wir einen weiteren Knoten hinzufügen, basiert die Modulo-Operation nun auf 4 statt auf 3:

Wie wir sehen, sind die Schlüssel foo und baz nicht mehr mit demselben Knoten verbunden. Beim Mod-n-Hashing gibt es keine Garantie für die Aufrechterhaltung der Konsistenz der Schlüssel-Knoten-Zuordnung. Ist das ein Problem? Möglicherweise.

Was ist, wenn wir einen Datenspeicher implementieren, der Sharding verwendet und auf der mod-n-Strategie zur Verteilung der Daten basiert? Wenn wir die Anzahl der Knoten skalieren, müssen wir einen Rebalancing-Vorgang durchführen. Im vorherigen Beispiel bedeutet Rebalancing:

• Verschieben von foo von Knoten 2 nach Knoten 0.
• Verschieben von baz von Knoten 2 nach Knoten 3.

Was passiert nun, wenn wir Millionen oder sogar Milliarden von Daten gespeichert haben und fast alles neu ausbalancieren müssen? Wie wir uns vorstellen können, wäre dies ein aufwendiger Prozess. Daher müssen wir unsere Technik der Lastverteilung ändern, um sicherzustellen, dass beim Rebalancing:

• die Verteilung auf der Grundlage der neuen Anzahl von Knoten so gleichmäßig wie möglich bleibt.
• Die Anzahl der Schlüssel, die wir migrieren müssen, sollte begrenzt sein. Idealerweise wäre es nur 1/n Prozent der Schlüssel, wobei n die Anzahl der Knoten ist.

Das ist genau der Zweck von konsistenten Hash-Algorithmen.

Der Begriff konsistent könnte allerdings etwas verwirrend sein. Ich bin Ingenieuren begegnet, die davon ausgingen, dass solche Algorithmen einen bestimmten Schlüssel immer demselben Knoten zuordnen, auch wenn die Skalierbarkeit gegeben ist. Das ist aber nicht der Fall. Der Algorithmus muss bis zu einem bestimmten Punkt konsistent sein, damit die Verteilung gleichmäßig bleibt.

Jetzt ist es an der Zeit, sich mit einigen Lösungen zu befassen.

Rendezvous

Rendezvous war der erste Algorithmus, der zur Lösung unseres Problems vorgeschlagen wurde. Obwohl die ursprüngliche Studie, die 1996 veröffentlicht wurde, den Begriff „consistent hashing“ nicht erwähnt, bietet sie eine Lösung für die beschriebenen Probleme. Schauen wir uns eine mögliche Implementierung in Go an:

Wie funktioniert das? Wir durchlaufen jeden Knoten und berechnen seinen Hashwert. Der Hash-Wert wird von einer hash-Funktion zurückgegeben, die eine ganze Zahl auf der Grundlage eines Schlüssels (unsere Eingabe) und eines Knotenidentifikators erzeugt (der einfachste Ansatz ist die Hash-Verknüpfung der beiden Strings). Anschließend geben wir den Knoten mit dem höchsten Hash-Wert zurück. Dies ist der Grund, warum der Algorithmus auch als „highest random weight hashing“ bekannt ist.

Der größte Nachteil von Rendezvous ist seine O(n)-Zeitkomplexität, wobei n die Anzahl der Knoten ist. Es ist sehr effizient, wenn wir eine begrenzte Anzahl von Knoten benötigen. Wenn wir jedoch anfangen, Tausende von Knoten zu verwalten, kann es zu Leistungsproblemen kommen.

Ring Consistent Hash

Der nächste Algorithmus wurde 1997 von Karger et al. in diesem Papier veröffentlicht. In dieser Studie wurde der Begriff „Consistent Hashing“ zum ersten Mal erwähnt.

Er basiert auf einem Ring (einem durchgängig verbundenen Array). Obwohl es der populärste konsistente Hash-Algorithmus ist (oder zumindest der bekannteste), wird das Prinzip nicht immer gut verstanden. Tauchen wir ein.

Der erste Vorgang ist die Erstellung des Rings. Ein Ring hat eine feste Länge. In unserem Beispiel unterteilen wir ihn in 12 Teile:

Dann positionieren wir unsere Knotenpunkte. In unserem Beispiel werden wir N0, N1 und N2 definieren.

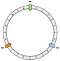
Die Knoten werden vorerst gleichmäßig verteilt. Wir werden später auf diesen Punkt zurückkommen.

Dann ist es an der Zeit, sich zu überlegen, wie man die Schlüssel darstellen kann. Zunächst brauchen wir eine Funktion f, die einen Ringindex (von 0 bis 11) auf der Grundlage eines Schlüssels zurückgibt. Dafür können wir mod-n Hashing verwenden. Da die Ringlänge konstant ist, wird uns das keine Probleme bereiten.

In unserem Beispiel werden wir 3 Schlüssel definieren: a, b und c. Wir wenden f auf jeden dieser Schlüssel an. Nehmen wir an, wir haben folgende Ergebnisse:

• f(a) = 1
• f(a) = 5
• f(a) = 7

Damit können wir die Tasten auf dem Ring so positionieren:

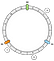
Wie ordnen wir einen bestimmten Schlüssel einem Knoten zu? Die Hauptlogik ist, sich vorwärts zu bewegen. Von einem gegebenen Schlüssel geben wir den ersten Knoten zurück, den wir beim Vorwärtsgehen als nächstes finden:

In diesem Beispiel assoziieren wir a mit N1, b und c mit N2.

Nun wollen wir sehen, wie das Rebalancing gehandhabt wird. Wir definieren einen weiteren Knoten N3. Wo sollen wir ihn positionieren? Es gibt keinen Platz mehr für eine einheitliche Gesamtverteilung. Sollen wir die Knoten umorganisieren? Nein, sonst wären wir nicht mehr konsistent, nicht wahr? Um einen Knoten zu positionieren, verwenden wir dieselbe Hashing-Funktion f, die wir eingeführt haben. Anstatt mit einem Schlüssel kann sie mit einer Knotenkennung aufgerufen werden. So wird die Position des neuen Knotens zufällig bestimmt.

Eine Frage stellt sich dann: was sollen wir mit a machen, da der nächste Knoten nicht mehr N1 ist:

Die Lösung ist die folgende: Wir müssen seine Assoziation ändern und a mit N3 assoziieren:

Wie wir bereits besprochen haben, sollte ein idealer Algorithmus im Durchschnitt 1/n Prozent der Schlüssel neu ausgleichen. Da in unserem Beispiel ein vierter Knoten hinzukommt, sollten 25 % der möglichen Schlüssel mit N3 neu assoziiert werden. Ist dies der Fall?

• N0 von den Indizes 8 bis 12: 33,3% der gesamten Schlüssel
• N1 von den Indizes 2 bis 4: 16,6% der gesamten Schlüssel
• N2 von den Indizes 4 bis 8: 33.3% der gesamten Schlüssel
• N3 von Index 0 bis 2: 16,6% der gesamten Schlüssel

Die Verteilung ist nicht gleichmäßig. Wie können wir das verbessern? Die Lösung liegt in der Verwendung virtueller Knotenpunkte

Anstatt eines einzigen Punktes pro Knotenpunkt können wir drei positionieren. Außerdem müssen wir drei verschiedene Hashing-Funktionen definieren. Jeder Knoten wird dreimal gehasht, so dass wir drei verschiedene Indizes erhalten:

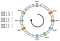
Wir können denselben Algorithmus anwenden, indem wir vorwärts gehen. Allerdings würde ein Schlüssel einem Knoten zugeordnet werden, unabhängig davon, auf welchen virtuellen Knoten er trifft.

In diesem Beispiel würde die Verteilung nun wie folgt aussehen:

• N0: 33,3%
• N1: 25%
• N2: 41,6%

Je mehr virtuelle Knoten wir pro Knoten definieren, desto gleichmäßiger sollte die Verteilung sein. Im Durchschnitt beträgt die Standardverteilung bei 100 virtuellen Knoten pro Server etwa 10 %. Bei 1000 beträgt sie etwa 3,2 %.

Dieser Mechanismus ist auch nützlich, wenn wir Knoten mit unterschiedlicher Größe haben. Wenn zum Beispiel ein Knoten so konfiguriert ist, dass er theoretisch die doppelte Last als die anderen bewältigen kann, können wir doppelt so viele virtuelle Knoten aufsetzen.

Der größte Nachteil der virtuellen Knoten ist jedoch der Speicherbedarf. Wenn wir mit Tausenden von Servern umgehen müssen, benötigen wir Megabytes an Speicher.

Bevor wir weitermachen, ist es interessant festzustellen, dass ein Algorithmus manchmal durch die Änderung eines kleinen Teils erheblich verbessert werden kann. Dies ist zum Beispiel bei einem Algorithmus der Fall, der 2017 von Google veröffentlicht wurde und sich „consistent hashing with bounded loads“ nennt. Diese Version basiert auf der gleichen Ringidee, die wir beschrieben haben. Ihr Ansatz besteht jedoch darin, bei jeder Aktualisierung (Hinzufügen/Löschen eines neuen Schlüssels oder Knotens) eine kleine Neugewichtung vorzunehmen. Diese Version übertrifft die ursprüngliche in Bezug auf die Standardabweichung mit dem Nachteil einer schlechteren Zeitkomplexität.

Jump Consistent Hash

Im Jahr 2007 veröffentlichten zwei Ingenieure von Google Jump Consistent Hash. Im Vergleich zum ringbasierten Algorithmus benötigt diese Implementierung „keinen Speicherplatz, ist schneller und sorgt für eine gleichmäßige Aufteilung des Schlüsselraums auf die Buckets sowie für eine gleichmäßige Verteilung der Arbeitslast, wenn sich die Anzahl der Buckets ändert“. Anders ausgedrückt, er verbessert die Verteilung der Arbeitslast auf die Knoten (ein Bucket ist dasselbe Konzept wie ein Knoten) ohne jeglichen Speicher-Overhead.

Hier ist der Algorithmus in C++ (7 Zeilen Code 🤯):

Beim Ring Consistent Hash betrug die Standardabweichung bei 1000 virtuellen Knoten etwa 3,2 %. Bei Jump Consistent Hash brauchen wir das Konzept der virtuellen Knoten nicht mehr. Dennoch bleibt die Standardabweichung kleiner als 0,0000001%.

Eine Einschränkung gibt es allerdings. Die Knoten müssen fortlaufend nummeriert sein. Wenn wir eine Liste von Servern foo, bar und baz haben, können wir zum Beispiel bar nicht entfernen. Wenn wir jedoch einen Datenspeicher konfigurieren, können wir den Algorithmus anwenden, um den Shard-Index auf der Grundlage der Gesamtzahl der Shards zu erhalten. Daher kann Jump Consistent Hash im Zusammenhang mit Sharding nützlich sein, aber nicht für den Lastausgleich.

Was ist der Perfect Consistent Hashing Algorithmus?

Da wir nun einige Erfahrung mit konsistentem Hashing haben, lassen Sie uns einen Schritt zurückgehen und sehen, was der perfekte Algorithmus wäre:

• Nur 1/n Prozent der Schlüssel würden im Durchschnitt neu zugeordnet werden, wobei n die Anzahl der Knoten ist.
• Eine O(n) Raumkomplexität, wobei n die Anzahl der Knoten ist.
• Eine O(1)-Zeitkomplexität pro Einfügung/Entfernung eines Knotens und pro Schlüsselsuche.
• Eine minimale Standardabweichung, um sicherzustellen, dass ein Knoten im Vergleich zu einem anderen nicht überlastet ist.
• Es würde erlauben, einem Knoten ein Gewicht zuzuordnen, um mit unterschiedlicher Knotengröße zurechtzukommen.
• Es würde beliebige Knotennamen (nicht fortlaufend nummeriert) erlauben, um sowohl Lastausgleich als auch Sharding zu unterstützen.

Leider existiert dieser Algorithmus nicht. Basierend auf dem, was wir gesehen haben:

• Rendezvous hat eine lineare Zeitkomplexität pro Lookup.
• Ringkonsistenter Hash hat eine schlechte minimale Standardabweichung ohne das Konzept der virtuellen Knoten. Mit virtuellen Knoten ist die Raumkomplexität O(n*v), wobei n die Anzahl der Knoten und v die Anzahl der virtuellen Knoten pro Knoten ist.
• Der konsistente Hash hat keine konstante Zeitkomplexität und unterstützt keine beliebigen Knotennamen.

Das Thema ist noch offen, und es gibt aktuelle Studien, die einen Blick wert sind. Zum Beispiel, die Multi-Probe konsistente Hash im Jahr 2005 veröffentlicht. Er unterstützt O(1) Raumkomplexität. Um jedoch eine Standardabweichung von ε zu erreichen, benötigt er O(1/ε) Zeit pro Lookup. Wenn wir zum Beispiel eine Standardabweichung von weniger als 0,5 % erreichen wollen, muss der Schlüssel etwa 20 Mal gehasht werden. Daher können wir eine minimale Standardabweichung erreichen, aber mit einer höheren Zeitkomplexität beim Nachschlagen.

Wie in der Einleitung erwähnt, haben sich konsistente Hashing-Algorithmen durchgesetzt. Er wird nun in unzähligen Systemen wie MongoDB, Cassandra, Riak, Akka usw. verwendet, sei es im Zusammenhang mit dem Lastausgleich oder der Verteilung von Daten. Doch wie so oft in der Informatik hat jede Lösung Kompromisse.

Wenn Sie über Kompromisse sprechen, sollten Sie einen Blick auf den hervorragenden Beitrag von Damian Gryski werfen: