Eine sanfte Einführung in das Problem der konvexen Hülle

Konvexe Rümpfe sind in vielen verschiedenen Bereichen nützlich, manchmal ganz unerwartet. In diesem Artikel erkläre ich die Grundidee der konvexen 2d-Rümpfe und wie man sie mit dem Graham-Scan findet. Wenn Sie also bereits mit dem Graham-Scan vertraut sind, dann ist dieser Artikel nichts für Sie, aber wenn nicht, dann sollte er Sie mit einigen der relevanten Konzepte vertraut machen.

Die konvexe Hülle einer Punktmenge ist definiert als das kleinste konvexe Polygon, das alle Punkte der Menge einschließt. Konvex bedeutet, dass das Polygon keine nach innen gebogene Ecke hat.

Die roten Kanten des rechten Polygons umschließen die Ecke, in der die Form konkav ist, also das Gegenteil von konvex.

Eine nützliche Art, über die konvexe Hülle nachzudenken, ist die Gummiband-Analogie. Nehmen wir an, die Punkte in der Menge wären Nägel, die aus einer flachen Oberfläche herausragen. Stellen Sie sich nun vor, was passieren würde, wenn Sie ein Gummiband nehmen und es um die Nägel spannen würden. Beim Versuch, sich wieder auf seine ursprüngliche Länge zusammenzuziehen, würde das Gummiband die Nägel umschließen und dabei die Nägel berühren, die am weitesten aus der Mitte herausragen.

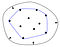
Um die resultierende konvexe Hülle im Code darzustellen, speichern wir normalerweise die Liste der Punkte, die dieses Gummiband aufrecht erhalten, d.h. die Liste der Punkte auf der konvexen Hülle.

Bitte beachten Sie, dass wir noch definieren müssen, was passieren soll, wenn drei Punkte auf der gleichen Linie liegen. Wenn man sich vorstellt, dass das Gummiband einen Punkt hat, an dem es einen der Nägel berührt, sich dort aber nicht krümmt, bedeutet das, dass der Nagel dort auf einer Geraden zwischen zwei anderen Nägeln liegt. Je nach Problemstellung könnte man diesen Nagel entlang der Geraden als Teil des Ausgangs betrachten, da er das Gummiband berührt. Andererseits könnte man auch sagen, dass dieser Nagel nicht zum Ergebnis gehört, weil sich die Form des Gummibandes nicht ändert, wenn man ihn entfernt. Diese Entscheidung hängt von dem Problem ab, an dem man gerade arbeitet, und am besten ist es, wenn man eine Eingabe hat, bei der keine drei Punkte kollinear sind (das ist bei einfachen Aufgaben für Programmierwettbewerbe oft der Fall), dann kann man dieses Problem sogar ganz ignorieren.

Finden der konvexen Hülle

Bei der Betrachtung einer Reihe von Punkten können wir mit menschlicher Intuition schnell herausfinden, welche Punkte wahrscheinlich die konvexe Hülle berühren und welche näher an der Mitte und damit von der konvexen Hülle entfernt sind. Um die konvexe Hülle eines Punktesatzes zu finden, können wir einen Algorithmus namens Graham Scan verwenden, der als einer der ersten Algorithmen der Computergeometrie gilt. Mit diesem Algorithmus können wir die Teilmenge der Punkte finden, die auf der konvexen Hülle liegen, zusammen mit der Reihenfolge, in der diese Punkte beim Umrunden der konvexen Hülle angetroffen werden.

Der Algorithmus beginnt mit der Suche nach einem Punkt, von dem wir wissen, dass er mit Sicherheit auf der konvexen Hülle liegt. Der Punkt mit der niedrigsten y-Koordinate kann zum Beispiel als sichere Wahl gelten. Gibt es mehrere Punkte an der gleichen y-Koordinate, wird derjenige genommen, der die größte x-Koordinate hat (das funktioniert auch mit anderen Eckpunkten, z.B. erst niedrigstes x dann niedrigstes y).

Als nächstes sortieren wir die anderen Punkte nach dem Winkel, in dem sie vom Startpunkt aus gesehen liegen. Wenn zwei Punkte zufällig im gleichen Winkel liegen, sollte der Punkt, der näher am Startpunkt liegt, in der Sortierung früher auftauchen.

Die Idee des Algorithmus ist es nun, um diese sortierte Anordnung herumzugehen und für jeden Punkt zu bestimmen, ob er auf der konvexen Hülle liegt oder nicht. Das bedeutet, dass wir für jede Dreiergruppe von Punkten, auf die wir treffen, entscheiden, ob sie eine konvexe oder eine konkave Ecke bilden. Wenn die Ecke konkav ist, dann wissen wir, dass der mittlere Punkt aus diesem Tripel nicht auf der konvexen Hülle liegen kann.

(Man beachte, dass die Begriffe konkave und konvexe Ecke in Bezug auf das gesamte Polygon verwendet werden müssen, nur eine Ecke allein kann nicht konvex oder konkav sein, da es keine Bezugsrichtung gibt.)

Wir speichern die Punkte, die auf der konvexen Hülle liegen, auf einem Stapel, so dass wir Punkte hinzufügen können, wenn wir sie auf unserem Weg durch die sortierten Punkte erreichen, und sie entfernen können, wenn wir feststellen, dass sie eine konkave Ecke bilden.

(Streng genommen müssen wir auf die beiden obersten Punkte des Stapels zugreifen, deshalb verwenden wir stattdessen ein std::vector, aber wir sehen es als eine Art Stapel an, weil wir uns immer nur um die obersten paar Elemente kümmern.)

Wenn wir um die sortierte Reihe von Punkten herumgehen, fügen wir den Punkt dem Stapel hinzu, und wenn wir später feststellen, dass der Punkt nicht zur konvexen Hülle gehört, entfernen wir ihn.

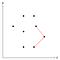
Wir können messen, ob die aktuelle Ecke nach innen oder nach außen gebogen ist, indem wir das Kreuzprodukt berechnen und prüfen, ob es positiv oder negativ ist. Die obige Abbildung zeigt eine Dreiergruppe von Punkten, deren Ecke konvex ist, daher bleibt der mittlere dieser drei Punkte vorerst auf dem Stapel.

Wenn wir zum nächsten Punkt übergehen, machen wir dasselbe: Wir prüfen, ob die Ecke konvex ist, und wenn nicht, entfernen wir den Punkt. Dann fügen wir den nächsten Punkt hinzu und wiederholen den Vorgang.

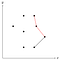
Diese rot markierte Ecke ist konkav, daher entfernen wir den mittleren Punkt vom Stapel, da er nicht Teil der konvexen Hülle sein kann.

Woher wissen wir, dass wir damit die richtige Antwort erhalten?

Einen strengen Beweis zu schreiben, würde den Rahmen dieses Artikels sprengen, aber ich kann die grundlegenden Ideen niederschreiben. Ich ermutige Sie jedoch, weiterzumachen und zu versuchen, die Lücken zu füllen!

Da wir das Kreuzprodukt an jeder Ecke berechnet haben, wissen wir mit Sicherheit, dass wir ein konvexes Polygon erhalten. Jetzt müssen wir nur noch beweisen, dass dieses konvexe Polygon wirklich alle Punkte einschließt.

(Eigentlich müsste man auch zeigen, dass dies das kleinstmögliche konvexe Polygon ist, das diese Bedingungen erfüllt, aber das folgt ganz einfach daraus, dass die Eckpunkte unseres konvexen Polygons eine Teilmenge der ursprünglichen Punktmenge sind.)

Angenommen, es gibt einen Punkt P außerhalb des soeben gefundenen Polygons.

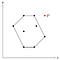
Da jeder Punkt einmal zum Stapel hinzugefügt wurde, wissen wir, dass P irgendwann vom Stapel entfernt wurde. Das bedeutet, dass P zusammen mit seinen Nachbarpunkten, nennen wir sie O und Q, eine konkave Ecke gebildet hat.

Da O und Q innerhalb des Polygons (oder an dessen Rand) liegen, müsste P auch innerhalb des Randes liegen, denn das Polygon ist konvex und die Ecke, die O und Q mit P bilden, ist in Bezug auf das Polygon konkav.

Damit haben wir einen Widerspruch gefunden, der bedeutet, dass es einen solchen Punkt P nicht geben kann.

Implementierung

Die hier bereitgestellte Implementierung hat eine Funktion convex_hull, die ein std::vector nimmt, das die Punkte als std::pairs von ints enthält und ein anderes std::vector zurückgibt, das die Punkte enthält, die auf der konvexen Hülle liegen.

Laufzeit- und Speicheranalyse

Es ist immer nützlich, über die Komplexität von Algorithmen in Form der Big-O-Notation nachzudenken, die ich hier nicht erläutern werde, weil Michael Olorunnisola sie bereits viel besser erklärt hat, als ich es wahrscheinlich tun würde:

Das Sortieren der Punkte benötigt anfangs O(n log n) Zeit, aber danach kann jeder Schritt in konstanter Zeit berechnet werden. Jeder Punkt wird höchstens einmal zum Stack hinzugefügt und wieder entfernt, d.h. die Worst-Case-Laufzeit liegt bei O(n log n).

Der Speicherverbrauch, der im Moment bei O(n) liegt, könnte optimiert werden, indem man den Stack überflüssig macht und die Operationen direkt auf dem Eingabe-Array durchführt. Wir könnten die Punkte, die auf der konvexen Hülle liegen, an den Anfang des Eingabe-Arrays verschieben und sie in der richtigen Reihenfolge anordnen, und die anderen Punkte würden in den Rest des Arrays verschoben werden. Die Funktion könnte dann nur eine einzige ganzzahlige Variable zurückgeben, die die Anzahl der Punkte im Array angibt, die auf der konvexen Hülle liegen. Dies hat natürlich den Nachteil, dass die Funktion sehr viel komplizierter wird. Ich würde daher davon abraten, es sei denn, Sie programmieren für eingebettete Systeme oder haben ähnlich restriktive Speicheranforderungen. In den meisten Situationen lohnt sich der Kompromiss zwischen Fehlerwahrscheinlichkeit und Speicherplatzersparnis einfach nicht.

Andere Algorithmen

Eine Alternative zum Graham Scan ist der Chan-Algorithmus, der im Grunde auf der gleichen Idee beruht, aber einfacher zu implementieren ist. Es ist jedoch sinnvoll, zuerst zu verstehen, wie der Graham Scan funktioniert.

Wenn Sie wirklich Lust haben und das Problem in drei Dimensionen angehen wollen, schauen Sie sich den Algorithmus von Preparata und Hong an, den sie 1977 in ihrer Arbeit „Convex Hulls of Finite Sets of Points in Two and Three Dimensions“ vorgestellt haben.