Eine kurze Einführung in den differenziellen Datenschutz
Aaruran Elamurugaiyan
Die Privatsphäre kann quantifiziert werden. Noch besser: Wir können eine Rangfolge der Strategien zur Wahrung der Privatsphäre aufstellen und sagen, welche davon effektiver ist. Noch besser: Wir können Strategien entwerfen, die selbst gegen Hacker, die über Zusatzinformationen verfügen, robust sind. Und als ob das nicht schon gut genug wäre, können wir all diese Dinge gleichzeitig tun. Diese und weitere Lösungen finden sich in einer probabilistischen Theorie, die als differentielle Privatsphäre bezeichnet wird.
Hier ist der Kontext. Wir pflegen (oder verwalten) eine sensible Datenbank und möchten einige Statistiken aus diesen Daten für die Öffentlichkeit freigeben. Wir müssen jedoch sicherstellen, dass es für einen Angreifer unmöglich ist, die sensiblen Daten aus den von uns freigegebenen Daten zurückzuentwickeln. Ein Angreifer ist in diesem Fall eine Partei, die die Absicht hat, zumindest einige unserer sensiblen Daten zu enthüllen oder zu erfahren. Differentieller Datenschutz kann Probleme lösen, die entstehen, wenn diese drei Zutaten – sensible Daten, Kuratoren, die Statistiken veröffentlichen müssen, und Gegner, die die sensiblen Daten zurückgewinnen wollen – vorhanden sind (siehe Abbildung 1). Dieses Reverse-Engineering ist eine Art der Verletzung der Privatsphäre.

Aber wie schwer ist es, die Privatsphäre zu verletzen? Würde es nicht ausreichen, die Daten zu anonymisieren? Wenn Sie Zusatzinformationen aus anderen Datenquellen haben, reicht die Anonymisierung nicht aus. Im Jahr 2007 veröffentlichte Netflix beispielsweise einen Datensatz mit Nutzerbewertungen als Teil eines Wettbewerbs, um zu sehen, ob jemand seinen Algorithmus für kollaborative Filterung übertreffen kann. Der Datensatz enthielt keine personenbezogenen Daten, aber die Forscher waren dennoch in der Lage, die Privatsphäre zu verletzen; sie konnten 99 % aller personenbezogenen Daten wiederherstellen, die aus dem Datensatz entfernt worden waren. In diesem Fall verletzten die Forscher die Privatsphäre mit Hilfe von Zusatzinformationen aus IMDB.
Wie kann man sich gegen einen Gegner verteidigen, der unbekannte und möglicherweise unbegrenzte Hilfe aus der Außenwelt hat? Differentielle Privatsphäre bietet eine Lösung. Differentiell-private Algorithmen sind resistent gegen adaptive Angriffe, die Hilfsinformationen verwenden. Diese Algorithmen beruhen auf der Einbeziehung von Zufallsrauschen in die Mischung, so dass alles, was ein Gegner erhält, verrauscht und ungenau wird und es somit viel schwieriger ist, die Privatsphäre zu verletzen (wenn es überhaupt möglich ist).
Rauschende Zählung
Lassen Sie uns ein einfaches Beispiel für das Einbringen von Rauschen betrachten. Nehmen wir an, wir verwalten eine Datenbank mit Kreditratings (zusammengefasst in Tabelle 1).
Für dieses Beispiel nehmen wir an, dass der Angreifer die Anzahl der Personen mit einer schlechten Kreditwürdigkeit wissen will (die 3 beträgt). Die Daten sind sensibel, so dass wir die Grundwahrheit nicht preisgeben können. Stattdessen werden wir einen Algorithmus verwenden, der die Grundwahrheit, N = 3, plus etwas Zufallsrauschen liefert. Dieser Grundgedanke (Hinzufügen von Zufallsrauschen zur Grundwahrheit) ist der Schlüssel zur differentiellen Privatsphäre. Nehmen wir an, wir wählen eine Zufallszahl L aus einer null-zentrierten Laplace-Verteilung mit einer Standardabweichung von 2 und erhalten N+L zurück. Wir werden die Wahl der Standardabweichung in ein paar Absätzen erklären. (Falls Sie noch nichts von der Laplace-Verteilung gehört haben, sehen Sie sich Abbildung 2 an). Wir werden diesen Algorithmus „verrauschtes Zählen“ nennen.
Was ist der Sinn dieses Algorithmus, wenn wir eine unsinnige, verrauschte Antwort geben? Die Antwort ist, dass er es uns ermöglicht, ein Gleichgewicht zwischen Nutzen und Privatsphäre herzustellen. Wir wollen, dass die Allgemeinheit einen gewissen Nutzen aus unserer Datenbank zieht, ohne einem möglichen Gegner sensible Daten preiszugeben.
Was würde der Gegner tatsächlich erhalten? Die Antworten sind in Tabelle 2 aufgeführt.

Die erste Antwort, die der Gegner erhält, ist nahe an der Grundwahrheit, aber nicht gleich. In diesem Sinne ist der Gegner getäuscht, der Nutzen ist gegeben, und die Privatsphäre ist geschützt. Aber nach mehreren Versuchen wird er in der Lage sein, die Grundwahrheit zu schätzen. Diese „Schätzung durch wiederholte Abfragen“ ist eine der grundlegenden Einschränkungen der differentiellen Privatsphäre. Wenn der Angreifer genügend Abfragen an eine differentiell-private Datenbank stellen kann, kann er die sensiblen Daten immer noch schätzen. Mit anderen Worten, mit immer mehr Abfragen wird die Privatsphäre verletzt. Tabelle 2 veranschaulicht diese Verletzung der Privatsphäre empirisch. Wie Sie jedoch sehen können, ist das 90 %-Konfidenzintervall bei diesen 5 Abfragen ziemlich breit; die Schätzung ist noch nicht sehr genau.
Wie genau kann diese Schätzung sein? Werfen Sie einen Blick auf Abbildung 3, wo wir eine Simulation mehrmals durchgeführt und die Ergebnisse aufgezeichnet haben.

Jede vertikale Linie zeigt die Breite eines 95 %-Konfidenzintervalls an, und die Punkte geben den Mittelwert der Daten des Gegners an. Man beachte, dass diese Diagramme eine logarithmische horizontale Achse haben und dass das Rauschen aus unabhängigen und identisch verteilten Laplace-Zufallsvariablen gezogen wird. Insgesamt wird der Mittelwert mit weniger Abfragen rauschiger (da die Stichprobengrößen klein sind). Wie erwartet werden die Konfidenzintervalle enger, wenn der Gegner mehr Abfragen macht (da der Stichprobenumfang zunimmt und das Rauschen im Durchschnitt gegen Null geht). Anhand des Diagramms können wir sehen, dass es etwa 50 Abfragen braucht, um eine vernünftige Schätzung zu machen.
Lassen Sie uns über dieses Beispiel nachdenken. In erster Linie haben wir es einem Angreifer durch das Hinzufügen von Zufallsrauschen erschwert, die Privatsphäre zu verletzen. Zweitens war die von uns angewandte Verschleierungsstrategie einfach zu implementieren und zu verstehen. Leider war der Angreifer mit immer mehr Abfragen in der Lage, sich der wahren Zahl anzunähern.
Wenn wir die Varianz des hinzugefügten Rauschens erhöhen, können wir unsere Daten besser schützen, aber wir können nicht einfach irgendein Laplace-Rauschen zu einer Funktion hinzufügen, die wir verbergen wollen. Der Grund dafür ist, dass die Menge des Rauschens, die wir hinzufügen müssen, von der Empfindlichkeit der Funktion abhängt, und jede Funktion hat ihre eigene Empfindlichkeit. Insbesondere die Zählfunktion hat eine Empfindlichkeit von 1. Sehen wir uns einmal an, was Empfindlichkeit in diesem Zusammenhang bedeutet.
Sensitivität und der Laplace-Mechanismus
Für eine Funktion:
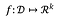
die Sensitivität von f ist:
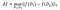
auf Datensätze D₁, D₂, die sich in höchstens einem Element unterscheiden.
Die obige Definition ist ziemlich mathematisch, aber sie ist nicht so schlecht, wie sie aussieht. Grob gesagt, ist die Sensitivität einer Funktion der größtmögliche Unterschied, den eine Zeile auf das Ergebnis dieser Funktion für einen beliebigen Datensatz haben kann. In unserem Spielzeugdatensatz hat die Zählung der Zeilen beispielsweise eine Empfindlichkeit von 1, da das Hinzufügen oder Entfernen einer einzigen Zeile aus einem Datensatz die Zählung um höchstens 1 verändert.
Als weiteres Beispiel nehmen wir an, dass „Zählung aufgerundet auf ein Vielfaches von 5“. Diese Funktion hat eine Empfindlichkeit von 5, und wir können dies ganz einfach zeigen. Wenn wir zwei Datensätze der Größe 10 und 11 haben, unterscheiden sie sich in einer Zeile, aber die „Zählungen aufgerundet auf ein Vielfaches von 5“ sind 10 bzw. 15. In der Tat ist fünf der größtmögliche Unterschied, den diese Beispielfunktion erzeugen kann. Daher ist ihre Empfindlichkeit 5.
Die Berechnung der Empfindlichkeit für eine beliebige Funktion ist schwierig. Ein beträchtlicher Teil der Forschungsanstrengungen gilt der Schätzung der Empfindlichkeit, der Verbesserung der Schätzungen der Empfindlichkeit und der Umgehung der Berechnung der Empfindlichkeit.
Wie hängt die Empfindlichkeit mit der verrauschten Zählung zusammen? Unsere Strategie der verrauschten Zählung verwendet einen Algorithmus, der Laplace-Mechanismus genannt wird und der wiederum auf der Empfindlichkeit der Funktion beruht, die er verdeckt. In Algorithmus 1 haben wir eine naive Pseudocode-Implementierung des Laplace-Mechanismus.
Algorithmus 1
Eingabe: Funktion F, Eingabe X, Geheimhaltungsgrad ϵ
Ausgabe: Eine verrauschte Antwort
Berechnen Sie F (X)
Berechnen Sie die Empfindlichkeit von F : S
Ziehen Sie das Rauschen L aus einer Laplace-Verteilung mit Varianz:
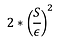
Rückgabe F(X) + L
Je größer die Empfindlichkeit S, desto verrauschter wird die Antwort sein. Das Zählen hat nur eine Empfindlichkeit von 1, so dass wir nicht viel Rauschen hinzufügen müssen, um die Privatsphäre zu bewahren.
Beachten Sie, dass der Laplace-Mechanismus in Algorithmus 1 einen Parameter epsilon benötigt. Wir werden diese Größe als den Verlust der Privatsphäre des Mechanismus bezeichnen und sie ist Teil der zentralen Definition auf dem Gebiet der differentiellen Privatsphäre: epsilon-differentielle Privatsphäre. Zur Veranschaulichung: Wenn wir uns an unser früheres Beispiel erinnern und etwas Algebra verwenden, können wir sehen, dass unser verrauschter Zählmechanismus epsilon-differentielle Privatsphäre hat, mit einem Epsilon von 0,707. Indem wir epsilon einstellen, kontrollieren wir die Verrauschtheit unserer verrauschten Zählung. Die Wahl eines kleineren epsilon führt zu verrauschten Ergebnissen und besseren Datenschutzgarantien. Als Referenz verwendet Apple ein epsilon von 2 in der differenziell-privaten Autokorrektur der Tastatur.
Die Größe epsilon ist die Art und Weise, wie differenzielle Privatsphäre strenge Vergleiche zwischen verschiedenen Strategien ermöglichen kann. Die formale Definition der epsilon-differentiellen Privatsphäre ist mathematisch etwas komplizierter, daher habe ich sie in diesem Blogbeitrag absichtlich weggelassen. Sie können mehr darüber in Dwork’s survey of differential privacy lesen.
Wie Sie sich erinnern, hatte das Beispiel des verrauschten Zählens ein Epsilon von 0,707, was ziemlich klein ist. Aber wir haben die Privatsphäre nach 50 Abfragen immer noch verletzt. Und warum? Weil mit zunehmender Anzahl von Abfragen das Budget für die Privatsphäre wächst und damit die Garantie für die Privatsphäre schlechter wird.
Das Budget für die Privatsphäre
Im Allgemeinen kumulieren die Verluste an Privatsphäre. Wenn zwei Antworten an einen Gegner zurückgegeben werden, ist der gesamte Verlust an Privatsphäre doppelt so groß, und die Garantie der Privatsphäre ist halb so stark. Diese kumulative Eigenschaft ist eine Folge des Kompositionstheorems. Im Wesentlichen werden mit jeder neuen Abfrage zusätzliche Informationen über die sensiblen Daten freigegeben. Das Kompositionstheorem ist daher pessimistisch und geht vom schlimmsten Fall aus: Bei jeder neuen Antwort wird die gleiche Menge an Informationen preisgegeben. Für starke Datenschutzgarantien soll der Verlust an Privatsphäre gering sein. In unserem Beispiel, in dem wir einen Verlust der Privatsphäre von fünfunddreißig (nach 50 Abfragen an unseren verrauschten Laplace-Zählmechanismus) haben, ist die entsprechende Datenschutzgarantie schwach.
Wie funktioniert der differenzierte Datenschutz, wenn der Verlust der Privatsphäre so schnell wächst? Um eine sinnvolle Datenschutzgarantie zu gewährleisten, können Datenverwalter einen maximalen Datenschutzverlust durchsetzen. Übersteigt die Anzahl der Abfragen den Schwellenwert, wird die Datenschutzgarantie zu schwach und der Datenverwalter stellt die Beantwortung der Abfragen ein. Der maximale Datenschutzverlust wird als Datenschutzbudget bezeichnet. Wir können uns jede Anfrage als eine „Ausgabe“ für die Privatsphäre vorstellen, die einen inkrementellen Verlust an Privatsphäre verursacht. Die Strategie der Verwendung von Budgets, Ausgaben und Verlusten wird passenderweise als Privacy Accounting bezeichnet.
Privacy Accounting ist eine effektive Strategie zur Berechnung des Verlusts an Privatsphäre nach mehreren Abfragen, aber sie kann immer noch das Kompositionstheorem berücksichtigen. Wie bereits erwähnt, geht das Kompositionstheorem vom schlimmsten Fall aus. Mit anderen Worten, es gibt bessere Alternativen.
Deep Learning
Deep Learning ist ein Teilgebiet des maschinellen Lernens, das sich mit dem Training von tiefen neuronalen Netzen (DNNs) zur Schätzung unbekannter Funktionen befasst. (Auf einer höheren Ebene ist ein DNN eine Folge von affinen und nichtlinearen Transformationen, die einen n-dimensionalen Raum auf einen m-dimensionalen Raum abbilden.) Ihre Anwendungen sind weit verbreitet und müssen hier nicht wiederholt werden. Wir werden untersuchen, wie man ein tiefes neuronales Netz privat trainiert.
Tiefe neuronale Netze werden normalerweise mit einer Variante des stochastischen Gradientenabstiegs (SGD) trainiert. Abadi et al. haben eine datenschutzfreundliche Version dieses beliebten Algorithmus entwickelt, die gemeinhin als „private SGD“ (oder PSGD) bezeichnet wird. Abbildung 4 veranschaulicht die Leistungsfähigkeit ihrer neuen Technik. Abadi et al. haben einen neuen Ansatz entwickelt: den Momentenbuchhalter. Die Grundidee des Momentenbuchhalters besteht darin, die Ausgaben für den Schutz der Privatsphäre zu akkumulieren, indem der Verlust der Privatsphäre als Zufallsvariable dargestellt wird und seine momentgenerierenden Funktionen verwendet werden, um die Verteilung dieser Variablen besser zu verstehen (daher der Name). Die vollständigen technischen Details liegen außerhalb des Rahmens eines einführenden Blog-Beitrags, aber wir ermutigen Sie, die Originalarbeit zu lesen, um mehr zu erfahren.

Abschließende Überlegungen
Wir haben die Theorie der differentiellen Privatsphäre besprochen und gesehen, wie sie zur Quantifizierung der Privatsphäre verwendet werden kann. Die Beispiele in diesem Beitrag zeigen, wie die grundlegenden Ideen angewandt werden können und welche Verbindung zwischen Anwendung und Theorie besteht. Es ist wichtig, daran zu denken, dass sich die Datenschutzgarantien bei wiederholter Nutzung verschlechtern. Es lohnt sich also, darüber nachzudenken, wie man dies abmildern kann, sei es durch Datenschutzbudgetierung oder andere Strategien. Sie können die Verschlechterung untersuchen, indem Sie auf diesen Satz klicken und unsere Experimente wiederholen. Es gibt noch viele Fragen, die hier nicht beantwortet wurden, und eine Fülle von Literatur, die es zu erforschen gilt – siehe die Referenzen unten. Wir ermutigen Sie, weiter zu lesen.
Cynthia Dwork. Differential Privacy: A survey of results. International Conference on Theory and Applications of Models of Computation, 2008.
Wikipedia Contributors. Laplace distribution, Juli 2018.
Aaruran Elamurugaiyan. Plots demonstrating standard error of differentially private responses over number of queries, August 2018.
Benjamin I. P. Rubinstein and Francesco Alda. Pain-free random differential privacy with sensitivity sampling. In 34th International Conference on Machine Learning (ICML’2017) , 2017.
Cynthia Dwork and Aaron Roth. The algorithmic foundations of differential privacy . Now Publ., 2014.
Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan Mcmahan, Ilya Mironov, Kunal Talwar, and Li Zhang. Deep Learning mit differenzieller Privatsphäre. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security – CCS16 , 2016.
Frank D. McSherry. Privacy integrated queries: Eine erweiterbare Plattform zur datenschutzfreundlichen Datenanalyse. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data , SIGMOD ’09, pages 19-30, New York, NY, USA, 2009. ACM.
Wikipedia Contributors. Deep Learning, August 2018.
Leave a Reply