Differentialgleichungen – Eigenwerte und Eigenfunktionen
Mobilen Hinweis anzeigen Alle Notizen anzeigen Alle Notizen ausblenden
Abschnitt 8-2: Eigenwerte und Eigenfunktionen
Wie im vorigen Abschnitt müssen wir erneut darauf hinweisen, dass wir nur einen kurzen Blick auf das Thema Eigenwerte und Eigenfunktionen für Randwertprobleme werfen werden. Es gibt eine ganze Reihe von Ideen, auf die wir hier nicht eingehen werden. Die Absicht dieses Abschnitts ist einfach, Ihnen eine Vorstellung von dem Thema zu geben und genug Arbeit zu leisten, um uns die Lösung einiger grundlegender partieller Differentialgleichungen im nächsten Kapitel zu ermöglichen.
Bevor wir nun über das eigentliche Thema dieses Abschnitts sprechen, lassen Sie uns ein Thema aus der Linearen Algebra in Erinnerung rufen, das wir zuvor in diesen Notizen kurz besprochen haben. Wenn wir für eine gegebene quadratische Matrix, \(A\), Werte von \(\lambda \) finden konnten, für die wir Lösungen ungleich Null finden konnten, d.h. \(\vec x \ne \vec 0\), zu,
\
dann nannten wir \(\lambda \) einen Eigenwert von \(A\) und \(\vec x\) war sein entsprechender Eigenvektor.
Es ist wichtig, sich daran zu erinnern, dass wir, damit \(\lambda \) ein Eigenwert sein kann, in der Lage sein müssen, Lösungen ungleich Null für die Gleichung zu finden.
Was hat das nun mit Randwertproblemen zu tun? Nun, gehen Sie zurück zum vorherigen Abschnitt und schauen Sie sich Beispiel 7 und Beispiel 8 an. In diesen beiden Beispielen haben wir homogene (und das ist wichtig!) BVP’s in der Form,
\
In Beispiel 7 hatten wir \(\lambda = 4\) und wir fanden nicht-triviale (d.h. ungleich Null) Lösungen für das BVP. In Beispiel 8 haben wir \(\lambda = 3\) verwendet und die einzige Lösung war die triviale Lösung (d. h. \(y\left( t \right) = 0\)). Diese homogene BVP (zur Erinnerung: das bedeutet auch, dass die Randbedingungen Null sind) scheint also ein ähnliches Verhalten wie die obige Matrixgleichung zu zeigen. Es gibt Werte von \(\lambda \), die nicht-triviale Lösungen für dieses BVP ergeben, und Werte von \(\lambda \), die nur die triviale Lösung zulassen.
Für die Werte von \(\lambda \), die nicht-triviale Lösungen ergeben, nennen wir \(\lambda \) einen Eigenwert für das BVP und die nicht-trivialen Lösungen werden Eigenfunktionen für das BVP genannt, die dem gegebenen Eigenwert entsprechen.
Wir wissen nun, dass für das in \(\eqref{eq:eq1}\) gegebene homogene BVP \(\lambda = 4\) ein Eigenwert ist (mit Eigenfunktionen \(y\left( x \right) = {c_2}\sin \left( {2x} \right)\)) und dass \(\lambda = 3\) kein Eigenwert ist.
Schließlich werden wir versuchen zu bestimmen, ob es noch andere Eigenwerte für \(\eqref{eq:eq1}\) gibt, aber bevor wir das tun, lassen Sie uns kurz darauf eingehen, warum es in dieser Diskussion so wichtig ist, dass das BVP homogen ist. In Beispiel 2 und Beispiel 3 des vorigen Abschnitts haben wir die homogene Differentialgleichung
\
mit zwei verschiedenen inhomogenen Randbedingungen in der Form,
\
gelöst. In diesen beiden Beispielen haben wir gesehen, dass wir durch einfaches Ändern des Wertes von \(a\) und/oder \(b\) entweder nichttriviale Lösungen erhalten oder überhaupt keine Lösung erzwingen konnten. Bei der Diskussion von Eigenwerten/Eigenfunktionen müssen Lösungen existieren, und die einzige Möglichkeit, dieses Verhalten zu gewährleisten, besteht darin, dass die Randbedingungen ebenfalls homogen sein müssen. Mit anderen Worten, das BVP muss homogen sein.
Es gibt noch ein letztes Thema, das wir besprechen müssen, bevor wir uns dem Thema Eigenwerte und Eigenfunktionen zuwenden, und das ist eher eine Frage der Notation, die uns bei der Arbeit helfen wird, die wir tun müssen.
Angenommen, wir haben eine Differentialgleichung zweiter Ordnung und ihr charakteristisches Polynom hat zwei reelle, eindeutige Wurzeln, und sie haben die Form
\
Dann wissen wir, dass die Lösung ist,
\
Während es an dieser Lösung nichts auszusetzen gibt, wollen wir sie ein wenig umschreiben. Wir beginnen damit, die Terme wie folgt aufzuteilen,
\
Nun addieren/subtrahieren wir die folgenden Terme (beachten Sie, dass wir \({c_i}\) und \( \pm \,\alpha \) in den neuen Termen „mischen“), um zu erhalten,
\
Als Nächstes ordnen wir die Terme ein wenig um,
\
Schließlich faktorisieren wir die Mengen in Klammern und verschieben auch den Ort des Bruches. Auf diese Weise und durch die Umbenennung der neuen Konstanten erhalten wir,
\
Diese ganze Arbeit erscheint wahrscheinlich sehr mysteriös und unnötig. Es gab jedoch wirklich einen Grund dafür. In der Tat haben Sie den Grund vielleicht schon gesehen, zumindest zum Teil. Die beiden „neuen“ Funktionen, die wir in unserer Lösung haben, sind in Wirklichkeit zwei der hyperbolischen Funktionen. Insbesondere,
\
Eine andere Art, die Lösung einer Differentialgleichung zweiter Ordnung zu schreiben, deren charakteristisches Polynom zwei reelle, eindeutige Wurzeln in der Form \({r_1} = \alpha ,\,\,{r_2} = – \,\alpha \) hat, ist,
\
Die Lösung in dieser Form für einige (eigentlich die meisten) der von uns zu untersuchenden Probleme zu haben, wird unser Leben sehr viel einfacher machen. Die hyperbolischen Funktionen haben einige sehr nette Eigenschaften, die wir uns zunutze machen können (und werden).
Erstens, da wir sie später brauchen werden, sind die Ableitungen,
\
Nächstens wollen wir einen kurzen Blick auf die Graphen dieser Funktionen werfen.
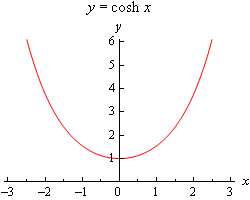

Beachte, dass \(\cosh \left( 0 \right) = 1\) und \(\sinh \left( 0 \right) = 0\). Da wir oft mit Randbedingungen bei \(x = 0\) arbeiten werden, sind dies nützliche Auswertungen.
Als Nächstes, und vielleicht noch wichtiger, stellen wir fest, dass \(\cosh \left( x \right) > 0\) für alle \(x\) und somit der hyperbolische Kosinus niemals Null sein wird. Gleichermaßen können wir sehen, dass \(\sinh \left( x \right) = 0\) nur dann gilt, wenn \(x = 0\). Wir werden diese beiden Tatsachen in einigen unserer Arbeiten verwenden, also sollten wir sie nicht vergessen.
Okay, jetzt, wo wir das alles hinter uns haben, lasst uns an einem Beispiel arbeiten, um zu sehen, wie wir Eigenwerte/Eigenfunktionen für ein BVP finden.
Wir haben diesen Abschnitt damit begonnen, dieses BVP zu betrachten, und wir kennen bereits einen Eigenwert (\(\lambda = 4\)) und wir kennen einen Wert von \(\lambda \), der kein Eigenwert ist (\(\lambda = 3\)). Während wir hier arbeiten, müssen wir uns daran erinnern, dass wir einen Eigenwert für einen bestimmten Wert von \(\lambda \) erhalten, wenn wir nicht-triviale Lösungen des BVP für diesen bestimmten Wert von \(\lambda \) erhalten.
Um zu wissen, dass wir alle Eigenwerte gefunden haben, können wir nicht einfach anfangen, zufällig Werte von \(\lambda \) auszuprobieren, um zu sehen, ob wir nicht-triviale Lösungen erhalten oder nicht. Glücklicherweise gibt es einen Weg, dies zu tun, der nicht allzu schlimm ist und uns alle Eigenwerte/Eigenfunktionen liefern wird. Wir müssen jedoch einige Fälle lösen. Die drei Fälle, die wir uns ansehen müssen, sind: \(\lambda > 0\), \(\lambda = 0\), und \(\lambda < 0\). Jeder dieser Fälle ergibt eine spezifische Form der Lösung des BVP, auf die wir dann die Randbedingungen anwenden können, um zu sehen, ob wir nicht-triviale Lösungen erhalten oder nicht. Fangen wir also mit den Fällen an.
\(\underline {\lambda > 0} \)
In diesem Fall ist das charakteristische Polynom, das wir aus der Differentialgleichung erhalten,
\
In diesem Fall, da wir wissen, dass \(\lambda > 0\) diese Wurzeln komplex sind, können wir sie stattdessen schreiben als,
\
Die allgemeine Lösung der Differentialgleichung ist dann,
\
Wenn wir die erste Randbedingung anwenden, erhalten wir,
\
Wenn wir dies berücksichtigen und die zweite Randbedingung anwenden, erhalten wir,
\
Das bedeutet, dass wir eine der folgenden Möglichkeiten haben müssen,
\
Erinnern wir uns jedoch daran, dass wir nicht-triviale Lösungen wollen, und wenn wir die erste Möglichkeit haben, erhalten wir die triviale Lösung für alle Werte von \(\lambda > 0\). Nehmen wir also an, dass \({c_2} \ne 0\). Das bedeutet, dass wir,
\
Mit anderen Worten, wenn wir die Tatsache nutzen, dass wir wissen, wo der Sinus Null ist, können wir die zweite Gleichung aufstellen. Da wir davon ausgehen, dass \(\lambda > 0\) ist, wissen wir auch, dass \(2\pi \sqrt \lambda > 0\) und somit kann \(n\) in diesem Fall nur eine positive ganze Zahl sein.
Jetzt müssen wir das nur noch für \(\lambda \) lösen und wir haben alle positiven Eigenwerte für dieses BVP.
Die positiven Eigenwerte sind dann,
\
und die Eigenfunktionen, die diesen Eigenwerten entsprechen, sind,
\
Beachten Sie, dass wir ein \(n\) an die Eigenwerte und Eigenfunktionen angehängt haben, um die Tatsache zu kennzeichnen, dass es für jeden der gegebenen Werte von \(n\) einen gibt. Beachten Sie auch, dass wir das \({c_2}\) bei den Eigenfunktionen weggelassen haben. Bei Eigenfunktionen sind wir nur an der Funktion selbst interessiert und nicht an der Konstante, die ihr vorangestellt ist, und deshalb lassen wir sie im Allgemeinen weg.
Wenden wir uns nun dem zweiten Fall zu.
\(\underline {\lambda = 0} \)
In diesem Fall wird die BVP,
\
und die Integration der Differentialgleichung ein paar Mal gibt uns die allgemeine Lösung,
\
Die Anwendung der ersten Randbedingung ergibt,
\
Wendet man die zweite Randbedingung sowie die Ergebnisse der ersten Randbedingung an, so erhält man,
\
Hier haben wir im Gegensatz zum ersten Fall keine Wahl, wie wir diesen Wert auf Null bringen. Er wird nur dann Null, wenn \({c_2} = 0\).
Daher ist für dieses BVP (und das ist wichtig), wenn wir \(\lambda = 0\) haben, die einzige Lösung die triviale Lösung und somit kann \(\lambda = 0\) kein Eigenwert für dieses BVP sein.
Betrachten wir nun den letzten Fall.
\(\underline {\lambda < 0} \)
In diesem Fall sind die charakteristische Gleichung und ihre Wurzeln dieselben wie im ersten Fall. Wir wissen also, dass,
\
Da wir hier jedoch von \(\lambda < 0\) ausgehen, handelt es sich nun um zwei reale, eindeutige Wurzeln, und wenn wir unsere obige Arbeit für diese Art von realen, eindeutigen Wurzeln verwenden, wissen wir, dass die allgemeine Lösung sein wird,
\
Beachten Sie, dass wir hier die exponentielle Form der Lösung hätten verwenden können, aber unsere Arbeit wird wesentlich einfacher sein, wenn wir hier die hyperbolische Form der Lösung verwenden.
Nun ergibt die Anwendung der ersten Randbedingung,
\
Die Anwendung der zweiten Randbedingung ergibt,
\
Da wir von \(\lambda < 0\) ausgehen, wissen wir, dass \(2\pi \sqrt { – \lambda } \ne 0\) und somit wissen wir auch, dass \(\sinh \left( {2\pi \sqrt { – \lambda } } \right) \ne 0\). Daher müssen wir, ähnlich wie im zweiten Fall, \({c_2} = 0\) haben.
Wenn wir also für dieses BVP (auch das ist wichtig) \(\lambda < 0\) haben, erhalten wir nur die triviale Lösung und es gibt keine negativen Eigenwerte.
Zusammengefasst haben wir dann die folgenden Eigenwerte/Eigenfunktionen für dieses BVP.
\
Schauen wir uns ein anderes Beispiel mit etwas anderen Randbedingungen an.
Hier werden wir mit abgeleiteten Randbedingungen arbeiten. Die Arbeit ist jedoch ziemlich identisch mit dem vorherigen Beispiel, so dass wir hier nicht ganz so detailliert vorgehen werden. Wir müssen alle drei Fälle durchgehen, genau wie im vorherigen Beispiel, also fangen wir damit an.
(\underline {\lambda > 0} \)
Die allgemeine Lösung der Differentialgleichung ist identisch mit dem vorherigen Beispiel und wir haben also,
\
Wenn man die erste Randbedingung anwendet, erhält man,
\
Erinnern Sie sich daran, dass wir davon ausgehen, dass \(\lambda > 0\) hier nur Null ist, wenn \({c_2} = 0\). Nun, die zweite Randbedingung gibt uns,
\
Erinnern Sie sich, dass wir keine trivialen Lösungen wollen und dass \(\lambda > 0\), so dass wir nur eine nicht-triviale Lösung erhalten, wenn wir verlangen, dass,
\
Auflösen für \(\lambda \) und wir sehen, dass wir genau die gleichen positiven Eigenwerte für dieses BVP erhalten, die wir im vorherigen Beispiel erhalten haben.
\
Die Eigenfunktionen, die diesen Eigenwerten entsprechen, sind jedoch,
\
So erhalten wir für dieses BVP Kosinus für Eigenfunktionen, die positiven Eigenwerten entsprechen.
Nun der zweite Fall.
\(\underline {\lambda = 0} \)
Die allgemeine Lösung ist,
\
Die Anwendung der ersten Randbedingung ergibt,
\
Damit ist die allgemeine Lösung dann,
\
und man beachte, dass diese trivialerweise die zweite Randbedingung erfüllen wird,
\
Daher ist, anders als im ersten Beispiel, \(\lambda = 0\) ein Eigenwert für dieses BVP und die diesem Eigenwert entsprechende Eigenfunktion ist,
\
Auch hier ist zu beachten, dass wir die beliebige Konstante für die Eigenfunktionen weggelassen haben.
Schließlich kümmern wir uns um den dritten Fall.
\(\underline {\lambda < 0} \)
Die allgemeine Lösung ist hier,
\
Anwendung der ersten Randbedingung ergibt,
\
Anwendung der zweiten Randbedingung ergibt,
\
Wie beim vorherigen Beispiel wissen wir wieder, dass \(2\pi \sqrt { – \lambda } \ne 0\) und somit \(\sinh \left( {2\pi \sqrt { – \lambda } } \right) \ne 0\). Daher müssen wir \({c_1} = 0\) haben.
So haben wir für dieses BVP wieder keine negativen Eigenwerte.
Zusammenfassend haben wir dann die folgenden Eigenwerte/Eigenfunktionen für dieses BVP.
\
Beachten Sie auch, dass wir diese tatsächlich kombinieren können, wenn wir zulassen, dass die Liste der \(n\)’s für das erste bei Null statt bei Eins beginnt. Das wird nicht oft vorkommen, aber wenn es passiert, werden wir es ausnutzen. Die „offizielle“ Liste der Eigenwerte/Eigenfunktionen für dieses BVP lautet also:
\
In den beiden vorangegangenen Beispielen haben wir also gesehen, dass wir im Allgemeinen verschiedene Fälle für \(\lambda \) in Betracht ziehen müssen, da unterschiedliche Werte oft zu unterschiedlichen allgemeinen Lösungen führen. Man sollte sich nicht zu sehr auf die Fälle versteifen, die wir hier betrachtet haben. Wir werden meistens diese spezielle Differentialgleichung lösen und daher ist es verlockend anzunehmen, dass dies immer die Fälle sind, die wir betrachten werden, aber es gibt BVPs, die andere/andere Fälle erfordern.
Auch, wie wir in den beiden Beispielen gesehen haben, werden manchmal einer oder mehrere der Fälle keine Eigenwerte liefern. Das kommt oft vor, aber auch hier sollten wir nichts in die Tatsache hineininterpretieren, dass wir für diese beiden BVP’s keine negativen Eigenwerte hatten. Es gibt BVP’s, die negative Eigenwerte haben.
Werfen wir einen Blick auf ein anderes Beispiel mit ganz anderen Randbedingungen. Dies sind nicht die traditionellen Randbedingungen, die wir bisher betrachtet haben, aber wir werden im nächsten Kapitel sehen, wie diese bei bestimmten physikalischen Problemen auftreten können.
In diesem Beispiel werden wir also nicht die Lösung oder ihre Ableitung an den Grenzen angeben. Stattdessen geben wir einfach an, dass die Lösung an den beiden Rändern gleich sein muss und die Ableitung der Lösung an den beiden Rändern ebenfalls gleich sein muss. Außerdem wird diese Art von Randbedingung typischerweise auf einem Intervall der Form liegen, statt wie bisher auf einem Intervall.
Wie oben erwähnt, treten diese Art von Randbedingungen ganz natürlich in bestimmten physikalischen Problemen auf, und wir werden das im nächsten Kapitel sehen.
Wie bei den beiden vorherigen Beispielen haben wir noch die drei Standardfälle zu betrachten.
\(\underline {\lambda > 0} \)
Die allgemeine Lösung für diesen Fall ist,
\
Anwendung der ersten Randbedingung und Nutzung der Tatsache, dass der Kosinus eine gerade Funktion ist (d.h.\(\cos \left( { – x} \right) = \cos \left( x \right)\)) und dass Sinus eine ungerade Funktion ist (d.h. \(\sin \left( { – x} \right) = – \sin \left( x \right)\)). ergibt,
\
Im Gegensatz zu den beiden vorangegangenen Beispielen sagt uns das dieses Mal nicht wirklich etwas. Wir könnten \(\sin \left( {\pi \sqrt \lambda } \right) = 0\) haben, aber es ist auch völlig möglich, an diesem Punkt des Problems sowieso, dass wir auch \({c_2} = 0\) haben.
Wenden wir also die zweite Randbedingung an und sehen wir, ob wir etwas dabei herausbekommen.
\
So erhalten wir etwas sehr Ähnliches wie nach der Anwendung der ersten Randbedingung. Da wir davon ausgehen, dass \(\lambda > 0\) dies sagt uns, dass entweder \(\sin \left( {\pi \sqrt \lambda } \right) = 0\) oder \({c_1} = 0\).
Beachte jedoch, dass wenn \(\sin \left( {\pi \sqrt \lambda } \right) \ne 0\) dann müssen wir \({c_1} = {c_2} = 0\) haben und wir erhalten die triviale Lösung. Wir müssen also voraussetzen, dass \(\sin \left( {\pi \sqrt \lambda } \right) = 0\) und so, wie wir es für die beiden vorherigen Beispiele getan haben, können wir jetzt die Eigenwerte erhalten,
\
Wenn wir uns daran erinnern, dass \(\lambda > 0\) ist, können wir sehen, dass wir die Liste der möglichen \(n\)’s bei 1 statt bei 0 beginnen müssen.
So, wir kennen jetzt die Eigenwerte für diesen Fall, aber was ist mit den Eigenfunktionen. Die Lösung für einen gegebenen Eigenwert ist,
\
und wir haben keinen Grund zu glauben, dass eine der beiden Konstanten null oder ungleich null ist. In Fällen wie diesen erhalten wir zwei Sätze von Eigenfunktionen, eine für jede Konstante. Die beiden Sätze von Eigenfunktionen für diesen Fall lauten:
\
Nun der zweite Fall.
\(\underline {\lambda = 0} \)
Die allgemeine Lösung ist,
\
Wenn man die erste Randbedingung anwendet, erhält man,
\
Die allgemeine Lösung ist dann,
\
und man beachte, dass dies trivialerweise die zweite Randbedingung erfüllt, genau wie wir im zweiten Beispiel oben gesehen haben. Daher haben wir wieder \(\lambda = 0\) als Eigenwert für dieses BVP und die diesem Eigenwert entsprechende Eigenfunktion ist,
\
Schließlich wollen wir uns um den dritten Fall kümmern.
\(\underline {\lambda < 0} \)
Die allgemeine Lösung ist hier,
\
Die Anwendung der ersten Randbedingung und die Tatsache, dass der hyperbolische Kosinus gerade und der hyperbolische Sinus ungerade ist, ergibt,
\
Nun gehen wir in diesem Fall davon aus, dass \(\lambda < 0\) und somit wissen wir, dass \(\pi \sqrt { – \lambda } \ne 0\) was uns wiederum sagt, dass \(\sinh \left( {\pi \sqrt { – \lambda } } \right) \ne 0\). Wir müssen also \({c_2} = 0\) haben.
Wenden wir nun die zweite Randbedingung an, um zu erhalten,
\
Durch unsere Annahme zu \(\lambda \) haben wir auch hier keine andere Wahl, als \({c_1} = 0\) zu haben.
Daher ist in diesem Fall die einzige Lösung die Triviallösung und somit haben wir für dieses BVP wieder keine negativen Eigenwerte.
Zusammenfassend haben wir dann folgende Eigenwerte/Eigenfunktionen für dieses BVP.
\
Beachten Sie, dass wir für \(\lambda > 0\) zwei Sätze von Eigenfunktionen hatten, indem wir sie jeweils separat aufgeführt haben. Außerdem können wir die letzten beiden wieder zu einem Satz von Eigenwerten und Eigenfunktionen zusammenfassen. Auf diese Weise erhalten wir den folgenden Satz von Eigenwerten und Eigenfunktionen.
\
Wieder einmal haben wir ein Beispiel ohne negative Eigenwerte. Wir können nicht genug betonen, dass dies mehr eine Funktion der Differentialgleichung ist, mit der wir arbeiten, als alles andere, und es wird Beispiele geben, in denen wir negative Eigenwerte erhalten können.
Nun haben wir bis zu diesem Punkt nur mit einer Differentialgleichung gearbeitet, also lassen Sie uns ein Beispiel mit einer anderen Differentialgleichung bearbeiten, um sicherzustellen, dass wir nicht zu sehr auf diese eine Differentialgleichung fixiert sind.
Bevor wir dieses Beispiel bearbeiten, lassen Sie uns anmerken, dass wir immer noch die große Mehrheit unserer Beispiele mit der einen Differentialgleichung bearbeiten werden, die wir bis zu diesem Punkt verwendet haben. Wir arbeiten mit dieser anderen Differentialgleichung, um sicherzustellen, dass wir uns nicht zu sehr auf eine einzige Differentialgleichung festlegen.
Dies ist eine Eulersche Differentialgleichung und wir wissen, dass wir die Wurzeln der folgenden Quadratischen finden müssen.
\
Die Wurzeln dieser Quadratischen sind,
\
Nun haben wir wieder einige Fälle, mit denen wir arbeiten müssen, aber sie sind nicht dieselben wie die vorherigen Beispiele. Die Lösung hängt davon ab, ob die Wurzeln reell, doppelt oder komplex sind, und diese Fälle hängen vom Vorzeichen/Wert von \(1 – \lambda \) ab. Gehen wir also die Fälle durch.
\(\underline {1 – \lambda < 0,\,\,\lambda > 1} \)
In diesem Fall sind die Wurzeln komplex und wir müssen sie wie folgt schreiben, um die Lösung aufzuschreiben.
\
Indem wir die Wurzeln auf diese Weise schreiben, wissen wir, dass \(\lambda – 1 > 0\) und somit \(\sqrt {\lambda – 1} \) nun eine reelle Zahl ist, die wir benötigen, um die folgende Lösung zu schreiben,
\
Die Anwendung der ersten Randbedingung liefert uns,
\
Die zweite Randbedingung ergibt,
\
Um die triviale Lösung für diesen Fall zu vermeiden, benötigen wir,
\
Dies ist eine viel kompliziertere Bedingung als die, die wir bisher gesehen haben, aber ansonsten machen wir das Gleiche. Die Lösung von \(\lambda \) liefert uns also die folgende Reihe von Eigenwerten für diesen Fall.
\
Beachten Sie, dass wir die Liste von \(n\) bei eins und nicht bei null beginnen müssen, um sicherzustellen, dass wir \(\lambda > 1\) haben, wie wir es für diesen Fall annehmen.
Die Eigenfunktionen, die diesen Eigenwerten entsprechen, sind,
\
Nun der zweite Fall.
\(\underline {1 – \lambda = 0,\,\,\,\lambda = 1} \)
In diesem Fall erhalten wir eine Doppelwurzel aus \({r_{\,1,2}} = – 1\) und somit ist die Lösung,
\
Anwendung der ersten Randbedingung ergibt,
\
Die zweite Randbedingung ergibt,
\
Wir haben also nur die triviale Lösung für diesen Fall und somit ist,
\(\lambda = 1\) kein Eigenwert.
Kümmern wir uns nun um den dritten (und letzten) Fall.
\(\underline {1 – \lambda > 0,\,\,\lambda < 1} \)
Dieser Fall hat zwei verschiedene reelle Wurzeln und die Lösung ist,
\
Die Anwendung der ersten Randbedingung ergibt,
\
Damit wird unsere Lösung,
\
Wenn man die zweite Randbedingung anwendet, erhält man,
\
Nun, da wir wissen, dass \(\lambda \ne 1\) für diesen Fall die Exponenten der beiden Terme in der Klammer nicht gleich sind, ist der Term in der Klammer nicht die Null. Das bedeutet, dass wir nur,
\
haben können und somit haben wir in diesem Fall nur die Triviallösung und es gibt keine Eigenwerte, für die \(\lambda < 1\).
Die einzigen Eigenwerte für diese BVP stammen dann aus dem ersten Fall.
So, wir haben jetzt ein Beispiel mit einer anderen Differentialgleichung als der „Standard“-Gleichung, die wir bis hierher verwendet haben, bearbeitet. Wie wir in der Arbeit gesehen haben, war der grundlegende Prozess jedoch ziemlich gleich. Wir haben festgestellt, dass es eine Reihe von Fällen gibt (hier drei, aber es werden nicht immer drei sein), die unterschiedliche Lösungen ergeben. Wir untersuchten jeden Fall, um festzustellen, ob nicht-triviale Lösungen möglich waren, und wenn ja, fanden wir die Eigenwerte und Eigenfunktionen, die diesem Fall entsprachen.
Wir müssen in diesem Abschnitt ein letztes Beispiel bearbeiten, bevor wir uns neuen Themen zuwenden. Die vier Beispiele, die wir bis zu diesem Punkt bearbeitet haben, waren alle ziemlich einfach (wobei einfach natürlich relativ ist…), aber wir wollen nicht gehen, ohne anzuerkennen, dass viele Eigenwert-/Eigenfunktionsprobleme so einfach sind.
In vielen Beispielen ist es nicht einmal möglich, eine vollständige Liste aller möglichen Eigenwerte für ein BVP zu erhalten. Oft sind die Gleichungen, die wir lösen müssen, um die Eigenwerte zu erhalten, schwer oder gar nicht exakt zu lösen. Schauen wir uns also ein Beispiel wie dieses an, um zu sehen, was man tun kann, um zumindest eine Vorstellung davon zu bekommen, wie die Eigenwerte in solchen Fällen aussehen.
Die Randbedingungen für dieses BVP unterscheiden sich ziemlich von denen, mit denen wir bisher gearbeitet haben. Der grundlegende Prozess ist jedoch derselbe. Fangen wir also mit dem ersten Fall an.
\(\underline {\lambda > 0} \)
Die allgemeine Lösung der Differentialgleichung ist identisch mit den ersten Beispielen und so haben wir,
\
Die Anwendung der ersten Randbedingung gibt uns,
\
Die zweite Randbedingung gibt uns,
\
So, wenn wir \({c_2} = 0\) lassen, erhalten wir die triviale Lösung, und um diese Randbedingung zu erfüllen, müssen wir stattdessen fordern,
\
Nun hat diese Gleichung Lösungen, aber wir müssen einige numerische Techniken anwenden, um sie zu erhalten. Um zu sehen, was hier vor sich geht, stellen wir \(\tan \left( {\sqrt \lambda } \right)\) und \( – \sqrt \lambda \) auf demselben Graphen dar. Hier ist dieses Diagramm und man beachte, dass die horizontale Achse wirklich die Werte von \(\sqrt \lambda \) ist, da dies die Dinge ein wenig einfacher zu sehen macht und sich auf Werte bezieht, mit denen wir vertraut sind.

Die Eigenwerte für diesen Fall treten also dort auf, wo sich die beiden Kurven schneiden. Wir haben die ersten fünf auf dem Graphen dargestellt, und wie wir festgestellt haben, ist das, was auf dem Graphen zu sehen ist, in Wirklichkeit die Quadratwurzel des tatsächlichen Eigenwerts.
Interessant ist hier, dass die Eigenwerte umso näher an die Asymptoten der Tangente herankommen, je weiter außen auf dem Graphen sie liegen, und wir machen uns das zunutze und sagen, dass wir die Eigenwerte für ausreichend große \(n\) mit den (sehr gut bekannten) Positionen der Asymptoten der Tangente annähern können.
Wie groß der Wert von \(n\) ist, bevor wir mit der Annäherung beginnen, hängt davon ab, wie genau wir sein wollen, aber da wir die Lage der Asymptoten kennen und die Genauigkeit der Annäherung mit steigendem \(n\) zunimmt, ist es einfach genug, eine bestimmte Genauigkeit zu überprüfen.
Für die Zwecke dieses Beispiels haben wir die ersten fünf numerisch gefunden und verwenden dann die Annäherung der restlichen Eigenwerte. Hier sind diese Werte/Annäherungen.
Die Zahl in Klammern nach den ersten fünf ist der ungefähre Wert der Asymptote. Wie wir sehen können, liegen sie ein wenig daneben, aber bis wir zu \(n = 5\) kommen, beträgt der Fehler in der Annäherung 0,9862%. Bei \(n = 5\) beträgt der Fehler also weniger als 1 %, und er wird nur besser, wenn der Wert von \(n\) größer wird.
Die Eigenfunktionen für diesen Fall sind,
\
wobei die Werte von \({\lambda _{\,n}}\) oben angegeben sind.
So, jetzt, wo die ganze Arbeit erledigt ist, schauen wir uns den zweiten Fall an.
\(\underline {\lambda = 0} \)
Die allgemeine Lösung ist,
\
Die Anwendung der ersten Randbedingung ergibt,
\
Damit ist die allgemeine Lösung dann,
\
Wenn man die zweite Randbedingung darauf anwendet, erhält man,
\
Daher erhalten wir für diesen Fall nur die triviale Lösung, und \(\lambda = 0\) ist also kein Eigenwert. Wäre die zweite Randbedingung jedoch \(y’\links( 1 \rechts) – y\links( 1 \rechts) = 0\) gewesen, dann wäre \(\lambda = 0\) ein Eigenwert (mit Eigenfunktionen \(y\links( x \rechts) = x\)), und wir müssen also auch hier vorsichtig sein, nicht zu viel in unsere Arbeit hineinzulesen.
Schließlich kümmern wir uns um den dritten Fall.
\(\underline {\lambda < 0} \)
Die allgemeine Lösung ist hier,
\
Die Anwendung der ersten Randbedingung ergibt,
\
Damit wird die allgemeine Lösung,
\
Wenn man die zweite Randbedingung anwendet, erhält man,
\
Nun wissen wir durch die Annahme, dass \(\lambda < 0\) und somit \(\sqrt { – \lambda } > 0\). Dies wiederum sagt uns, dass \(\sinh \left( {\sqrt { – \lambda } } \right) > 0\) und wir wissen, dass \(\cosh \left( x \right) > 0\) für alle \(x\). Daher
\
und so müssen wir \({c_2} = 0\) haben und wieder einmal in diesem dritten Fall erhalten wir die triviale Lösung und so wird dieses BVP keine negativen Eigenwerte haben.
Zusammengefasst ergeben sich die einzigen Eigenwerte für dieses BVP aus der Annahme, dass \(\lambda > 0\) und sie sind oben angegeben.
So, wir haben in diesem Abschnitt mehrere Beispiele für Eigenwerte/Eigenfunktionen bearbeitet. Bevor wir diesen Abschnitt verlassen, müssen wir noch einmal darauf hinweisen, dass es eine Vielzahl von verschiedenen Problemen gibt, die wir hier bearbeiten können, und wir haben wirklich nur eine Handvoll Beispiele gezeigt, also gehen Sie bitte nicht in dem Glauben aus diesem Abschnitt, dass wir Ihnen alles gezeigt haben.
Der ganze Zweck dieses Abschnitts ist es, uns auf die Arten von Problemen vorzubereiten, die wir im nächsten Kapitel sehen werden. Auch im nächsten Kapitel werden wir uns wieder auf einige recht grundlegende und einfache Probleme beschränken, um eine der gebräuchlichsten Methoden zum Lösen partieller Differentialgleichungen zu veranschaulichen.
Leave a Reply