Articles /

Matematik for de liberale kunstarter

Læringsresultater

  • Definere og identificere selvlignende egenskaber i geometriske former, planter, og geologiske formationer
  • Generere en fraktal form givet en initiator og en generator
  • Skalere et geometrisk objekt med en specifik skaleringsfaktor ved hjælp af relationen mellem skaleringsdimensionen
  • Bestemme den fraktale dimension af et fraktalt objekt

Ud over visuel selvligartethed udviser fraktaler andre interessante egenskaber. Læg f.eks. mærke til, at hvert trin i Sierpinski-pakningens iteration fjerner en fjerdedel af det resterende areal. Hvis denne proces fortsættes i det uendelige, vil vi ende med stort set at fjerne hele arealet, hvilket betyder, at vi startede med et 2-dimensionelt areal og på en eller anden måde ender med noget mindre end det, men tilsyneladende mere end blot en 1-dimensionel linje.

For at udforske denne idé er vi nødt til at diskutere dimension. Noget som en linje er 1-dimensionalt; den har kun længde. Enhver kurve er 1-dimensionel. Ting som kasser og cirkler er 2-dimensionelle, da de har længde og bredde, hvilket beskriver et område. Genstande som kasser og cylindre har længde, bredde og højde, hvilket beskriver et rumfang, og er 3-dimensionelle.

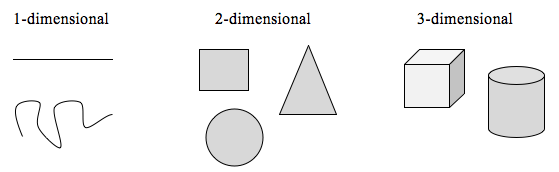
1-dimensionelle genstande omfatter en lige linje og en uregelmæssig bølgelinje. 2-dimensionelle genstande omfatter et rektangel, en trekant og en cirkel. 3-dimensionelle objekter omfatter en terning og en cylinder.

Visse regler gælder for skalering af objekter, relateret til deres dimension.

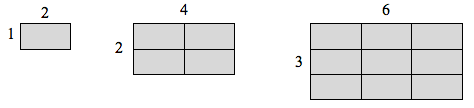
Hvis jeg havde en linje med længde 1, og ville skalere dens længde med 2, ville jeg have brug for to kopier af den oprindelige linje. Hvis jeg havde en linje med længde 1, og ønskede at skalere dens længde med 3, ville jeg have brug for tre kopier af originalen.

1, en vandret linje. 2, en vandret linje, der er dobbelt så lang. 3, en vandret linje, der er tre gange så lang.

Hvis jeg havde et rektangel med længde 2 og højde 1 og ønskede at skalere dets længde og bredde med 2, ville jeg have brug for fire kopier af det oprindelige rektangel. Hvis jeg ville skalere længden og bredden med 3, ville jeg have brug for ni kopier af det oprindelige rektangel.

Et rektangel med siderne, der måler 1 og 2. Dernæst fire kopier af dette rektangel for at danne et større rektangel med sidemålene 2 og 4. Dernæst ni kopier af det første rektangel for at danne et større rektangel med siderne 3 og 6.

Hvis jeg havde en kubisk kasse med siderne af længde 1 og ønskede at skalere dens længde og bredde med 2, ville jeg have brug for otte kopier af den oprindelige kube. Hvis jeg ville skalere længden og bredden med 3, ville jeg have brug for 27 kopier af den oprindelige terning.

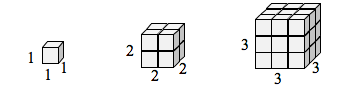
En terning med siderne målt 1 x 1 x 1 x 1. Dernæst otte kopier af denne terning for at danne en større terning med siderne målt 2 x 2 x 2 x 2. Dernæst 27 kopier af den oprindelige terning for at danne en større terning målt 3 x 3 x 3 x 3.

Bemærk, at i det 1-dimensionelle tilfælde er de nødvendige kopier = skala.

I det 2-dimensionelle tilfælde er de nødvendige kopier = skala^{2}.

I det 3-dimensionelle tilfælde er de nødvendige kopier = skala^{3}.

Fra disse eksempler kan vi udlede et mønster.

Skalering-dimension-relation

For at skalere en D-dimensionel form med en skaleringsfaktor S, vil antallet af nødvendige kopier C af den oprindelige form være givet ved:

\text{Kopier}=\text{Skala}^{\text{Dimension}}}, eller C=S^{D}

Eksempel

Anvend skala-dimension-relationen til at bestemme dimensionen af Sierpinski-pakningen.

Sæt, at vi definerer den oprindelige pakning til at have sidelængden 1. Den viste større pakning er dobbelt så bred og dobbelt så høj, så den er blevet skaleret med en faktor 2.

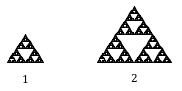
Sierpinski pakningstrekant. Dernæst en større trekant bestående af tre Sierpinski-kassetrekanter og en hvid trekant i midten.

Bemærk, at for at konstruere den større kasse er der brug for 3 eksemplarer af den oprindelige kasse.

Ved anvendelse af skalerings-dimensionsrelationen C=S^{D} får vi ligningen 3=2^{D}.

Da 2^{1}=2 og 2^{2}=4, kan vi straks se, at D ligger et sted mellem 1 og 2; pakningen er mere end en 1-dimensionel form, men vi har fjernet så meget areal, at det nu er mindre end 2-dimensionelt.

Løsningen af ligningen 3=2^{D} kræver logaritmer. Hvis du har studeret logaritmer tidligere, kan du måske huske, hvordan du løser denne ligning (hvis ikke, kan du bare springe til boksen nedenfor og bruge denne formel med log-tasten på en lommeregner):

Tag logaritmen af begge sider.

3={{{2}^{D}}}

Brug eksponentegenskaben for logaritmer.

\log(3)=\log\venstre({{2}^{D}}}\højre)

Divider med log(2).

\log(3)=D\log\left(2\right)

Dimensionen af pakningen er ca. 1,585.

D=\frac{\log\left(3\right)}{\log(2)}\cirka1.585

Skalering-dimension-relation, for at finde dimensionen

For at finde dimensionen D af en fraktal skal du bestemme skaleringsfaktoren S og det nødvendige antal kopier C af den oprindelige form, brug derefter formlen

D=\frac{\log\venstre(C\højre)}{\log(S)}

Afprøv det

Bestem den fraktale dimension af den fraktal, der er fremstillet ved hjælp af initiatoren og generatoren.

Initiatoren er en firkant. Generator er fem firkanter, der danner et ternet mønster.
Vis løsning

Skalering af fraktalen med en faktor 3 kræver 5 kopier af originalen.

D=\frac{\text{log}\left(5\right)}{\text{log}\left(3\right)}\approx1.465

I den følgende video præsenterer vi et gennemarbejdet eksempel på, hvordan man kan bestemme dimensionen af Sierpinski pakningen

Leave a Reply