Indledning til dekonvolution

Dekonvolution er en beregningsintensiv billedbehandlingsteknik, der i stigende grad anvendes til at forbedre kontrasten og opløsningen af digitale billeder, der er optaget i mikroskopet. Grundlaget er baseret på en række metoder, der er designet til at fjerne eller vende den sløring, der er til stede i mikroskopbilleder, og som er induceret af objektivets begrænsede åbning.

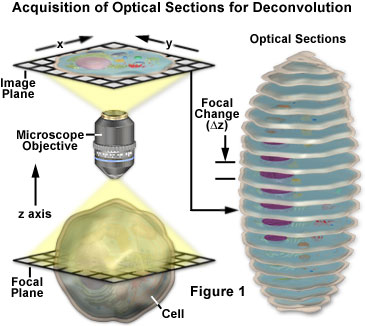
Næsten ethvert billede, der er optaget i et digitalt fluorescensmikroskop, kan dekonvolutioneres, og der er ved at blive udviklet flere nye applikationer, der anvender dekonvolutionsteknikker på billeder af transmitteret lys, der er opsamlet under en række forskellige kontrastforbedrende strategier. Blandt de mest velegnede emner til forbedring ved hjælp af dekonvolution er tredimensionelle montager konstrueret af en række optiske snit.

De grundlæggende koncepter omkring erhvervelse af z-seriebilleder til dekonvolutionsanalyse er præsenteret med et skematisk diagram i figur 1. Der optages en række billeder af prøven, som hver især er forskudt en smule fra hinanden langs z-aksen. Denne ændring af fokusplanet resulterer i et lidt anderledes billede med subtile ændringer forårsaget af ufokuseret lys, der kommer fra over og under det aktuelle z-plan. Under dekonvolutionsanalysen analyseres hele z-serien for at skabe et klarere datasæt med højere opløsning, der ikke er forvirret af fluorescens uden for fokus.

Dekonvolution foreslås ofte som et godt alternativ til det konfokale mikroskop, da begge teknikker søger at minimere effekten af fluorescens uden for fokus på dit endelige billede… Dette er ikke strengt taget sandt, fordi billeder, der er erhvervet ved hjælp af en pinhole-åbning i et konfokalt mikroskop, drager fordel af dekonvolutionsbehandling. Ved konfokal mikroskopi forhindres ufokuseret lys i at blive registreret ved at placere en pinhole-åbning mellem objektivet og detektoren, hvorigennem kun lysstråler, der er i fokus, kan passere. I modsætning hertil tillader widefield-mikroskoper, at ufokuseret lys kan passere direkte til detektoren. Deconvolution anvendes derefter på de resulterende billeder for enten at subtrahere det ufokuserede lys eller for at henføre det tilbage til dets kilde. Konfokal mikroskopi er særlig velegnet til undersøgelse af tykke eksemplarer som f.eks. embryoner eller tussager, mens widefield-dekonvolutionsbehandling har vist sig at være et effektivt værktøj til afbildning af eksemplarer, der kræver ekstremt lavt lysniveau. Disse værktøjer kan endda kombineres for at reducere støjen i billeder, der er optaget med et konfokalt mikroskop. Størstedelen af de dekonvolutionseksperimenter, der er rapporteret i litteraturen, gælder dog for billeder, der er optaget på et standard widefield fluorescensmikroskop.

Kilder til billedforringelse

Billedforringelse kan opdeles i fire uafhængige kilder: støj, spredning, blænding og uskarphed. Figur 2 viser eksempler på den visuelle påvirkning af hver af disse på det samme billede.

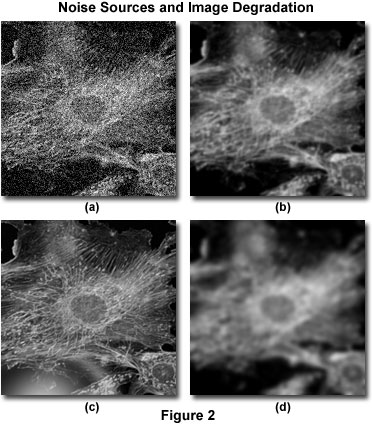
Støj kan beskrives som en næsten tilfældig forstyrrelse af detaljerne i et billede, som (i sin alvorligste form) har udseende som hvid støj eller salt-og-peber-støj, svarende til det, der ses i tv-udsendelser ved dårlig modtagelse (Figur 2(a)). Denne type støj betegnes som “kvasi-tilfældig”, fordi den statistiske fordeling kan forudsiges, hvis man kender kildens mekanik. I digital mikroskopi er hovedkilden til støj enten selve signalet (ofte omtalt som fotonskudsstøj) eller det digitale billeddannelsessystem. Begge støjkildernes mekanik er kendt, og derfor er den statistiske fordeling af støjen kendt. Signalafhængig støj kan karakteriseres ved en Poisson-fordeling, mens støj, der stammer fra billeddannelsessystemet, ofte følger en Gauss-fordeling. Fordi kilden til og fordelingen af almindelig støj i digitale billeder er så velforstået, kan den let fjernes ved anvendelse af de relevante billedfiltre, som normalt indgår i de fleste dekonvolutionssoftwarepakker som en valgfri “forbehandlingsrutine”.

Spredning betegnes normalt som en tilfældig forstyrrelse af lyset, der fremkaldes af ændringer i brydningsindekset i en prøve. Nettoeffekten af spredning er en virkelig tilfældig forstyrrelse af billeddetaljerne, som det fremgår af figur 2(b). Selv om der ikke er udviklet nogen helt tilfredsstillende metode til at forudsige spredningen i en given prøve, er det blevet påvist, at graden af spredning er stærkt afhængig af prøvens tykkelse og de optiske egenskaber ved prøven og de omgivende indlejringsmaterialer. Spredningen øges både med prøvens tykkelse og med heterogeniteten af det brydningsindeks, som de interne komponenter i prøven udgør.

Som spredning er blænding en tilfældig forstyrrelse af lyset, men den opstår i mikroskopets optiske elementer (linser, filtre, prismer osv.) snarere end i prøven. Niveauet af blænding i et moderne mikroskop er blevet minimeret ved at anvende linser og filtre med antireflekterende belægninger og ved at forfine linsedannelsesmetoderne, optiske cementer og glasformuleringer. Figur 2(c) illustrerer virkningen af ukontrolleret blænding.

Blur beskrives ved en ikke-tilfældig spredning af lyset, som opstår ved passage gennem billeddannelsessystemets optiske vej (figur 2(d)). Den vigtigste kilde til sløring er diffraktion, og et billede, hvis opløsning kun begrænses af sløring, anses for at være diffraktionsbegrænset. Dette er en iboende grænse for ethvert billeddannelsessystem og er den afgørende faktor ved vurderingen af opløsningsgrænsen for et optisk system. Heldigvis findes der sofistikerede modeller for sløring i et optisk mikroskop, som kan anvendes til at bestemme kilden til fotoner uden for fokus. Dette er grundlaget for dekonvolution. På grund af dens grundlæggende betydning for dekonvolution vil den teoretiske model for sløring blive diskuteret meget mere detaljeret i andre dele af dette afsnit. Det skal dog understreges, at alle billeddannelsessystemer frembringer sløring uafhængigt af andre former for billedforringelse forårsaget af prøven eller den ledsagende instrumentelle elektronik. Det er netop denne uafhængighed af optisk sløring i forhold til andre former for forringelse, der gør det muligt at fjerne sløring ved hjælp af dekonvolutionsteknikker.

Interaktionen mellem lys og stof er den primære fysiske årsag til spredning, blænding og sløring. Men sammensætningen og arrangementet af molekyler i et givet materiale (uanset om det er glas, vand eller protein) giver hvert materiale sit eget særlige sæt af optiske egenskaber. I forbindelse med dekonvolution er det, der adskiller spredning, blænding og sløring, det sted, hvor de forekommer, og muligheden for at generere en matematisk model for disse fænomener. Da spredning er et lokalt, uregelmæssigt fænomen, der forekommer i prøven, har det vist sig vanskeligt at modellere det. Da sløring derimod er en funktion af det optiske system i mikroskopet (hovedsagelig objektivet), kan det modelleres relativt enkelt. En sådan model gør det muligt at vende sløringsprocessen matematisk, og dekonvolution anvender denne model til at vende eller fjerne sløring.

Punktspredningsfunktionen

Den model for sløring, der har udviklet sig i teoretisk optik, er baseret på begrebet en tredimensional punktspredningsfunktion (PSF). Dette begreb er af grundlæggende betydning for dekonvolution og bør forstås klart og tydeligt for at undgå billeddannelsesartefakter. Punktspredningsfunktionen er baseret på en uendelig lille punktkilde af lys med oprindelse i prøveområdet (objektet). Da mikroskopets billeddannelsessystem kun opfanger en brøkdel af det lys, der udsendes af dette punkt, kan det ikke fokusere lyset til et perfekt tredimensionalt billede af punktet. I stedet vises punktet udvidet og spredt i et tredimensionalt diffraktionsmønster. Således defineres punktspredningsfunktionen formelt som det tredimensionelle diffraktionsmønster, der genereres af en ideel punktkilde af lys.

Afhængigt af den anvendte billeddannelsesmetode (widefield, konfokal, transmitteret lys) har punktspredningsfunktionen en anden og unik form og kontur. I et widefield fluorescensmikroskop ligner formen af punktspredningsfunktionen en aflang “fodbold” af lys omgivet af en flare af udvidende ringe. For at beskrive punktspredningsfunktionen i tre dimensioner er det almindeligt at anvende et koordinatsystem med tre akser (x, y og z), hvor × og y er parallelle med prøvens brændpunktsplan, og z er parallel med mikroskopets optiske akse. I dette tilfælde fremstår punktspredningsfunktionen som et sæt koncentriske ringe i x-y-planet og ligner et timeglas i x-z- og y-z-planet (som illustreret i figur 3). Et x-y snit gennem centrum af bredfelts punktspredningsfunktionen afslører et sæt koncentriske ringe: den såkaldte Airy-skive, som der almindeligvis henvises til i tekster om klassisk optisk mikroskopi.

To x-z-projektioner af punktspredningsfunktioner, der viser forskellige grader af sfærisk aberration, er vist i figur 3. Den optiske akse er parallel med billedets lodrette akse. Den punktspredningsfunktion til venstre viser minimal sfærisk aberration, mens den til højre viser en betydelig grad af aberration. Bemærk, at den aksiale asymmetri og udvidelsen af det centrale knudepunkt langs den optiske akse i det højre billede fører til en forringet aksial opløsning og en sløring af signalet. I teorien er størrelsen af punktspredningsfunktionen uendelig, og den samlede summerede lysintensitet i planer langt fra fokus er lig med den summerede intensitet ved fokus. Lysintensiteten falder imidlertid hurtigt og kan til sidst ikke længere skelnes fra støj. I en uaberrated punktspredningsfunktion, der er optaget med et olieimmersionsobjektiv med høj numerisk apertur (1,40), spredes lys, der fylder 0,2 kvadratmikrometer i fokusplanet, over 90 gange dette område 1 mikrometer over og under fokus. Prøven, der blev anvendt til at optage disse billeder af punktspredningsfunktionen, var en fluorescerende perle med en diameter på 0,1 mikrometer monteret i glycerol (brydningsindeks lig med 1,47), med immersionsolier med de brydningsindeks, der er angivet i figuren.

En vigtig overvejelse er, hvordan punktspredningsfunktionen påvirker billeddannelsen i mikroskopet. I den teoretiske model for billeddannelse behandles punktspredningsfunktionen som den grundlæggende enhed i et billede. Med andre ord er punktspredningsfunktionen for billedet, hvad murstenene er for huset. Det bedste, et billede nogensinde kan være, er en samling af punktspredningsfunktioner, og en forøgelse af forstørrelsen vil ikke ændre dette faktum. Som en kendt lærebog i teoretisk optik (Born og Wolf: Principles of Optics) forklarer: “Det er umuligt at fremhæve detaljer, der ikke er til stede i det primære billede, ved at øge okularets styrke, for hvert element i det primære billede er et lille diffraktionsmønster, og det faktiske billede, som det ses af okularet, er kun en sammensætning af de forstørrede billeder af disse mønstre”.

Som eksempel kan man overveje en population af subopløselige fluorescerende perler, der er anbragt mellem et dækglas og et mikroskopglas. Et fokuseret billede af dette eksemplar afslører en sky af prikker, som i virkeligheden er en skive omgivet af et lille sæt ringe (i virkeligheden en Airy-skive; se figur 4(a)). Hvis dette eksemplar fjernes en smule fra fokus, vises et større sæt koncentriske ringe på det sted, hvor hver enkelt prik var i det fokuserede billede (figur 4(b)). Når der indsamles et tredimensionelt billede af dette eksemplar, registreres en komplet punktspredningsfunktion for hver perle. Punktspredningsfunktionen beskriver, hvad der sker med hver enkelt punktkilde af lys, efter at den er passeret gennem billeddannelsessystemet.

Den netop beskrevne sløringsproces er matematisk modelleret som en konvolution. Foldningsoperationen beskriver anvendelsen af punktspredningsfunktionen på hvert punkt i prøven: lys, der udsendes fra hvert punkt i objektet, foldes med punktspredningsfunktionen for at frembringe det endelige billede. Desværre medfører denne konvolution, at punkterne i prøven bliver til slørede områder i billedet. Lysstyrken af hvert punkt i billedet er ved hjælp af konvolutionen lineært forbundet med fluorescensen af hvert punkt i prøven. Da punktspredningsfunktionen er tredimensionel, er sløring fra punktspredningsfunktionen et iboende tredimensionelt fænomen. Billedet fra et hvilket som helst fokusplan indeholder sløret lys fra punkter placeret i dette plan blandet sammen med sløret lys fra punkter med oprindelse i andre fokusplaner.

Situationen kan sammenfattes med den idé, at billedet dannes ved en konvolution af prøven med punktspredningsfunktionen. Dekonvolution vender denne proces om og forsøger at rekonstruere prøven ud fra et sløret billede.

Aberrationer i punktspredningsfunktionen

Punktspredningsfunktionen kan defineres enten teoretisk ved hjælp af en matematisk diffraktionsmodel eller empirisk ved at optage et tredimensionelt billede af en fluorescerende perle (se figur 3). En teoretisk punktspredningsfunktion har generelt aksial og radial symmetri. Det vil sige, at punktspredningsfunktionen er symmetrisk over og under x-y-planet (aksial symmetri) og roterende omkring z-aksen (radial symmetri). En empirisk punktspredningsfunktion kan afvige betydeligt fra perfekt symmetri (som vist i figur 3). Denne afvigelse, der almindeligvis kaldes aberration, skyldes uregelmæssigheder eller fejljusteringer i en hvilken som helst komponent i det optiske system til billeddannelse, især objektivet, men kan også forekomme i forbindelse med andre komponenter såsom spejle, strålesplittere, rørlinser, filtre, membraner og blænder. Jo bedre kvaliteten af de optiske komponenter er, og jo bedre mikroskopet er justeret, jo tættere kommer den empiriske punktspredningsfunktion på sin ideelle symmetriske form. Både konfokal- og dekonvolutionsmikroskopi er afhængig af, at punktspredningsfunktionen er så tæt på idealtilfældet som muligt.

Den mest almindelige aberration, som man støder på i optisk mikroskopi, og som er velkendt for enhver erfaren og professionel mikroskopiker, er sfærisk aberration. Denne aberration viser sig ved en aksial asymmetri i punktspredningsfunktionens form med en tilsvarende stigning i størrelsen, især langs z-aksen (figur 3). Resultatet er et betydeligt tab af opløsning og signalintensitet. I praksis er den typiske kilde til sfærisk aberration en uoverensstemmelse mellem brydningsindekset for objektivets frontlinse og det indstøbningsmedium, som prøven er badet i. Der bør lægges stor vægt på vigtigheden af at minimere denne aberration. Selv om dekonvolution delvist kan genoprette den tabte opløsning, kan ingen billedbehandling genoprette det tabte signal.