Indførelse af konsistent Hashing

Med fremkomsten af distribuerede arkitekturer, blev konsistent hashing mainstream. Men hvad er det egentlig, og hvordan adskiller det sig fra en standard hashing-algoritme? Hvad er de nøjagtige motiveringer bag den?

Først vil vi beskrive de vigtigste begreber. Derefter vil vi grave i eksisterende algoritmer for at forstå de udfordringer, der er forbundet med konsistent hashing.

Hashing

Hashing er processen til at kortlægge data af vilkårlig størrelse til værdier af fast størrelse. Hver eksisterende algoritme har sin egen specifikation:

• MD5 producerer 128-bit hashværdier.
• SHA-1 producerer 160-bit hashværdier.
• etc.

Hashing har mange anvendelser inden for datalogi. En af disse anvendelser kaldes f.eks. checksumme. For at verificere integriteten af et datasæt er det muligt at anvende en hashing-algoritme. En server hasher et datasæt og angiver hash-værdien til en klient. Derefter hasher klienten sin version af datasættet og sammenligner hashværdierne. Hvis de er ens, bør integriteten verificeres.

Det “bør” her er vigtigt. Det værst tænkelige scenarie er, når der opstår en kollision. En kollision er, når to forskellige data har den samme hash-værdi. Lad os tage et eksempel fra det virkelige liv ved at definere følgende hashing-funktion: Givet en person returnerer den hans fødselsdagsdato (dag & fødselsmåned). Fødselsdagsparadokset fortæller os, at hvis der kun er 23 personer i et rum, er sandsynligheden for, at to personer har den samme fødselsdag (og dermed en kollision), over 50 %. Derfor er fødselsdagsfunktionen sandsynligvis ikke en god hashing-funktion.

Som en hurtig introduktion til hashing er det vigtigt at forstå, at hovedidéen handler om at sprede værdier over et domæne. For eksempel:

• MD5 spreder værdier over et 128-bit rumdomæne
• En hashtable (eller hashmap), der understøttes af et array med 32 elementer, har en intern hashing-funktion, der spreder værdier til ethvert indeks (fra 0 til 31).

Lastfordeling

Lastfordeling kan defineres som processen med at sprede belastning på tværs af knudepunkter. Udtrykket node kan her udskiftes med server eller instans. Det er en beregningsenhed.

Load balancing er et eksempel på belastningsfordeling. Det drejer sig om at fordele et sæt opgaver over et sæt ressourcer. Vi bruger f.eks. load balancing til at fordele API-forespørgsler amont webserverinstanser.

Når det drejer sig om data, bruger vi hellere udtrykket sharding. En database shard er en horisontal partition af data i en database. Et typisk eksempel er en database, der er opdelt i tre shards, hvor hver shard har en delmængde af de samlede data.

Load balancing og sharding deler nogle fælles udfordringer. Spredning af data jævnt for eksempel for at sikre, at en knude ikke bliver overbelastet i forhold til de andre. I nogle sammenhænge skal load balancing og sharding også fortsat tilknytte opgaver eller data til den samme node:

• Hvis vi skal serialisere, håndtere en efter en, operationerne for en given forbruger, skal vi videresende anmodningen til den samme node.
• Hvis vi skal fordele data, skal vi vide, hvilken shard der er ejer for en bestemt nøgle.

Lyder det bekendt? I disse to eksempler spreder vi værdier over et domæne. Hvad enten det er en opgave, der spredes til serverknuder, eller data, der spredes til database shard, finder vi tilbage til ideen forbundet med hashing. Dette er grunden til, at hashing kan bruges i forbindelse med belastningsfordeling. Lad os se hvordan.

Mod-n Hashing

Princippet for mod-n hashing er følgende. Hver nøgle hashes ved hjælp af en hashing-funktion til at omdanne et input til et heltal. Derefter udfører vi en modulo baseret på antallet af knuder.

Lad os se et konkret eksempel med 3 knuder. Her skal vi fordele belastningen mellem disse knuder på baggrund af en nøgleidentifikator. Hver nøgle hashes, hvorefter vi udfører en modulo-operation:

Fordelen ved denne tilgang er dens tilstandsløshed. Vi behøver ikke at bevare nogen tilstand for at minde os om, at foo blev videresendt til knude 2. Alligevel skal vi vide, hvor mange knuder der er konfigureret til at anvende modulo-operationen.

Hvordan fungerer mekanismen så i tilfælde af ud- eller indskalering (tilføjelse eller fjernelse af knuder)? Hvis vi tilføjer endnu en knude, er modulo-operationen nu baseret på 4 i stedet for 3:

Som vi kan se, er nøglerne foo og baz ikke længere knyttet til den samme knude. Med mod-n hashing er der ingen garanti for at opretholde nogen konsistens i tilknytningen nøgle/knude. Er dette et problem? Det kan det måske.

Hvad sker der, hvis vi implementerer et datastore ved hjælp af sharding og baseret på mod-n-strategien til at distribuere data? Hvis vi skalerer antallet af knuder, skal vi udføre en rebalancering. I det foregående eksempel betyder rebalancering:

• Flytning af foo fra knude 2 til knude 0.
• Flytning af baz fra knude 2 til knude 3.

Hvad sker der nu, hvis vi havde lagret millioner eller endda milliarder af data, og at vi har brug for at rebalancere næsten alt? Som vi kan forestille os, ville det være en tung proces. Derfor skal vi ændre vores belastningsfordelingsteknik for at sikre, at vi ved rebalancering:

• Fordelingen forbliver så ensartet som muligt baseret på det nye antal knudepunkter.
• Antallet af nøgler, som vi skal migrere, bør være begrænset. Ideelt set ville det kun være 1/n procent af nøglerne, hvor n er antallet af knuder.

Det er præcis formålet med konsistente hashing-algoritmer.

Begrebet konsistent kan dog være noget forvirrende. Jeg mødte ingeniører, der gik ud fra, at sådanne algoritmer blev ved med at knytte en given nøgle til den samme knude, selv i lyset af skalerbarhed. Dette er ikke tilfældet. Den skal være konsistent indtil et vist punkt for at holde fordelingen ensartet.

Nu er det tid til at grave i nogle løsninger.

Rendezvous

Rendezvous var den første algoritme, der nogensinde blev foreslået til at løse vores problem. Selv om den oprindelige undersøgelse, der blev offentliggjort i 1996, ikke nævnte udtrykket “consistent hashing”, giver den en løsning på de udfordringer, vi beskrev. Lad os se en mulig implementering i Go:

Hvordan fungerer den? Vi gennemløber hver knude og beregner dens hash-værdi. Hashværdien returneres af en hash-funktion, der producerer et heltal baseret på en nøgle (vores input) og en nodeidentifikator (den nemmeste tilgang er at hashe sammenkædningen af de to strenge). Derefter returnerer vi den node med den højeste hashværdi. Dette er grunden til, at algoritmen også er kendt som hashing med højeste tilfældige vægt.

Den største ulempe ved rendezvous er dens O(n)-tidskompleksitet, hvor n er antallet af knuder. Den er meget effektiv, hvis vi har brug for at have et begrænset antal knuder. Men hvis vi begynder at vedligeholde tusindvis af knuder, kan det begynde at give problemer med ydeevnen.

Ring Consistent Hash

Den næste algoritme blev frigivet i 1997 af Karger et al. i denne artikel. I denne undersøgelse nævnes for første gang udtrykket consistent hashing.

Den er baseret på en ring (en end-to-end forbundet matrix). Selv om det er den mest populære konsistente hashing-algoritme (eller i det mindste den mest kendte), er princippet ikke altid velforstået. Lad os dykke ned i det.

Den første operation er at oprette ringen. En ring har en fast længde. I vores eksempel opdeler vi den i 12 dele:

Dernæst placerer vi vores knuder. I vores eksempel vil vi definere N0, N1 og N2.

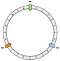
Noderne fordeles jævnt indtil videre. Vi vender tilbage til dette punkt senere.

Derpå er det tid til at se på, hvordan nøglerne skal repræsenteres. Først har vi brug for en funktion f, der returnerer et ringindeks (fra 0 til 11) baseret på en nøgle. Vi kan bruge mod-n hashing til det. Da ringlængden er konstant, vil det ikke volde os nogen problemer.

I vores eksempel vil vi definere 3 nøgler: a, b og c. Vi anvender f på hver af dem. Lad os antage, at vi har følgende resultater:

• f(a) = 1
• f(a) = 5
• f(a) = 7

Så kan vi placere nøglerne på ringen på denne måde:

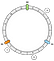
Hvordan tilknytter vi en given nøgle til en node? Den vigtigste logik er at bevæge sig fremad. Fra en given nøgle returnerer vi den første knude, som vi finder næste gang, mens vi bevæger os fremad:

I dette eksempel tilknytter vi a til N1, b og c til N2.

Nu skal vi se, hvordan rebalancering håndteres. Vi definerer endnu et knudepunkt N3. Hvor skal vi placere den? Der er ikke længere plads til, at den samlede fordeling skal være ensartet. Skal vi omorganisere knuderne? Nej, ellers ville vi jo ikke længere være ensartede, ikke sandt? For at placere en node genbruger vi den samme hashing-funktion f, som vi introducerede. I stedet for at blive kaldt med en nøgle kan den kaldes med en nodeidentifikator. Så placeringen af den nye node bestemmes tilfældigt.

Der opstår så et spørgsmål: Hvad skal vi gøre med a, da den næste knude ikke længere er N1:

Løsningen er følgende: Vi skal ændre dens tilknytning og få a tilknyttet N3:

Som vi diskuterede tidligere, bør en ideel algoritme ombalancere 1/n procent af nøglerne i gennemsnit. I vores eksempel, da vi tilføjer en fjerde knude, bør vi have 25 % af de mulige nøgler omforbundet til N3. Er dette tilfældet?

• N0 fra indeks 8 til 12: 33,3 pct. af de samlede nøgler
• N1 fra indeks 2 til 4: 16,6 pct. af de samlede nøgler
• N2 fra indeks 4 til 8: 33.3% af de samlede nøgler
• N3 fra indeks 0 til 2: 16,6% af de samlede nøgler

Denne fordeling er ikke ensartet. Hvordan kan vi forbedre det? Løsningen er at bruge virtuelle knuder.

Lad os sige, at vi i stedet for at placere et enkelt punkt pr. knude kan placere tre i stedet. Desuden skal vi definere tre forskellige hashing-funktioner. Hver knude hashes tre gange, så vi får tre forskellige indeks:

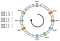
Vi kan anvende den samme algoritme ved at bevæge os fremad. Dog ville en nøgle blive tilknyttet en knude uanset hvilken virtuel knude den mødte.

I netop dette eksempel ville fordelingen nu være følgende:

• N0: 33,3 %
• N1: 25 %
• N2: 41,6 %

Desto flere virtuelle knuder vi definerer pr. knude, jo mere ensartet skulle fordelingen være. I gennemsnit med 100 virtuelle knuder pr. server er standardfordelingen ca. 10 %. Med 1000 er den ca. 3,2 %.

Denne mekanisme er også nyttig, hvis vi har knuder med forskellige størrelser. Hvis en knude f.eks. er konfigureret til teoretisk set at kunne håndtere to gange så stor belastning som de andre, kan vi spinne dobbelt så mange virtuelle knuder.

Den største ulempe ved de virtuelle knuder er dog hukommelsesaftrykket. Hvis vi skal håndtere tusindvis af servere, ville det kræve megabyte hukommelse.

Hvor vi går videre, er det interessant at bemærke, at en algoritme nogle gange kan forbedres væsentligt ved at ændre en lille del. Dette er f.eks. tilfældet med en algoritme offentliggjort af Google i 2017 kaldet consistent hashing with bounded loads (konsistent hashing med afgrænsede belastninger). Denne version er baseret på den samme ringidé, som vi beskrev. Alligevel er deres tilgang at foretage en lille afbalancering ved enhver opdatering (en ny nøgle eller knude, der tilføjes/slettes). Denne version udkonkurrerer den oprindelige med hensyn til standardafvigelse med den afvejning af en værste tidskompleksitet.

Jump Consistent Hash

I 2007 offentliggjorde to ingeniører fra Google jump consistent hash. Sammenlignet med den ringbaserede algoritme “kræver denne implementering ingen lagring, er hurtigere og gør et bedre stykke arbejde med at fordele nøglepladsen jævnt mellem buckets og med at fordele arbejdsbyrden jævnt, når antallet af buckets ændres”. Sagt på en anden måde forbedrer den fordelingen af arbejdsbyrden mellem noderne (en bucket er det samme begreb som en node) uden noget hukommelsesoverhead.

Her er algoritmen i C++ (7 linjer kode 🤯):

I ringkonsistent hash var standardafvigelsen med 1000 virtuelle noder ca. 3,2 % med 1000 virtuelle noder. I jump consistent hash har vi ikke længere brug for begrebet virtuelle knuder. Alligevel er standardafvigelsen fortsat mindre end 0,0000001%.

Der er dog en begrænsning. Knuderne skal nummereres fortløbende. Hvis vi har en liste med servere foo, bar og baz, kan vi f.eks. ikke fjerne bar. Alligevel kan vi, hvis vi konfigurerer et datalager, anvende algoritmen til at få shard-indekset baseret på det samlede antal shards. Derfor kan jump consistent hash være nyttig i forbindelse med sharding, men ikke i forbindelse med load balancing.

Hvad er Perfect Consistent Hashing Algorithm?

Da vi nu har en vis erfaring med konsistent hashing, lad os tage et skridt tilbage og se, hvad der ville være den perfekte algoritme:

• Kun 1/n procent af nøglerne ville blive remapped i gennemsnit, hvor n er antallet af knuder.
• En O(n) rumkompleksitet, hvor n er antallet af knuder.
• En O(1) tidskompleksitet pr. indsættelse/fjernelse af en knude og pr. nøgleopslag.
• En minimal standardafvigelse for at sikre, at en knude ikke er overbelastet i forhold til en anden knude.
• Den ville gøre det muligt at tilknytte en vægt til en node for at klare forskellige node dimensioner.
• Den ville tillade vilkårlige node navne (ikke nummereret sekventielt) for at understøtte både load balancing og sharding.

Der findes desværre ikke en sådan algoritme. Baseret på det, vi så:

• Rendezvous har en lineær tidskompleksitet pr. opslag.
• Ring consistent hash har en dårlig minimal standardafvigelse uden begrebet virtuelle knudepunkter. Med virtuelle knuder er rumkompleksiteten O(n*v), hvor n er antallet af knuder og v er antallet af virtuelle knuder pr. knude.
• Jump konsistent hash har ikke en konstant tidskompleksitet, og den understøtter ikke vilkårlige knuder.

Området er stadig åbent, og der er nyere undersøgelser, som er værd at kigge på. For eksempel den multiprobe konsistente hash udgivet i 2005. Den understøtter O(1) rumkompleksitet. Men for at opnå en standardafvigelse på ε kræver den O(1/ε) tid pr. opslag. Hvis vi f.eks. ønsker at opnå en standardafvigelse på mindre end 0,5 %, kræver det, at nøglen skal hashes ca. 20 gange. Derfor kan vi opnå en minimal standardafvigelse, men i bestræbelserne på en højere opslagstidskompleksitet.

Som vi sagde i indledningen, er konsistente hashing-algoritmer blevet mainstream. Det bruges nu i utallige systemer såsom MongoDB, Cassandra, Riak, Akka osv. hvad enten det er i forbindelse med balancering af belastning eller fordeling af data. Men som ofte inden for datalogi har enhver løsning kompromiser.

Som vi taler om kompromiser, kan du, hvis du har brug for en opfølgning, tage et kig på det fremragende indlæg skrevet af Damian Gryski: