Hvad er analytisk geometri?
Hvad er analytisk geometri?
Analytisk geometri er en gren af algebraen, der bruges til at modellere geometriske objekter – punkter, (lige) linjer og cirkler er de mest grundlæggende af disse. Analytisk geometri er en stor opfindelse af Descartes og Fermat.
I plan analytisk geometri defineres punkter som ordnede talpar, f.eks. (x, y), mens de rette linjer igen defineres som de sæt af punkter, der opfylder lineære ligninger, jf. de fremragende redegørelser af D. Pedoe eller D. Brannan m.fl. Set ud fra den analytiske geometri er geometriske aksiomer afledbare sætninger. F.eks. er der for to forskellige punkter (x1, y1) og (x2, y2) en enkelt linje ax + by + c = 0, der går gennem disse punkter. Dens koefficienter a, b, c kan findes (op til en konstant faktor) ud fra det lineære system af to ligninger
| ax1 + by1 + c = 0 ax2 + by2 + c = 0, |
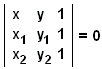 |
Ingen aksiomatisk teori kan dog slippe for at bruge udefinerede elementer. I mængdelæren, der ligger til grund for en stor del af matematikken og især den analytiske geometri, forbliver det mest fundamentale mængdebegreb udefineret.
Geometri af det tredimensionelle rum modelleres med tre taltripler (x, y, z), og en 3D lineær ligning ax + by + cz + d = 0 definerer et plan. Generelt giver den analytiske geometri et praktisk værktøj til at arbejde i højere dimensioner.
Inden for rammerne af den analytiske geometri kan man (og gør det) også modellere ikke-euklidiske geometrier. For eksempel er et punkt i plan projektiv geometri et punkt en tripel af homogene koordinater (x, y, z), ikke alle 0, således at
| (tx, ty, tz) = (x, y, z), |
for alle t ≠ 0, mens en linje er beskrevet ved en homogen ligning
| ax + bx + cz = 0. |
| ax² + bxy + cy² + dx + ey + f = 0. |
Den del af analytisk geometri, der mest omhandler lineære ligninger, kaldes lineær algebra.
Kartesisk analytisk geometri er geometri, hvor akserne x = 0 og y = 0 står vinkelret på hinanden.
Komponenterne i n-tuplen x = (x1, …, xn) kaldes dens koordinater. Når n = 2 eller n = 3, kaldes den første koordinat for abscisse og den anden for ordinat.
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
|Kontakt||Forside||Indhold||Geometri||Op|
Copyright © 1996-2018 Alexander Bogomolny
Leave a Reply