Helmholtz-resonans
- Analyse af Helmholtz-resonansen
- Resonans, impedans, fase- og frekvensafhængighed
- Komplikationer, der involverer længden
- Helmholtz-resonanser og guitarer
Analyse af Helmholtz-resonansen
Lad os nu blive kvantitative: Først og fremmest antager vi, at bølgelængden af den producerede lyd er meget længere end resonatorens dimensioner. For flaskerne i animationen øverst på denne side er bølgelængderne henholdsvis 180 og 74 cm, så denne tilnærmelse er ret god, men det er værd at kontrollere, hver gang man begynder at beskrive noget som en Helmholtz-oscillator. Konsekvensen af denne tilnærmelse er, at vi kan negligere trykvariationer inden for beholderens volumen: trykoscillationen vil have den samme fase overalt inden for beholderen.
Lad luften i halsen have en effektiv længde L og et tværsnitsareal S. Dens masse er da SL gange luftens massefylde ρ. (Nogle komplikationer omkring den effektive længde diskuteres i slutningen af denne side). Hvis denne “prop” af luft falder en lille afstand x ned i flasken, komprimerer den luften i beholderen, således at den luft, der tidligere optog volumen V, nu har volumen V – Sx. Som følge heraf stiger trykket i denne luft fra det atmosfæriske tryk PA til en højere værdi PA + p.
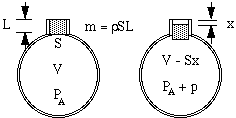
Nu kunne man måske tro, at trykforøgelsen blot ville være proportional med volumenfaldet. Det ville være tilfældet, hvis kompressionen skete så langsomt, at temperaturen ikke ændrede sig. I vibrationer, der giver anledning til lyd, er ændringerne imidlertid hurtige, og derfor stiger temperaturen ved kompressionen, hvilket giver en større ændring i trykket. Teknisk set er de adiabatiske, hvilket betyder, at varmen ikke har tid til at bevæge sig, og den resulterende ligning omfatter en konstant γ, forholdet mellem de specifikke varmegrader, som er ca. 1,4 for luft. (Dette forklares i et appendiks.) Som følge heraf er den trykændring p, som en lille volumenændring ΔV frembringer, blot
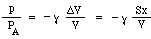
Nu flyttes massen m af forskellen i tryk mellem halsens top og bund, dvs. en nettokraft pS, så vi skriver Newtons lov for accelerationen a:
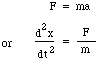
ved at substituere for F og m får man: 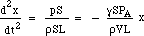
Så den genoprettende kraft er proportional med forskydningen. Dette er betingelsen for simpel harmonisk bevægelse, og den har en frekvens, der er 1/2π gange kvadratroden af proportionalitetskonstanten, så
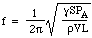
Nu er lydens hastighed c i luft bestemt af densiteten, trykket og forholdet mellem de specifikke varmegrader, så vi kan skrive:
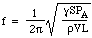
:
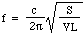
Lad os sætte nogle tal ind: For en 1 liters flaske med S = 3 kvadratcentimeter og L = 5 centimeter er frekvensen 130 Hz, hvilket er omkring C under C i mellemtone C. (Se noter.) Så bølgelængden er 2,6 meter, hvilket er meget større end flasken. Dette retfærdiggør, post hoc, den antagelse, der blev fremsat i begyndelsen af udledningen.
Resonans, impedans, fase- og frekvensafhængighed
Dette afsnit kan læses i sig selv, men hvis du ønsker en mere detaljeret baggrund, kan du se Svingninger, Tvungne svingninger og Akustisk eftergivenhed, inertialitet og impedans.
Lad os vende tilbage til den mekaniske fremstilling og se på Helmholtz-resonatoren udefra, som vist i det første skema: Vi skubber med en svingende kraft F, med frekvensen f ,til massen m (luften i resonatorens hals), som er understøttet af fjederen (den indesluttede luft) med fjederkonstant k, hvis anden ende er fast (luften i resonatoren kan ikke slippe ud). Urealistisk nok negligerer vi tyngdekraften og friktionen (for nu).
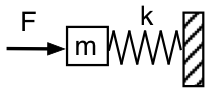
Den kraft, der kræves for at accelerere massen, er proportional med accelerationen og dermed proportional med f2. Ved tilstrækkelig lav frekvens er den kraft, der kræves for at accelerere massen, ubetydelig, så F behøver kun at komprimere og strække fjederen. Så i denne grænse er den påførte kraft F = +kx. (Fjederkraften er -kx.) Systemets mekaniske impedans ved denne lave frekvens er eftergivelig eller fjederlignende. Akustisk set ligner det en akustisk eftergivenhed: Vi skubber luftmassen i halsen og komprimerer luften i resonatoren. Den påførte kraft F til højre er i fase med x målt til højre, så den er 90° bag hastigheden, og det påførte tryk er 90° bag den akustiske strømning ind i resonatoren.
Husk, at f2 er afhængig af accelerationen. Så ved en tilstrækkelig høj frekvens er fjederkraften ubetydelig i forhold til den, der accelererer massen. F er altså i fase med accelerationen, hvilket gør, at den er 90° foran hastigheden. Akustisk set er det påførte tryk 90° forud for den akustiske strømning ind i resonatoren. Der er tale om en mekanisk eller akustisk inerti.
Om resonansfrekvensen (vi taler stadig om skitsen ovenfor) kan amplituden være stor for en meget lille kraft. Ved resonans er impedansen altså meget lav, set ud fra den kraft, der påføres massen udefra (skemaet ovenfor). Ved resonans er der maksimal strøm ind og ud af resonatoren.
Se nu på, hvad der sker, hvis vi ser på trykket inde i resonatoren (væk fra halsen). Her ser vi på kraften på fjederen, så vores mekaniske analogi ser ud som denne skematiske fremstilling.
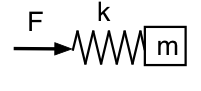
Denne gang betyder lav frekvens, at kraften kan være lille for en given amplitude: fjederen og massen bevæger sig sammen som en masse, og systemet ser denne gang inertivt ud ved lav frekvens. Ved høj frekvens bevæger massen sig næsten ikke, og systemet er fjederlignende eller eftergiveligt. Faseforholdene er således modsat af det, vi havde før: ved lav f er p 90° foran U; ved høj f er p 90° bagud i forhold til U.
Komplikationer, der involverer den effektive længde
Det første diagram på denne side tegner “proppen” af luft, som om den var en cylinder, der ender pænt i hver ende af flaskehalsen. Dette er for forenklet. I praksis bevæger der sig et ekstra volumen både indvendigt og udvendigt med luften i halsen – som antydet i animationen ovenfor. Den ekstra længde, der skal lægges til halsens geometriske længde, er typisk (og meget omtrentligt) på 0,6 gange radius i den udvendige ende og en radius i den indvendige ende).
|
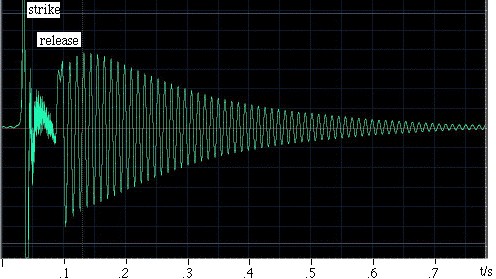
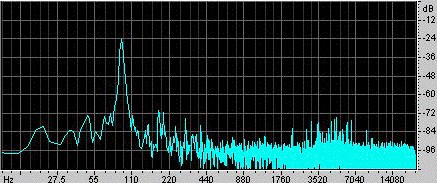
Et eksempel. Ra Inta har lavet dette eksempel. Han tog en sfærisk Helmholtz-resonator med et volumen på 0,00292 m3 og en cylindrisk hals med en længde på 0,080 m og et tværsnitsareal på 0,00083 m2. For at stimulere den slog han på den med håndfladen og slap den derefter. En mikrofon inde i resonatoren optager lyden, som er vist i oscillogrammet til venstre. Man kan se, at hånden forsegler resonatoren i noget mindre end 0,1 s, og at svingningerne i dette tidsrum er svagere og af relativt høj frekvens. Når hånden slippes, etableres der en svingning, som gradvist dør ud, efterhånden som den mister energi gennem viskose og turbulente træk og også ved lydstråling. En nærmere undersøgelse viser, at frekvensen stiger en smule, når hånden bevæger sig væk fra den åbne ende, fordi denne hånden begrænser den faste vinkel, der er tilgængelig for stråling, og dermed øger endeeffekten (eller endekorrektionen). Halsens længde forøges med en afskærmet og en uafskærmet endeeffekt, hvilket giver den en effektiv længde på 0,105 m. Med en lydhastighed på 343 m/s giver ovenstående udtryk en resonansfrekvens på 90 Hz. |
|
Helmholtz-resonanser og guitarer
* Jeg sagde ovenfor, at luften i en guitarkrop næsten virker som en Helmholtz-oscillator. Dette tilfælde er kompliceret, fordi kroppen kan svulme lidt op, når lufttrykket stiger indeni – og også fordi luften “i” guitarens lydhul har en geometri, der er mindre let at visualisere end den i en flaskehals. I tilfældet med guitarens krop er længden af luftens prop nemlig omtrent lig med de to “endeeffekter” i enden af et “rør”, som kun er et par mm tykt. Slutvirkningerne er imidlertid relateret til og af samme størrelse som hullets radius, så luftmassen er betydelig. Længden af endeeffekten af et cylindrisk rør, der munder ud i en uendelig, plan baffel, er 0,85 gange rørets radius. Selv om klangbunden på en guitar ikke er uendelig, kan man forvente en lignende endeeffekt, og derfor vil den effektive længde af “proppen” af luft være ca. 1,7 gange hullets radius. (Nogle fabrikanter øger dette ved at fastgøre et kort rør under lydhullet, med samme radius).
Et par personer har skrevet og spurgt, hvor stort lydhullet skal være for et givet instrument. Nå, men vi kan bruge ligningen ovenfor til at begynde at besvare dette spørgsmål. Kroppens hævelse er dog vigtig. Det gør luftens “fjeder” noget blødere og sænker dermed frekvensen. Den rene Helmholtz-resonans kan undersøges ved at holde volumenet af kroppen konstant. Når man måler dette, er det en almindelig praksis at begrave guitaren i sand for at forhindre kroppens hævelse eller “vejrtrækning”. Der spilles dog normalt ikke på guitarer i denne situation. Helmholtz-beregningen vil derfor give en overvurdering af resonansfrekvensen for en rigtig, fleksibel krop.
Lad os antage et cirkulært lydhul med radius r, så S = πr2, og L = 1,7r som forklaret ovenfor. Når vi substituerer i ligningen for Helmholtz-frekvensen ved hjælp af c = 340 m/s, får vi:
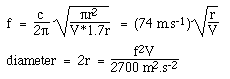
Bemærk, at vi bruger standard SI-enheder: Vi har brugt lydhastigheden i meter og sekunder, så volumenet skal være i kubikmeter og frekvensen i Hertz for at give et svar i meter.
Det er mere kompliceret, når tonehullerne ikke er cirkulære, fordi den endelige effekt ikke er lig med den, som en cirkel med samme areal giver. Ph.d.-studerende og luthier John McLennan er ved at skrive en rapport med nogle målinger om dette, som vi snart vil lægge ud her.
På instrumenter i guitar- og violinfamilien er Helmholtz-resonansen (plus krop) ofte tæt på eller lidt under frekvensen for den næstlaveste streng, omkring D på en violin eller G-A på en guitar. Du kan reducere eller forskyde Helmholtz-frekvensen betydeligt ved at dække hele eller en del af hullet med et passende formet stykke stift karton. Hvis du så spiller en tone i nærheden af resonansen og derefter skubber kortet, så det skiftevis dækker og afslører hullet, vil du tydeligt kunne høre resonansens effekt.
Er den 0,85r-effekt rimelig? Ra Inta, der har lavet en ph.d. om guitarakustik i vores laboratorium, foreslår en interessant demonstration:
Dæmp strengene på din guitar, så de ikke vibrerer (f.eks. et lommetørklæde mellem strengene og gribebrættet). Hold den ene hånds håndflade over lydhullet og tæt på det. Med en finger fra din anden hånd slår du et skarpt slag på klangbunden nær klanghullet og tæt på 1. streng. Du vil mærke en luftpuls på din håndflade. Slaget med fingeren skubber klangbunden indad og presser noget luft ud af kroppen. Flyt nu din hånd gradvist længere væk fra hullet, og fortsæt med at banke med fingeren. Hvornår holder du op med at mærke luftbevægelsen? Dette vil give dig et groft skøn over længden af “endeeffekten” i tilfælde af klanghullet.
Tuning the Helmholtz resonance
Blandt publikationerne fra John McLennan, der er ph.d.-studerende i dette laboratorium, er der en artikel, hvori han varierer Helmholtz-resonansen ved at variere lydens hastighed.
- McLennan, J.E. (2003) “A0 and A1 studies on the violin using CO2, He, and air/helium mixtures.” Acustica, 89, 176-180.
Nogle billeder af historiske Helmholtz-resonatorer stillet til rådighed af Thomas B. Greenslade, Kenyon College, Ohio.
Leave a Reply