Green’s funktion

Generelt set, er en grøn funktion en integral kerne, der kan bruges til at løse differentialligninger fra et stort antal familier, herunder enklere eksempler såsom ordinære differentialligninger med begyndelses- eller randværdibetingelser, samt vanskeligere eksempler såsom inhomogene partielle differentialligninger (PDE) med randbetingelser. Green’s funktioner er vigtige af en række årsager og giver mulighed for visuelle fortolkninger af de handlinger, der er forbundet med en kraftkilde eller en ladning koncentreret i et punkt (Qin 2014), hvilket gør dem særligt nyttige inden for områder af anvendt matematik. Navnlig anvendes Green’s funktionsmetoder i vid udstrækning i f.eks, fysik og ingeniørvidenskab.

Mere præcist, givet en lineær differentieloperator , der virker på samlingen af fordelinger over en delmængde af et vist euklidisk rum , er en Green-funktion i punktet svarende til er en hvilken som helst løsning af

(1)

hvor betegner deltafunktionen. Motivationen for at definere en sådan funktion er vidt udbredt, men ved at multiplicere ovenstående identitet med en funktion og integrere med hensyn til fås

(2)

Den højre side reduceres blot til på grund af egenskaber ved deltafunktionen, og fordi er en lineær operatør, der kun virker på og ikke på , kan venstre side omskrives som

(3)

Denne reduktion er især nyttig, når man skal løse for i differentialligninger af formen

(4)

hvor ovenstående aritmetik bekræfter, at

(5)

og hvorved det følger, at har den specifikke integralform

(6)

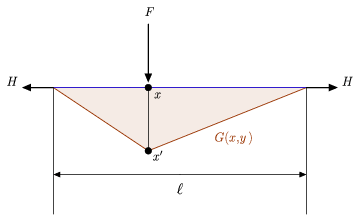
Figuren ovenfor illustrerer både den intuitive fysiske fortolkning af en grøn funktion samt en relativt simpel tilhørende differentialligning, som man kan sammenligne ovenstående definition med (Hartmann 2013). Den viser især et stramt reb af længde , der er ophængt mellem to vægge, og som holdes på plads af en identisk horisontal kraft , der påføres i hver af dets ender, og en sidelast , der er placeret i et indre punkt på rebet. Lad være det punkt, der svarer til på det afbøjede reb, antag, at den nedadgående kraft er konstant, lad os sige , og lad betegne rebets afbøjning. Svarende til dette fysiske system er differentialligningen

(7)

for med , et system, hvis enkelhed gør det muligt at skrive både dets løsning og dets Green’s funktion eksplicit:

(8)

og

(9)

hvortil hhv. Som det fremgår af ovenstående figur, har det forskudte reb det stykkevis lineære format givet ved ovenfor, hvilket bekræfter påstanden om, at Green’s funktion , der er knyttet til dette system, repræsenterer virkningen af det vandrette reb svarende til påføring af en kraft .

En Green’s funktion, der tager et par argumenter , kaldes undertiden en to-punkts Green’s funktion. Dette står i modsætning til flerpunkts-Green’s-funktioner, som er af særlig betydning inden for mange-krops-teori.

Som et elementært eksempel på en topunktsfunktion som defineret ovenfor kan man overveje problemet med at bestemme potentialet , der genereres af en ladningsfordeling, hvis ladningstæthed er , hvorved anvendelse af Poissons ligning og Coulombs lov på potentialet ved produceret af hvert element med ladning giver en løsning

(10)

hvilket gælder, under visse betingelser, over det område, hvor . Da højre side kan ses som en integraloperator, der omdanner til , kan man omskrive denne løsning i form af en Green’s funktion , der har formen

(11)

hvorved løsningen kan omskrives:

(12)

(Arfken 2012).

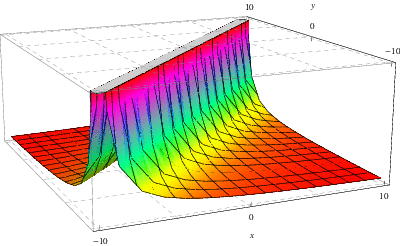
Overstående figur viser den grønne funktion, der er knyttet til løsningen af –ligningen, der er diskuteret ovenfor, hvor her, og , henholdsvis , er plottet på -, henholdsvis -, aksen.

En noget omfattende liste over Green’s funktioner svarende til forskellige differentialligninger vedligeholdes online af Kevin Cole (Cole 2000).

På grund af den mangfoldighed af litteratur, der er skrevet om Green’s funktioner, kan der opstå flere forskellige notationer og definitioner, hvoraf nogle er aktuelt anderledes end ovenstående, men som generelt ikke påvirker de vigtige egenskaber ved resultaterne. Som ovenstående eksempel illustrerer, foretrækker nogle forfattere f.eks. at betegne variablerne og med vektorer og for at understrege, at de er elementer af for nogle , som kan være større end 1 (Arfken 1985). Det er også relativt almindeligt at se definitionen med negativt fortegn, således at er defineret som den funktion, for hvilken

(13)

men på grund af at denne rent fysiske betragtning ikke har nogen indflydelse på den underliggende matematik, overses dette synspunkt generelt. Der kendes også flere andre notationer for en Green’s funktion, hvoraf nogle omfatter brugen af en lille i stedet for (Stakgold 1979) samt medtagelsen af en lodret streg i stedet for et komma, f.eks, (Duffy 2001).

I andre tilfælde præsenterer litteraturen definitioner, som er tæt forbundet med de kontekster, hvori de præsenteres. F.eks. definerer nogle forfattere Green’s funktioner som funktioner, der opfylder et bestemt sæt af betingelser, f.eks. eksistens på en særlig slags domæne, tilknytning til en meget speciel differentiel operatør eller opfyldelse af et præcist sæt randbetingelser. Et af de mest almindelige sådanne eksempler kan findes i noter af f.eks, Speck, hvor en grøn funktion er defineret til at opfylde for punkter og for alle punkter , der ligger i grænsen af (Speck 2011). Denne særlige definition præsenterer en integralkernel, der svarer til løsningen af en generaliseret Poisson-ligning, og ville derfor støde på åbenlyse begrænsninger, når den tilpasses til en mere generel indstilling. På den anden side er sådanne eksempler ikke uden deres fordele. I tilfældet med det generaliserede Poisson-eksempel ovenfor kan f.eks. hver sådan Green’s funktion opdeles således, at

(14)

hvor og for den regelmæssige laplacian (Hartman 2013). I sådanne situationer er kendt som den fundamentale løsning af den underliggende differentialligning, og er kendt som dens regulære løsning; som sådan kaldes og undertiden for henholdsvis den fundamentale og den regulære del af .

Flere grundlæggende egenskaber ved en generel Green’s funktion følger umiddelbart (eller næsten) af dens definition og overføres til alle særlige tilfælde. For eksempel, hvis kernen af operatøren er ikke-triviel, kan der være flere Green’s funktioner tilknyttet en enkelt operatør; som følge heraf skal man udvise forsigtighed, når man henviser til “den” Green’s funktion. Green’s funktioner opfylder en adjungeret symmetri i deres to argumenter, således at

(15)

hvor her er defineret som løsningen af ligningen

(16)

Her er adjunkten til . En umiddelbar følge af denne kendsgerning er, at for selvadjointoperatorer er symmetrisk:

(17)

Denne identitet kaldes ofte reciprocitetsprincippet og siger i fysiske termer, at responsen ved forårsaget af en enhedskilde ved er den samme som responsen ved forårsaget af en enhedskraft ved (Stakgold 1979).

Den væsentlige egenskab ved enhver grøn funktion er, at den giver en måde at beskrive responsen af en vilkårlig differentialligningsløsning på en eller anden form for kildeterm i tilstedeværelsen af et vist antal randbetingelser (Arfken et al. 2012). Nogle forfattere mener, at en Green’s funktion tjener nogenlunde en analog rolle i teorien om partielle differentialligninger som Fourier-serier i løsningen af almindelige differentialligninger (Mikula og Kos 2006).

For mere abstrakte scenarier findes der en række begreber, der tjener som kontekstspecifikke analoger til begrebet Green’s funktion. Inden for f.eks. funktionel analyse er det ofte nyttigt at overveje en såkaldt generaliseret Green’s funktion, som har mange analoge egenskaber, når den integreres abstrakt mod funktionaler i stedet for funktioner. Sådanne generaliseringer har faktisk givet en helt analog gren af den teoretiske PDE-analyse og er i sig selv genstand for en stor mængde forskning.