Gram-Schmidt-processen
af Marco Taboga, PhD
Gram-Schmidt-processen (eller -proceduren) er en række operationer, der gør det muligt at omdanne et sæt af lineært uafhængige vektorer til et sæt ortonormale vektorer, der dækker det samme rum som det oprindelige sæt.

Preliminarier
Lad os gennemgå nogle begreber, der er væsentlige for at forstå Gram-Schmidt-processen.
Husk, at to vektorer  og
og  siges at være ortogonale, hvis og kun hvis deres indre produkt er lig nul, det vil sige,
siges at være ortogonale, hvis og kun hvis deres indre produkt er lig nul, det vil sige,
Givet et indre produkt kan vi definere normen (længden) for en vektor  som følger:
som følger:
Et sæt af vektorer kaldes ortonormalt, hvis og kun hvis dets elementer har enhedsnorm og er ortogonale til hinanden. Med andre ord er et sæt af  vektorer
vektorer  ortonormalt, hvis og kun hvis
ortonormalt, hvis og kun hvis
Vi har bevist, at vektorerne i et ortonormalt sæt er lineært uafhængige.
Når en basis for et vektorrum også er et ortonormalt sæt, kaldes det en ortonormal basis.
Projektioner på ortonormale sæt
I Gram-Schmidt-processen anvender vi gentagne gange den næste sætning, som viser, at enhver vektor kan nedbrydes i to dele: 1) dens projektion på et ortonormalt sæt og 2) en rest, der er ortogonal til det givne ortonormale sæt.
Sætning Lad  være et vektorrum udstyret med et indre produkt
være et vektorrum udstyret med et indre produkt  . Lad
. Lad  være et ortonormalt sæt. For en hvilken som helst
være et ortonormalt sæt. For en hvilken som helst  har vi
har vi hvor
hvor  er ortogonal til
er ortogonal til  for en hvilken som helst
for en hvilken som helst 
Definere Så har vi for hver
Så har vi for hver  , at
, at hvor: i trin
hvor: i trin  og
og  har vi brugt den kendsgerning, at det indre produkt er lineært i sit første argument; i trin $rame{C}$ har vi anvendt det faktum, at
har vi brugt den kendsgerning, at det indre produkt er lineært i sit første argument; i trin $rame{C}$ har vi anvendt det faktum, at  hvis
hvis  , da vi har at gøre med et ortonormalt sæt; i trin
, da vi har at gøre med et ortonormalt sæt; i trin  har vi anvendt det faktum, at normen for
har vi anvendt det faktum, at normen for  er lig med 1. Derfor er
er lig med 1. Derfor er  , som defineret ovenfor, ortogonal til alle elementerne i det ortonormale sæt, hvilket beviser sætningen.
, som defineret ovenfor, ortogonal til alle elementerne i det ortonormale sæt, hvilket beviser sætningen.
Udtrykket kaldes den lineære projektion af
kaldes den lineære projektion af  på den ortonormale mængde
på den ortonormale mængde  , mens udtrykket
, mens udtrykket  kaldes residualen af den lineære projektion.
kaldes residualen af den lineære projektion.
Normalisering
En anden måske indlysende kendsgerning, som vi vil bruge gentagne gange i Gram-Schmidt-processen, er, at hvis vi tager en hvilken som helst vektor, der ikke er nul, og vi dividerer den med dens norm, så er resultatet af divisionen en ny vektor, der har enhedsnorm.
Med andre ord, hvis  så har vi ved normens definitionsegenskab, at
så har vi ved normens definitionsegenskab, at 
Som følge heraf kan vi definere og ved normens positivitet og absolut homogenitet, har vi
og ved normens positivitet og absolut homogenitet, har vi
Overblik over proceduren
Nu hvor vi ved, hvordan man normaliserer en vektor, og hvordan man dekomponerer den i en projektion på et ortonormalt sæt og en rest, er vi klar til at forklare Gram-Schmidt-proceduren.
Vi vil give et overblik over fremgangsmåden, hvorefter vi vil udtrykke den formelt som en sætning, og vi vil diskutere alle de tekniske detaljer i beviset for sætningen.
Her er overblikket.
Vi får et sæt af lineært uafhængige vektorer  .
.
For at starte processen normaliserer vi den første vektor, dvs. vi definerer
I det andet trin projicerer vi  på
på  :
: hvor
hvor  er restværdien af projektionen.
er restværdien af projektionen.
Derefter normaliserer vi residualet:
Vi vil senere bevise, at  (således at normaliseringen kan foretages), fordi startvektorerne er lineært uafhængige.
(således at normaliseringen kan foretages), fordi startvektorerne er lineært uafhængige.
De to vektorer  og
og  , der således opnås, er ortonormale.
, der således opnås, er ortonormale.
I det tredje trin projicerer vi  på
på  og
og  :
: og vi beregner restværdien af projektionen
og vi beregner restværdien af projektionen  .
.
Vi normaliserer den derefter:
Vi fortsætter på denne måde, indtil vi får den sidste normaliserede residual  .
.
Ved processens afslutning danner vektorerne  et ortonormalt sæt, fordi:
et ortonormalt sæt, fordi:
-
de er resultatet af en normalisering, og som følge heraf har enhedsnorm;
-
hver
 fås fra en residual, der har den egenskab at være ortogonal til
fås fra en residual, der har den egenskab at være ortogonal til  .
.
For at supplere denne oversigt skal vi huske, at det lineære spænd af  er mængden af alle vektorer, der kan skrives som lineære kombinationer af
er mængden af alle vektorer, der kan skrives som lineære kombinationer af  ; det betegnes med
; det betegnes med og det er et lineært rum.
og det er et lineært rum.
Da vektorerne  er lineært uafhængige kombinationer af
er lineært uafhængige kombinationer af  , kan enhver vektor, der kan skrives som en lineær kombination af
, kan enhver vektor, der kan skrives som en lineær kombination af  , også skrives som en lineær kombination af
, også skrives som en lineær kombination af  . Derfor er spændvidderne for de to sæt af vektorer sammenfaldende:
. Derfor er spændvidderne for de to sæt af vektorer sammenfaldende:
Formelt udsagn
Vi formaliserer her Gram-Schmidt-processen som et udsagn, hvis bevis indeholder alle de tekniske detaljer i proceduren.
Sætning Lad  være et vektorrum udstyret med et indre produkt
være et vektorrum udstyret med et indre produkt  . Lad
. Lad  være lineært uafhængige vektorer. Så findes der et sæt ortonormale vektorer
være lineært uafhængige vektorer. Så findes der et sæt ortonormale vektorer  , således at
, således at for enhver
for enhver  .
.
Beviset er ved induktion: Først beviser vi, at sætningen er sand for  , og derefter beviser vi, at den er sand for en generisk
, og derefter beviser vi, at den er sand for en generisk  , hvis den gælder for
, hvis den gælder for  . Når
. Når  , har vektoren
, har vektoren enhedsnorm, og den udgør i sig selv et ortonormalt sæt: der er ingen andre vektorer, så ortogonalitetsbetingelsen er trivielt opfyldt. Mængden
enhedsnorm, og den udgør i sig selv et ortonormalt sæt: der er ingen andre vektorer, så ortogonalitetsbetingelsen er trivielt opfyldt. Mængden er mængden af alle skalariske multipla af
er mængden af alle skalariske multipla af  , som også er skalariske multipla af
, som også er skalariske multipla af  (og vice versa). Derfor:
(og vice versa). Derfor:  Nu antager vi, at sætningen er sand for
Nu antager vi, at sætningen er sand for  . Så kan vi projicere
. Så kan vi projicere  på
på  :
: hvor residualen
hvor residualen  er ortogonal til
er ortogonal til  . Antag, at $arepsilon _{k}=0$. Så,
. Antag, at $arepsilon _{k}=0$. Så, da vi ved en antagelse har
da vi ved en antagelse har  for enhver
for enhver  , har vi, at
, har vi, at  for enhver
for enhver  , hvor
, hvor  er skalarer. Derfor,
er skalarer. Derfor, Med andre ord fører antagelsen om, at $arepsilon _{k}=0$ til den konklusion, at $s_{k}$ er en lineær kombination af
Med andre ord fører antagelsen om, at $arepsilon _{k}=0$ til den konklusion, at $s_{k}$ er en lineær kombination af  . Men det er umuligt, fordi en af antagelserne i sætningen er, at
. Men det er umuligt, fordi en af antagelserne i sætningen er, at  er lineært uafhængige. Som følge heraf må det være sådan, at
er lineært uafhængige. Som følge heraf må det være sådan, at  . Vi kan derfor normalisere residualet og definere vektoren
. Vi kan derfor normalisere residualet og definere vektoren som har enhedsnorm. Vi ved allerede, at
som har enhedsnorm. Vi ved allerede, at  er ortogonal til
er ortogonal til  . Dette indebærer, at også
. Dette indebærer, at også  er ortogonal til
er ortogonal til  . Således er
. Således er  et ortonormalt sæt. Tag nu en hvilken som helst vektor
et ortonormalt sæt. Tag nu en hvilken som helst vektor  , der kan skrives som
, der kan skrives som hvor
hvor  er skalarer. Da vi ved en antagelse
er skalarer. Da vi ved en antagelse  har vi, at ligning (2) også kan skrives som
har vi, at ligning (2) også kan skrives som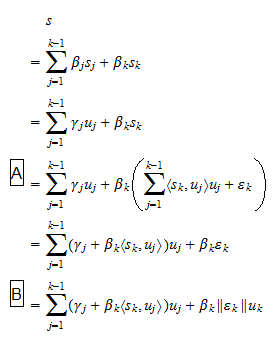 hvor
hvor  er skalarer, og: i trin
er skalarer, og: i trin  har vi brugt ligning (1); i trin
har vi brugt ligning (1); i trin  har vi brugt definitionen af
har vi brugt definitionen af  . Vi har således bevist, at enhver vektor, der kan skrives som en lineær kombination af
. Vi har således bevist, at enhver vektor, der kan skrives som en lineær kombination af  , også kan skrives som en lineær kombination af
, også kan skrives som en lineær kombination af  . Antagelse (3) gør det muligt at bevise det omvendte på en helt analog måde:
. Antagelse (3) gør det muligt at bevise det omvendte på en helt analog måde: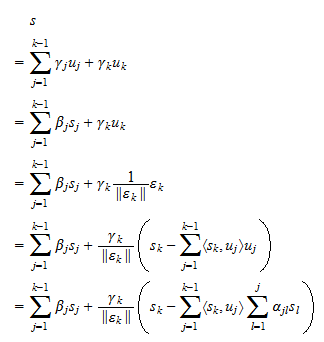 Med andre ord er enhver lineær kombination af
Med andre ord er enhver lineær kombination af  også en lineær kombination af
også en lineær kombination af  . Dette beviser, at
. Dette beviser, at  og afslutter beviset.
og afslutter beviset.
Hvert indre produktrum har en ortonormal basis
Følgende sætning præsenterer en vigtig konsekvens af Gram-Schmidt-processen.
Sætning Lad  være et vektorrum udstyret med et indre produkt
være et vektorrum udstyret med et indre produkt  . Hvis
. Hvis  har finite dimension
har finite dimension  , findes der en ortonormal basis
, findes der en ortonormal basis  for
for  .
.
Da  har finite dimensioner, findes der mindst én basis for
har finite dimensioner, findes der mindst én basis for  , som består af
, som består af  vektorer
vektorer  . Vi kan anvende Gram-Schmidt-proceduren på grundlaget og opnå et ortonormalt sæt
. Vi kan anvende Gram-Schmidt-proceduren på grundlaget og opnå et ortonormalt sæt  . Da
. Da  er en basis, spænder den over
er en basis, spænder den over  . Derfor er
. Derfor er 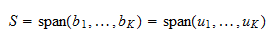 Dermed er
Dermed er  en ortonormal basis for
en ortonormal basis for  .
.
Løste opgaver
Nedenfor finder du nogle opgaver med forklarede løsninger.
Ovelse 1
Betragt rummet  af alle
af alle  vektorer med reelle indgange og det indre produkt
vektorer med reelle indgange og det indre produkt hvor
hvor  og
og  er transponeringen af
er transponeringen af  . Definer vektoren
. Definer vektoren
Normalisér  .
.
Normen for  er
er Derfor, normaliseringen af
Derfor, normaliseringen af  er
er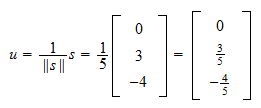
Ovelse 2
Betragt rummet  af alle
af alle  vektorer med reelle poster og det indre produkt
vektorer med reelle poster og det indre produkt hvor
hvor  . Betragt de to lineært uafhængige vektorer
. Betragt de to lineært uafhængige vektorer
Transformér dem til et ortonormalt sæt ved hjælp af Gram-Schmidt-processen.
Normen for  er
er  Derfor, den første ortonormale vektor er
Derfor, den første ortonormale vektor er Det indre produkt af
Det indre produkt af  og
og  er
er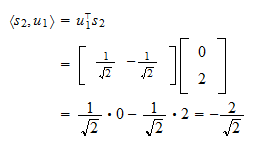 Projektionen af
Projektionen af  på
på  er
er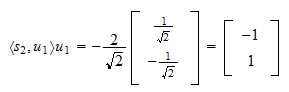 Restproduktet af projektionen er
Restproduktet af projektionen er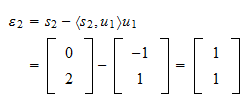 Restproduktets norm er
Restproduktets norm er og det normaliserede restprodukt er
og det normaliserede restprodukt er Dermed er, det ortonormale sæt, som vi ledte efter, er
Dermed er, det ortonormale sæt, som vi ledte efter, er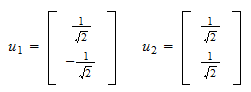
Hvordan citeres
Citer venligst som:
Taboga, Marco (2017). “Gram-Schmidt-processen”, Lectures on matrix algebra. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.
Leave a Reply