Gibbs Sampling

Som andre MCMC-metoder, konstruerer Gibbs sampler en Markov-kæde, hvis værdier konvergerer mod en målfordeling. Gibbs Sampling er faktisk et særligt tilfælde af Metropolis-Hastings-algoritmen, hvor forslag altid accepteres.

For at uddybe dette, lad os antage, at du ønsker at prøve en multivariat sandsynlighedsfordeling.

Bemærkning: En multivariat sandsynlighedsfordeling er en funktion af flere variabler (dvs. 2-dimensionel normalfordeling).

Vi ved ikke, hvordan vi kan udtage stikprøver direkte fra sidstnævnte. Men på grund af en eller anden matematisk bekvemmelighed eller måske bare rent held kender vi tilfældigvis de betingede sandsynligheder.

Det er her Gibbs sampling kommer ind i billedet. Gibbs Sampling kan anvendes, når den fælles fordeling ikke kendes eksplicit eller er vanskelig at udtage direkte prøver fra, men den betingede fordeling af hver enkelt variabel er kendt og er lettere at udtage prøver fra.

Vi starter med at vælge en indledende værdi for de tilfældige variabler X & Y. Derefter udtager vi prøver fra den betingede sandsynlighedsfordeling for X givet Y = Y⁰ betegnet p(X|Y⁰). I det næste trin udtager vi en ny værdi af Y betinget af X¹, som vi netop har beregnet. Vi gentager proceduren i yderligere n – 1 gentagelser, idet vi skiftevis trækker en ny prøve fra den betingede sandsynlighedsfordeling for X og den betingede sandsynlighedsfordeling for Y, givet den aktuelle værdi af den anden tilfældige variabel.

Lad os se på et eksempel. Lad os antage, at vi havde følgende posteriore og betingede sandsynlighedsfordelinger.

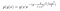
hvor g(y) indeholder de termer, der ikke omfatter x, og g(x) indeholder dem, der ikke afhænger af y.

Vi kender ikke værdien af C (normaliseringskonstant). Vi kender dog de betingede sandsynlighedsfordelinger. Derfor kan vi bruge Gibbs Sampling til at tilnærme os den efterfølgende fordeling.

Bemærk: De betingede sandsynligheder er faktisk normalfordelinger og kan omskrives som følger:

I betragtning af de foregående ligninger går vi videre til at implementere Gibbs Sampling-algoritmen i Python. Til at begynde med importerer vi følgende biblioteker.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

Vi definerer funktionen for den efterfølgende fordeling (antag C=1).

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

Dernæst plotter vi sandsynlighedsfordelingen.

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Nu vil vi forsøge at estimere sandsynlighedsfordelingen ved hjælp af Gibbs Sampling. Som vi tidligere har nævnt, er de betingede sandsynligheder normalfordelinger. Derfor kan vi udtrykke dem i form af mu og sigma.

I den følgende kodeblok definerer vi funktioner for mu og sigma, initialiserer vores tilfældige variabler X & Y og indstiller N (antallet af iterationer).

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

Vi gennemgår Gibbs Sampling-algoritmen.

for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x

Slutteligt plotter vi resultaterne.

plt.hist(x, bins=50);
plt.hist(y, bins=50);

plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

Som vi kan se, at den sandsynlighedsfordeling, der er opnået ved hjælp af Gibbs Sampling-algoritmen, er en god tilnærmelse af målfordelingen.

Slutning

Gibbs Sampling er en Monte Carlo Markov Chain-metode, der iterativt trækker en instans fra fordelingen af hver variabel, betinget af de aktuelle værdier af de andre variabler, med henblik på at estimere komplekse fælles fordelinger. I modsætning til Metropolis-Hastings-algoritmen accepterer vi altid forslaget. Gibbs Sampling kan således være langt mere effektiv.