Friedman-test i SPSS Statistics
SPSS Statistics
SPSS Statistics Output for Friedman-testen
SPSS Statistics genererer enten to eller tre tabeller, afhængigt af om du har valgt at få genereret beskrivelser og/eller kvartiler ud over at køre Friedman-testen.
Descriptive Statistics Table
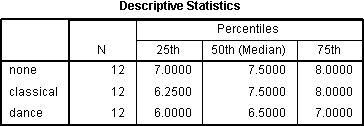
Tabellen Descriptives Statistics produceres, hvis du har valgt indstillingen Quartiles:
Publiceret med skriftlig tilladelse fra SPSS Statistics, IBM Corporation.
Dette er en meget nyttig tabel, fordi den kan bruges til at præsentere beskrivende statistik i dit resultatafsnit for hvert af tidspunkterne eller betingelserne (afhængigt af dit undersøgelsesdesign) for din afhængige variabel. Denne anvendelighed vil blive præsenteret i afsnittet “Rapportering af output” senere.
Rangtabel
Rangtabellen viser den gennemsnitlige rang for hver af de relaterede grupper, som vist nedenfor:

Publiceret med skriftlig tilladelse fra SPSS Statistics, IBM Corporation.
Friedman-testen sammenligner de gennemsnitlige rangeringsgrader mellem de relaterede grupper og angiver, hvordan grupperne adskiller sig fra hinanden, og den er medtaget af denne grund. Det er dog ikke særlig sandsynligt, at du rent faktisk vil rapportere disse værdier i dit resultatafsnit, men sandsynligvis vil du rapportere medianværdien for hver relateret gruppe.
Teststatistiktabel
Teststatistiktabellen informerer dig om det faktiske resultat af Friedman-testen, og om der var en generel statistisk signifikant forskel mellem gennemsnitsrækkerne for dine relaterede grupper. For det eksempel, der er anvendt i denne vejledning, ser tabellen således ud:

Publiceret med skriftlig tilladelse fra SPSS Statistics, IBM Corporation.
Tabellen ovenfor viser teststatistikværdien (χ2) (“Chi-square”), frihedsgrader (“df”) og signifikansniveauet (“Asymp. Sig.”), hvilket er alt, hvad vi har brug for for at rapportere resultatet af Friedman-testen. Ud fra vores eksempel kan vi se, at der er en generel statistisk signifikant forskel mellem de relaterede gruppers gennemsnitsranger. Det er vigtigt at bemærke, at Friedman-testen er en omnibus-test, ligesom dens parametriske alternativ; det vil sige, at den fortæller dig, om der er overordnede forskelle, men den udpeger ikke præcist, hvilke grupper der specifikt adskiller sig fra hinanden. For at gøre dette er du nødt til at udføre post hoc-tests, hvilket vil blive diskuteret efter næste afsnit.
SPSS Statistics
Rapportering af resultatet af Friedman-testen (uden post hoc-test)
Du kan rapportere resultatet af Friedman-testen på følgende måde:
- Almen
Der var en statistisk signifikant forskel i opfattet anstrengelse afhængigt af, hvilken type musik der blev lyttet til under løb, χ2(2) = 7.600, p = 0,022.
Du kunne også medtage medianværdierne for hver af de relaterede grupper. På dette tidspunkt ved du dog kun, at der er forskelle et eller andet sted mellem de beslægtede grupper, men du ved ikke præcis, hvor disse forskelle ligger. Husk dog, at hvis resultatet af din Friedman-test ikke var statistisk signifikant, bør du ikke køre post hoc-tests.
Post hoc-tests
For at undersøge, hvor forskellene faktisk forekommer, skal du køre separate Wilcoxon signed-rank-tests på de forskellige kombinationer af beslægtede grupper. I dette eksempel ville du altså sammenligne følgende kombinationer:
- Ingen til klassisk.
- Ingen til dans.
- Klassisk til dans.
Du skal bruge en Bonferroni-justering på de resultater, du får fra Wilcoxon-testene, fordi du foretager flere sammenligninger, hvilket gør det mere sandsynligt, at du vil erklære et resultat for signifikant, når du ikke burde (en type I-fejl). Heldigvis er Bonferroni-justeringen meget nem at beregne; du skal blot tage det signifikansniveau, du oprindeligt brugte (i dette tilfælde 0,05), og dividere det med det antal test, du udfører. Så i dette eksempel har vi et nyt signifikansniveau på 0,05/3 = 0,017. Det betyder, at hvis p-værdien er større end 0,017, har vi ikke et statistisk signifikant resultat.
Kører du disse test (se hvordan med vores vejledning om Wilcoxon signed-rank test) på resultaterne fra dette eksempel, får du følgende resultat:

Publiceret med skriftlig tilladelse fra SPSS Statistics, IBM Corporation.
Denne tabel viser resultatet af Wilcoxon signed-rank-testen for hver af vores kombinationer. Det er vigtigt at bemærke, at signifikansværdierne ikke er blevet justeret i SPSS Statistics for at kompensere for flere sammenligninger – du skal manuelt sammenligne de signifikansværdier, der produceres af SPSS Statistics, med det Bonferroni-justerede signifikansniveau, som du har beregnet. Vi kan se, at ved p < 0,017 signifikansniveauet var det kun den opfattede anstrengelse mellem ingen musik og dans (dance-none, p = 0,008), der var statistisk signifikant forskellig.
SPSS Statistics
Rapportering af resultatet af Friedman-testen (med post hoc-test)
Du kan rapportere resultaterne af Friedman-testen med post hoc-test på følgende måde:
- Almen
Der var en statistisk signifikant forskel i opfattet anstrengelse afhængigt af, hvilken type musik der blev lyttet til under løb, χ2(2) = 7.600, p = 0.022. Post hoc-analyse med Wilcoxon signed-rank-test blev udført med en Bonferroni-korrektion anvendt, hvilket resulterede i et signifikansniveau fastsat til p < 0,017. Medianen (IQR) af de opfattede anstrengelsesniveauer for løbeforsøget uden musik, klassisk og dansemusik var henholdsvis 7,5 (7 til 8), 7,5 (6,25 til 8) og 6,5 (6 til 7). Der var ingen signifikante forskelle mellem løbeforsøgene uden musik og løb med klassisk musik (Z = -0,061, p = 0,952) eller mellem løbeforsøgene med klassisk og dansemusik (Z = -1,811, p = 0,070), på trods af en generel reduktion i den opfattede anstrengelse i løbeforsøgene med dansemusik i forhold til klassisk løb. Der var dog en statistisk signifikant reduktion i den opfattede anstrengelse i forsøget med dansemusik vs. ingen musik (Z = -2,636, p = 0,008).
Leave a Reply