En let introduktion til det konvekse skrogproblem

Konvekse skrog har tendens til at være nyttige på mange forskellige områder, nogle gange helt uventet. I denne artikel vil jeg forklare den grundlæggende idé om 2d konvekse skrog, og hvordan man kan bruge graham-scanningen til at finde dem. Så hvis du allerede kender til graham scanningen, er denne artikel ikke for dig, men hvis ikke, skulle dette gøre dig fortrolig med nogle af de relevante begreber.

Den konvekse skrog af et sæt af punkter er defineret som den mindste konvekse polygon, der omslutter alle punkterne i sættet. Konveks betyder, at polygonen ikke har noget hjørne, der er bøjet indad.

De røde kanter på den højre polygon omslutter det hjørne, hvor formen er konkav, det modsatte af konveks.

En nyttig måde at tænke på det konvekse skrog på er gummibåndsanalogien. Lad os antage, at punkterne i mængden var søm, der stak ud af en flad overflade. Forestil dig nu, hvad der ville ske, hvis du tog et elastikbånd og spændte det rundt om sømmene. Ved at forsøge at trække sig sammen igen til sin oprindelige længde ville elastikken omslutte sømmene og berøre dem, der stikker længst ud fra midten.

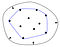
For at repræsentere det resulterende konvekse skrog i kode gemmer vi normalt listen af punkter, der holder dette elastikbånd op, dvs. listen af punkter på det konvekse skrog.

Bemærk, at vi stadig skal definere, hvad der skal ske, hvis tre punkter ligger på samme linje. Hvis man forestiller sig, at gummibåndet har et punkt, hvor det rører et af sømmene, men slet ikke bøjer der, betyder det, at det søm der ligger på en lige linje mellem to andre søm. Afhængigt af problemet kan vi måske betragte dette søm langs den lige linje som en del af udgangen, da det rører gummibåndet. På den anden side kan vi også sige, at dette søm ikke bør være en del af resultatet, fordi gummibåndets form ikke ændrer sig, når vi fjerner det. Denne beslutning afhænger af det problem, du arbejder med i øjeblikket, og bedst af alt, hvis du har et input, hvor ingen tre punkter er kollineære (det er ofte tilfældet i lette opgaver til programmeringskonkurrencer), så kan du endda helt ignorere dette problem.

Find det konvekse skrog

Hvis vi ser på et sæt punkter, kan vi med menneskelig intuition hurtigt finde ud af, hvilke punkter der sandsynligvis vil berøre det konvekse skrog, og hvilke der vil være tættere på centrum og dermed væk fra det konvekse skrog. Men det kræver lidt arbejde at omsætte denne intuition til kode.

For at finde det konvekse skrog af et sæt punkter kan vi bruge en algoritme kaldet Graham Scan, som anses for at være en af de første algoritmer inden for beregningsgeometri. Ved hjælp af denne algoritme kan vi finde den delmængde af punkter, der ligger på det konvekse skrog, sammen med den rækkefølge, som disse punkter mødes i, når vi går rundt om det konvekse skrog.

Algoritmen starter med at finde et punkt, som vi ved med sikkerhed ligger på det konvekse skrog. Punktet med den laveste y-koordinat kan f.eks. betragtes som et sikkert valg. Hvis der findes flere punkter på samme y-koordinat, tager vi det punkt, der har den største x-koordinat (dette fungerer også med andre hjørnepunkter, f.eks. først laveste x og derefter laveste y).

Dernæst sorterer vi de andre punkter efter den vinkel, de ligger i set fra startpunktet. Hvis to punkter tilfældigvis ligger i samme vinkel, skal det punkt, der ligger tættere på startpunktet, optræde tidligere i sorteringen.

Nu er idéen med algoritmen at gå rundt i dette sorterede array og for hvert punkt bestemme, om det ligger på det konvekse skrog eller ej. Det betyder, at vi for hver tripel af punkter, vi støder på, beslutter, om de danner et konvekst eller et konkavt hjørne. Hvis hjørnet er konkavt, så ved vi, at det midterste punkt ud af denne triplet ikke kan ligge på det konvekse skrog.

(Bemærk, at udtrykkene konkavt og konvekst hjørne skal bruges i forhold til hele polygonen, bare et hjørne i sig selv kan ikke være konvekst eller konkavt, da der ikke ville være nogen referenceretning.)

Vi gemmer de punkter, der ligger på det konvekse skrog, på en stak, på den måde kan vi tilføje punkter, hvis vi når dem på vores vej rundt om de sorterede punkter, og fjerne dem, hvis vi finder ud af, at de danner et konkavt hjørne.

(Strengt taget skal vi have adgang til de to øverste punkter i stakken, derfor bruger vi i stedet et std::vector, men vi tænker på det som en slags stak, fordi vi altid kun er interesseret i de øverste par elementer.)

Ved at gå rundt om den sorterede række af punkter tilføjer vi punktet til stakken, og hvis vi senere finder ud af, at punktet ikke hører til det konvekse skrog, fjerner vi det.

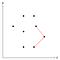
Vi kan måle, om det aktuelle hjørne bøjer indad eller udad ved at beregne krydsproduktet og kontrollere, om det er positivt eller negativt. Figuren ovenfor viser en triplet af punkter, hvor det hjørne, de danner, er konvekse, derfor forbliver det midterste af disse tre punkter på stakken indtil videre.

Går vi videre til det næste punkt, fortsætter vi med at gøre det samme: vi tjekker, om hjørnet er konvekst, og hvis ikke, fjerner vi punktet. Derefter fortsætter vi med at tilføje det næste punkt og gentager.

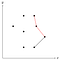
Dette hjørne markeret med rødt er konkavt, og derfor fjerner vi det midterste punkt fra stakken, da det ikke kan være en del af det konvekse skrog.

Hvordan ved vi, at dette giver os det rigtige svar?

At skrive et stringent bevis ligger uden for rammerne af denne artikel, men jeg kan skrive de grundlæggende idéer ned. Jeg opfordrer dig dog til at gå videre og forsøge at udfylde hullerne!

Da vi har beregnet krydsproduktet i hvert hjørne, ved vi med sikkerhed, at vi får en konveks polygon. Nu mangler vi blot at bevise, at denne konvekse polygon virkelig omslutter alle punkterne.

(Faktisk skal man også vise, at dette er den mindste mulige konvekse polygon, der opfylder disse betingelser, men det følger ret let af, at hjørnepunkterne i vores konvekse polygon er en delmængde af den oprindelige punktmængde.)

Sæt, der findes et punkt P uden for den polygon, vi lige har fundet.

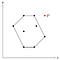
Da hvert punkt er blevet tilføjet til stakken én gang, ved vi, at P er blevet fjernet fra stakken på et eller andet tidspunkt. Det betyder, at P sammen med sine nabopunkter, lad os kalde dem O og Q, dannede et konkavt hjørne.

Da O og Q ligger inden for polygonen (eller på dens grænse), ville P også skulle ligge inden for grænsen, fordi polygonen er konveks, og det hjørne, som O og Q danner med P, er konkavt i forhold til polygonen.

Dermed har vi fundet en modsigelse, hvilket betyder, at et sådant punkt P ikke kan eksistere.

Implementering

Den her leverede implementering har en funktion convex_hull, som tager en std::vector, der indeholder punkterne som std::pairs af ints, og returnerer en anden std::vector, der indeholder de punkter, der ligger på det konvekse skrog.

Runtime og hukommelsesanalyse

Det er altid nyttigt at tænke på kompleksitetsalgoritmerne i form af Big-O-notationen, som jeg ikke vil forklare her, fordi Michael Olorunnisola her allerede har forklaret det meget bedre, end jeg sandsynligvis ville gøre:

Sortering af punkterne tager i første omgang O(n log n) tid, men derefter kan hvert trin beregnes på konstant tid. Hvert punkt bliver tilføjet til og fjernet fra stakken højst én gang, hvilket betyder, at den værst tænkelige løbetid ligger på O(n log n).

Hukommelsesforbruget, som ligger på O(n) i øjeblikket, kunne optimeres ved at fjerne behovet for stakken og udføre operationerne direkte på inputarrayen. Vi kunne flytte de punkter, der ligger på det konvekse skrog, til begyndelsen af input arrayet og arrangere dem i den rigtige rækkefølge, og de andre punkter ville blive flyttet til resten af arrayet. Funktionen kunne så blot returnere en enkelt heltalsvariabel, der angiver antallet af punkter i arrayet, der ligger på det konvekse skrog. Dette har selvfølgelig den ulempe, at funktionen bliver meget mere kompliceret, jeg vil derfor fraråde det, med mindre du koder til indlejrede systemer eller har lignende restriktive hukommelseshensyn. I de fleste situationer er afvejningen fejlsandsynlighed/hukommelsesbesparelse bare ikke det værd.

Andre algoritmer

Et alternativ til Graham Scan er Chans algoritme, som er baseret på effektivt den samme idé, men som er nemmere at implementere. Det giver dog god mening først at forstå, hvordan Graham Scan fungerer.

Hvis du virkelig føler dig smart og ønsker at løse problemet i tre dimensioner, så tag et kig på Preparata og Hongs algoritme, der blev introduceret i deres artikel fra 1977 “Convex Hulls of Finite Sets of Points in Two and Three Dimensions”.