En kort introduktion til differentiel fortrolighed
Aaruran Elamurugaiyan
Privatliv kan kvantificeres. Endnu bedre er det, at vi kan rangordne strategier til bevarelse af privatlivets fred og sige, hvilken der er mest effektiv. Endnu bedre er det, at vi kan udforme strategier, der er robuste, selv over for hackere, der har supplerende oplysninger. Og som om det ikke var godt nok, kan vi gøre alle disse ting på samme tid. Disse og flere andre løsninger findes i en probabilistisk teori, der kaldes differentielt privatliv.
Her er sammenhængen. Vi kuraterer (eller administrerer) en følsom database og vil gerne frigive nogle statistikker fra disse data til offentligheden. Vi skal imidlertid sikre, at det er umuligt for en modstander at reverse-engineere de følsomme data ud fra det, vi har frigivet . En modstander er i dette tilfælde en part, der har til hensigt at afsløre eller få kendskab til i det mindste nogle af vores følsomme data. Differentielt privatliv kan løse problemer, der opstår, når disse tre ingredienser – følsomme data, kuratorer, der skal frigive statistikker, og modstandere, der ønsker at genfinde de følsomme data – er til stede (se figur 1). Denne reverse-engineering er en form for brud på privatlivets fred.

Men hvor svært er det at bryde privatlivets fred? Ville det ikke være godt nok at anonymisere dataene? Hvis man har hjælpeoplysninger fra andre datakilder, er anonymisering ikke nok. I 2007 frigav Netflix f.eks. et datasæt af deres brugerbedømmelser som led i en konkurrence for at se, om nogen kunne overgå deres kollaborative filtreringsalgoritme. Datasættet indeholdt ikke personligt identificerbare oplysninger, men forskerne var stadig i stand til at bryde privatlivets fred; de genvandt 99 % af alle de personlige oplysninger, der blev fjernet fra datasættet . I dette tilfælde krænkede forskerne privatlivets fred ved hjælp af hjælpeoplysninger fra IMDB.
Hvordan kan man forsvare sig mod en modstander, der har ukendt og muligvis ubegrænset hjælp fra omverdenen? Differentielt privatliv tilbyder en løsning. Differentielt private algoritmer er modstandsdygtige over for adaptive angreb, der anvender hjælpeoplysninger . Disse algoritmer er afhængige af at inkorporere tilfældig støj i blandingen, så alt, hvad en modstander modtager, bliver støjende og upræcist, og så det er meget vanskeligere at bryde privatlivets fred (hvis det overhovedet er muligt).
Noisy Counting
Lad os se på et simpelt eksempel på indsprøjtning af støj. Lad os antage, at vi forvalter en database med kreditvurderinger (opsummeret i tabel 1).
Lad os i dette eksempel antage, at modstanderen ønsker at kende antallet af personer, der har en dårlig kreditvurdering (hvilket er 3). Dataene er følsomme, så vi kan ikke afsløre den grundlæggende sandhed. I stedet vil vi bruge en algoritme, der returnerer grundsandheden, N = 3, plus noget tilfældig støj. Denne grundlæggende idé (at tilføje tilfældig støj til grundsandheden) er nøglen til differentielt privatliv. Lad os sige, at vi vælger et tilfældigt tal L fra en nul-centreret Laplace-fordeling med en standardafvigelse på 2. Vi returnerer N+L. Vi vil forklare valget af standardafvigelse i et par afsnit. (Hvis du ikke har hørt om Laplace-fordelingen, kan du se figur 2). Vi vil kalde denne algoritme for “noisy counting”.
Hvis vi skal rapportere et meningsløst, støjende svar, hvad er så meningen med denne algoritme? Svaret er, at den giver os mulighed for at finde en balance mellem nytteværdi og privatlivets fred. Vi ønsker, at offentligheden skal få en vis nytteværdi af vores database uden at udsætte følsomme data for en eventuel modstander.
Hvad ville modstanderen egentlig få? Svarene er rapporteret i tabel 2.

Det første svar, som modstanderen modtager, ligger tæt på, men er ikke lig med grundsandheden. I den forstand bliver modstanderen narret, nytteværdien er sikret, og privatlivets fred er beskyttet. Men efter flere forsøg vil de være i stand til at estimere den grundlæggende sandhed. Denne “vurdering på grundlag af gentagne forespørgsler” er en af de grundlæggende begrænsninger for differentielt privatliv . Hvis modstanderen kan foretage tilstrækkeligt mange forespørgsler til en differentielt privat database, kan han stadig vurdere de følsomme data. Med andre ord, med flere og flere forespørgsler krænkes privatlivets fred. Tabel 2 viser empirisk denne krænkelse af privatlivets fred. Som man kan se, er det 90 % konfidensinterval fra disse 5 forespørgsler imidlertid ret bredt; skønnet er endnu ikke særlig præcist.
Hvor præcist kan dette skøn være? Tag et kig på figur 3, hvor vi har kørt en simulering flere gange og plottet resultaterne .

Hver lodret linje illustrerer bredden af et 95 % konfidensinterval, og punkterne angiver gennemsnittet af modstanderens udtagne data. Bemærk, at disse diagrammer har en logaritmisk vandret akse, og at støjen er udtrukket fra uafhængige og identisk distribuerede Laplace-tilfældsvariabler. Generelt er middelværdien mere støjende med færre forespørgsler (da stikprøvestørrelserne er små). Som forventet bliver konfidensintervallerne smallere, efterhånden som modstanderen foretager flere forespørgsler (da stikprøvestørrelsen øges, og støjen bliver i gennemsnit lig nul). Bare ved at inspicere grafen kan vi se, at det kræver ca. 50 forespørgsler at lave et anstændigt skøn.
Lad os reflektere over dette eksempel. Først og fremmest har vi ved at tilføje tilfældig støj gjort det sværere for en modstander at krænke privatlivets fred. For det andet var den skjulestrategi, vi anvendte, enkel at gennemføre og forstå. Desværre var modstanderen med flere og flere forespørgsler i stand til at tilnærme sig det sande antal.
Hvis vi øger variansen af den tilføjede støj, kan vi bedre forsvare vores data, men vi kan ikke blot tilføje en hvilken som helst Laplace-støj til en funktion, som vi ønsker at skjule. Årsagen er, at den mængde støj, vi skal tilføje, afhænger af funktionens følsomhed, og hver funktion har sin egen følsomhed. Især har tællefunktionen en følsomhed på 1. Lad os se på, hvad følsomhed betyder i denne sammenhæng.
Følsomhed og Laplace-mekanismen
For en funktion:
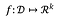
Følsomheden for f er:
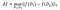
på datasæt D₁, D₂, der adskiller sig på højst ét element .
Overstående definition er ret matematisk, men den er ikke så slem, som den ser ud. Groft sagt er følsomheden af en funktion den størst mulige forskel, som en række kan have på resultatet af den pågældende funktion, for ethvert datasæt. For eksempel har optælling af antallet af rækker i vores legetøjsdatasæt en følsomhed på 1, fordi tilføjelse eller fjernelse af en enkelt række fra ethvert datasæt højst vil ændre tallet med 1.
Som et andet eksempel kan vi antage, at vi tænker på “tæller afrundet op til et multiplum af 5”. Denne funktion har en følsomhed på 5, og det kan vi ret nemt vise. Hvis vi har to datasæt af størrelsen 10 og 11, er de forskellige på én række, men “antal afrundet op til et multiplum af 5” er henholdsvis 10 og 15. Faktisk er fem den størst mulige forskel, som denne eksempelfunktion kan give. Derfor er dens følsomhed 5.
Det er vanskeligt at beregne følsomheden for en arbitrær funktion. En betydelig forskningsindsats er brugt på at estimere følsomheder , forbedre estimater af følsomhed og omgå beregningen af følsomhed .
Hvordan hænger følsomhed sammen med støjende tælling? Vores strategi for støjende tælling anvendte en algoritme kaldet Laplace-mekanismen, som igen er afhængig af følsomheden af den funktion, den skjuler . I Algoritme 1 har vi en naiv pseudokodeimplementering af Laplace-mekanismen .
Algoritme 1
Input: Funktion F, input X, fortrolighedsniveau ϵ
Output: A Noisy Answer
Beregne F (X)
Beregne følsomhed af af F : S
Træk støj L fra en Laplace-fordeling med varians:
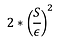
Returner F(X) + L
Desto større følsomhed S, desto mere støjende bliver svaret. Optælling har kun en følsomhed på 1, så vi behøver ikke at tilføje en masse støj for at bevare privatlivets fred.
Bemærk, at Laplace-mekanismen i Algoritme 1 bruger en parameter epsilon. Vi vil henvise til denne størrelse som mekanismens tab af privatlivets fred og er en del af den mest centrale definition inden for differentielt privatliv: epsilon-differentielt privatliv: epsilon-differentielt privatliv. For at illustrere dette kan vi, hvis vi minder om vores tidligere eksempel og bruger noget algebra, se, at vores støjende tællemekanisme har epsilon-differentielt privatliv med en epsilon på 0,707. Ved at indstille epsilon kontrollerer vi, hvor støjende vores støjende tælling er. Hvis vi vælger en mindre epsilon, får vi mere støjsvage resultater og bedre garantier for privatlivets fred. Som reference bruger Apple en epsilon på 2 i deres tastaturers differentielt private auto-korrektion .
Mængden epsilon er, hvordan differentielt privatliv kan give stringente sammenligninger mellem forskellige strategier. Den formelle definition af epsilon-differentielt privatliv er lidt mere matematisk involveret, så jeg har med vilje udeladt den fra dette blogindlæg. Du kan læse mere om det i Dwork’s survey of differential privacy .
Som du husker det, havde det støjende tælleeksempel en epsilon på 0,707, hvilket er ret lille. Men vi overtrådte stadig privatlivets fred efter 50 forespørgsler. Hvorfor? Fordi med flere forespørgsler vokser privatlivsbudgettet, og derfor er privatlivsgarantien dårligere.
Privatlivsbudgettet
Generelt set akkumuleres tabene af privatlivets fred. Når der returneres to svar til en modstander, er det samlede tab af privatlivets fred dobbelt så stort, og privatlivsgarantien er halvt så stærk. Denne kumulative egenskab er en konsekvens af kompositionsteoremet. Med hver ny forespørgsel frigives yderligere oplysninger om de følsomme data. Sætningen om sammensætning har derfor et pessimistisk synspunkt og antager det værst tænkelige scenarie: der sker den samme mængde lækage ved hvert nyt svar. For at opnå stærke garantier for privatlivets fred ønsker vi, at tabet af privatlivets fred skal være lille. Så i vores eksempel, hvor vi har et tab af privatlivets fred på femogtredive(efter 50 forespørgsler til vores Laplace-mekanisme med støjende tælling), er den tilsvarende garanti for privatlivets fred skrøbelig.
Hvordan fungerer differentielt privatliv, hvis tabet af privatlivets fred vokser så hurtigt? For at sikre en meningsfuld garanti for privatlivets fred kan datakonservatorer håndhæve et maksimalt tab af privatlivets fred. Hvis antallet af forespørgsler overstiger tærsklen, bliver privatlivsgarantien for svag, og kuratoren holder op med at besvare forespørgsler. Det maksimale tab af privatlivets fred kaldes privatlivsbudgettet . Vi kan betragte hver forespørgsel som en “udgift” til beskyttelse af privatlivets fred, som medfører et gradvist tab af privatlivets fred. Strategien med budgetter, udgifter og tab er passende nok kendt som privacy accounting .
Privacy accounting er en effektiv strategi til at beregne tabet af privatlivets fred efter flere forespørgsler, men den kan stadig inkorporere sammensætningsteoremet. Som tidligere nævnt antager sammensætningsteoremet det værst tænkelige scenarie. Med andre ord findes der bedre alternativer.
Dyb indlæring
Dyb indlæring er et underområde inden for maskinindlæring, der vedrører træning af dybe neurale netværk (DNN’er) til at vurdere ukendte funktioner . (På et højt niveau er et DNN en sekvens af affine og ikke-lineære transformationer, der kortlægger et n-dimensionelt rum til et m-dimensionelt rum). Dens anvendelser er meget udbredte og behøver ikke at blive gentaget her. Vi vil undersøge, hvordan man privat træner et dybt neuralt netværk.
Dybe neurale netværk trænes typisk ved hjælp af en variant af stokastisk gradientafstigning (SGD). Abadi et al. opfandt en privatlivsbevarende version af denne populære algoritme, der almindeligvis kaldes “privat SGD” (eller PSGD). Figur 4 illustrerer styrken i deres nye teknik . Abadi et al. opfandt en ny fremgangsmåde: øjeblikke-regnskabsføreren. Den grundlæggende idé bag moments accountant er at akkumulere privatlivsudgifterne ved at indramme privatlivsforringelsen som en tilfældig variabel og bruge dens momentgenererende funktioner til bedre at forstå denne variabels fordeling (deraf navnet) . De fulde tekniske detaljer ligger uden for rammerne af et indledende blogindlæg, men vi opfordrer dig til at læse det originale papir for at få mere at vide.

Sluttanker
Vi har gennemgået teorien om differentielt privatliv og set, hvordan den kan bruges til at kvantificere privatlivets fred. Eksemplerne i dette indlæg viser, hvordan de grundlæggende idéer kan anvendes og sammenhængen mellem anvendelse og teori. Det er vigtigt at huske, at privatlivsgarantier forringes ved gentagen brug, så det er værd at tænke over, hvordan man kan afbøde dette, hvad enten det er med privacy budgeting eller andre strategier. Du kan undersøge forringelsen ved at klikke på denne sætning og gentage vores eksperimenter. Der er stadig mange spørgsmål, der ikke er besvaret her, og der er et væld af litteratur at udforske – se referencerne nedenfor. Vi opfordrer dig til at læse videre.
Cynthia Dwork. Differential privacy: A survey of results. International Conference on Theory and Applications of Models of Computation, 2008.
Wikipedia Bidragsydere: Wikipedia Contributors. Laplace-fordeling, juli 2018.
Aaruran Elamurugaiyan. Plots, der viser standardfejl af differentielt private svar over antallet af forespørgsler. august 2018.
Benjamin I. P. Rubinstein og Francesco Alda. Smertefri tilfældig differentiel privatlivsbeskyttelse med følsomhedsprøveudtagning. In 34th International Conference on Machine Learning (ICML’2017) , 2017.
Cynthia Dwork og Aaron Roth. Det algoritmiske grundlag for differentielt privatliv . Now Publ., 2014.
Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan Mcmahan, Ilya Mironov, Kunal Talwar og Li Zhang. Dyb indlæring med differentielt privatliv. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security – CCS16 , 2016.
Frank D. McSherry. Privacy integrerede forespørgsler: En udvidelig platform til privatlivsbevarende dataanalyse. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data , SIGMOD ’09, side 19-30, New York, NY, USA, 2009. ACM.
Wikipedia Bidragsydere. Deep Learning, august 2018.
Leave a Reply