Del 14 : Punkt- og Hadamardprodukt
Ud over den tidligere omtalte matrixmultiplikation kan vektorer multipliceres ved hjælp af yderligere to metoder : Punktprodukt og Hadamardprodukt. De resultater, der opnås ved de to metoder, er forskellige.
Eelementerne svarende til samme række og kolonne multipliceres sammen, og produkterne lægges sammen, således at resultatet er en skalar.
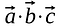
I modsætning til matrixmultiplikation er resultatet af punktproduktet ikke en anden vektor eller matrix, det er en skalar.
Rækkefølgen af vektorer er ligegyldig for punktproduktet, blot skal antallet af elementer i de to vektorer være lige stort.
Den geometriske formel for prikproduktet er
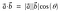
Punktproduktet kaldes også indre produkt eller skalarprodukt.
Projektion af vektor
Antag, at vi har to vektorer c og d, der er underlagt vinklen, phi(Ф).
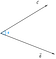
Nu, kan projektionen af vektor c på vektor d repræsenteres som
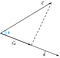
Vi kan ud fra figuren konkludere, at projektionen er lig med den horisontale komponent af vektor c med hensyn til vinklen phi(Ф).
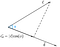
Dette kaldes skalarprojektion.For at finde vektorprojektionen af vektor c på vektor d skal vi gange skalarprojektionen med enhedsvektor d.
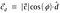
Substituering af værdien af enhedsvektor d.
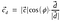
Sådan, kan punktproduktet også repræsenteres som
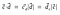
Projektioner har bred anvendelse i lineær algebra og maskinlæring (Support Vector Machine(SVM) er en maskinlæringsalgoritme, der anvendes til klassificering af data).
Hadamardprodukt (elementvis multiplikation)
Hadamardproduktet af to vektorer ligner meget matrixaddition, hvor elementer svarende til samme række og kolonner i givne vektorer/matricer multipliceres sammen for at danne en ny vektor/matrix.
Det er opkaldt efter den franske matematiker Jacques Hadamard.
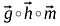
Rækkefølgen af de matricer/vektorer, der skal multipliceres, skal være den samme, og den resulterende matrix vil også være af samme rækkefølge.
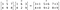

Hadamardproduktet anvendes i billedkomprimeringsteknikker som f.eks. JPEG. Det er også kendt som Schur-produktet efter den tyske matematiker Issai Schur.
Hadamard-produktet anvendes i LSTM-celler (Long Short-Term Memory) i recurrent Neural Networks (RNNs).
Leave a Reply