Bilinear filtrering og bilinear interpolation

Kig på billedet nedenfor. Kan du beregne værdierne i punkterne A,B og C?

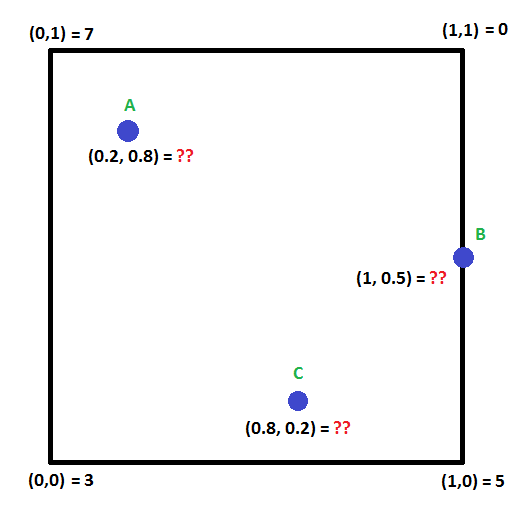
Der findes en teknik til at gøre dette, der kaldes bilinear interpolation, som udvider ideen om lineær interpolation til to dimensioner.

For at beregne bilinear interpolation foretager du blot lineær interpolation på den ene akse og derefter på den anden.

Kig på disse eksempler:

Punkt A
Punkt A har en koordinat på (0,2,0,8). Lad os starte med X-aksen.

Først foretager vi interpolation hen over toppen af kvadratet på X-aksen. Det betyder, at vi skal gå 0,2 (20 %) af vejen fra 7 til 0. Denne 0,2 er vores x-aksekoordinat. For at beregne det gør vi dette:
7 + (0-7) * 0,2 = 5,6

Næst foretager vi interpolation hen over bunden af kvadratet på X-aksen. Så i lighed med ovenfor går vi 0,2 (20%) af vejen fra 3 til 5. For at beregne det gør vi således:
3 + (5-3) * 0,2 = 3,4

Nu da vi har interpoleret på tværs af vores X-akse, skal vi interpolere på tværs af vores Y-akse. Vi skal nu gå 0,8 (80 %) af vejen fra vores nederste værdi (værdien af Y = 0) til vores øverste værdi (værdien af Y = 1). Den nederste værdi er den nederste interpolation, vi foretog (3,4), og den øverste værdi er den øverste interpolation, vi foretog (5,6).

Sådan skal vi gå 0,8 (80 %) af vejen fra 3,4 til 5,6. For at beregne det gør vi dette:
3,4 + (5,6 – 3,4) * 0,8 = 5,16

Så værdien i punkt A er 5,16. Billedet nedenfor skulle hjælpe med at forklare visuelt den proces, vi gik igennem.

Punkt B

Punkt B har koordinaterne (1,0,0,5).

Lad os starte med X-aksens interpolation igen (selvom du sagtens kunne starte med Y først, hvis du ville! Du ville ende med det samme resultat).

Gør vi X-akseinterpolationen på tværs af toppen, skal vi gå 1,0 (100 %) af vejen fra 7 til 0. Du kan sikkert gætte svaret, men her er det udregnet:
7 + (0-7) * 1,0 = 0

Lad os på samme måde lave X-akseinterpolationen på tværs af bunden. Vi skal gå 1,0 (100 %) af vejen fra 3 til 5.
3 + (5-3) * 1,0 = 5

Næste punkt er interpolationen af Y-aksen. Vi skal gå 0,5 (50 %) af vejen fra 5 til 0.
5 + (0-5) * 0,5 = 2,5

Der er vi, værdien i punkt B er 2,5. Det burde også give mening ved at se på diagrammet. Det er dybest set 1d lineær interpolation mellem 5 og 0, og ligger halvvejs imellem dem, så intuitivt burde svaret 2,5 give mening.

Punkt C

Punkt C har en koordinat på (0,8,0,2).

Endnu engang, lad os lave X-aksens interpolation hen over toppen af kassen. Vi skal gå 0,8 (80 %) af vejen fra 7 til 0.
7 + (0-7) * 0,8 = 1,4

Dernæst skal vi foretage x-akseinterpolationen på tværs af bunden af boksen. Vi skal gå 0,8 (80 %) af vejen fra 3 til 5.
3 + (5-3) * 0,8 = 4,6

Sidst skal vi foretage interpolationen af y-aksen. Vi skal gå 0,2 (20 %) fra 4,6 til 1,4.
4,6 + (1,4-4,6) * 0,2 = 3,96

Værdien af punkt C er 3.96

Bilineær filtrering

Mens bilineær interpolation er nyttig, hvis du har et gitter af data, som du ønsker at interpolere værdier inden for (f.eks. et højdefelt, der repræsenterer terræn?!), er der, hvor dette virkelig skinner i spiludvikling, i bilineær teksturfiltrering.

Grundlæggende, når du har en teksturkoordinat, der ikke er perfekt på linje med midten af en pixel i tekstur (fordi der er en rest), bruger den den brøkdel af koordinaten inden for denne pixel til at lave bilineær interpolation mellem de 4 involverede pixels for at komme frem til den endelige pixelfarve. Den foretager bilinear interpolation på hver af kanalerne: Rød, grøn, blå og alfa.

Det endelige resultat er ret godt! Tjek billedet nedenfor for at se det i aktion på en tekstur, som vi har zoomet for langt ind på. Den venstre side bruger bilinear filtrering, mens den højre side ikke gør det og bare viser dig den nærmeste pixel.

Følgelig skal bilinear teksturfiltrering lave 4 pixelaflæsninger for at kunne interpolere mellem dem, i stedet for en enkelt pixelaflæsning, som når man laver nearest pixel sampling. Flere pixelreads = mere overhead, og ikke så billigt (beregningsmæssigt) at bruge.

Links

For nogle folk, der læser dette, er denne info ret grundlæggende, og du undrer dig måske over, hvorfor jeg gider skrive om det. Kig til næste indlæg for noget lidt bizart vedrørende bilinear filtrering. Dette var nødvendigt som et springbræt til den næste ting, jeg vil vise jer 😛

Wikipedia: Linear Interpolation

Wikipedia: Linear Interpolation

Wikipedia: Bilinear Interpolation

Wikipedia: Bilinear Interpolation

Wikipedia: Bilinear Filtering

The Dark Side of Bilinear Filtering

Kig på disse links for mere dybdegående info om nogle mangler (og nogle løsninger) ved hardware-baseret bilinear sampling:
iq: hardware interpolation
iq: improved texture interpolation