9.5 – Identifikation af indflydelsesrige datapunkter

I dette afsnit lærer vi følgende to foranstaltninger til identifikation af indflydelsesrige datapunkter:

• Difference in Fits (DFFITS)
• Cook’s Distances

Den grundlæggende idé bag hver af disse foranstaltninger er den samme, nemlig at slette observationerne én ad gangen, og hver gang genindpasse regressionsmodellen på de resterende n-1 observationer. Derefter sammenligner vi resultaterne ved hjælp af alle n observationer med resultaterne, hvor den i’te observation er slettet, for at se, hvor stor indflydelse observationen har på analysen. Analyseret som sådan er vi i stand til at vurdere den potentielle indflydelse, som hvert datapunkt har på regressionsanalysen.

Difference in Fits (DFFITS)

Differencen i fits for observation i, betegnet DFFITSi, er defineret som:

\

Som det fremgår, måler tælleren forskellen i de forudsagte svar, der opnås, når det i’te datapunkt er medtaget og udelukket fra analysen. Nævneren er den anslåede standardafvigelse af forskellen i de forudsagte svar. Forskellen i tilpasninger kvantificerer derfor det antal standardafvigelser, som den tilpassede værdi ændrer sig, når det i’te datapunkt udelades.

En observation anses for at være indflydelsesrig, hvis den absolutte værdi af dens DFFITS-værdi er større end:

\

hvor som altid n = antallet af observationer og k = antallet af prædiktortermer (dvs. antallet af regressionsparametre eksklusive interceptet). Det er vigtigt at huske på, at dette ikke er en fast regel, men kun en retningslinje! Det er ikke svært at finde forskellige forfattere, der anvender en lidt anderledes retningslinje. Derfor foretrækker jeg ofte en meget mere subjektiv retningslinje, som f.eks. at et datapunkt anses for at være indflydelsesrigt, hvis den absolutte værdi af dets DFFITS-værdi stikker ud som en øm tommelfinger fra de andre DFFITS-værdier. Dette er naturligvis en kvalitativ vurdering, måske som det bør være, da outliers i sagens natur er subjektive størrelser.

Eksempel nr. 2 (igen). Lad os tjekke forskellen i tilpasningsmålet for dette datasæt (influence2.txt):

Regresserer vi y på x og anmoder om forskellen i tilpasninger, får vi følgende softwareoutput:

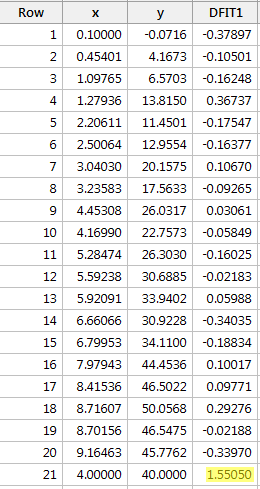
Ved anvendelse af den objektive retningslinje, der er defineret ovenfor, anser vi et datapunkt for at være indflydelsesrigt, hvis den absolutte værdi af dets DFFITS-værdi er større end:

\

Kun ét datapunkt – det røde – har en DFFITS-værdi, hvis absolutte værdi (1.55050) er større end 0,82. På baggrund af denne retningslinje vil vi derfor betragte det røde datapunkt som indflydelsesrigt.

Eksempel 3 (igen). Lad os tjekke forskellen i tilpasningsmålet for dette datasæt (influence3.txt):

Regresserer vi y på x og anmoder om forskellen i tilpasninger, får vi følgende softwareoutput:

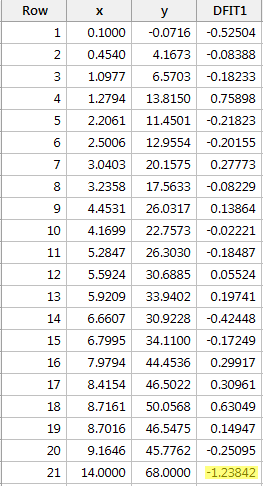
Ved anvendelse af den objektive retningslinje, der er defineret ovenfor, anser vi et datapunkt for at være indflydelsesrigt, hvis den absolutte værdi af dets DFFITS-værdi er større end:

Kun ét datapunkt – det røde – har en DFFITS-værdi, hvis absolutte værdi (1.23841) er større end 0,82. På baggrund af denne retningslinje ville vi derfor betragte det røde datapunkt som indflydelsesrigt.

Da vi studerede dette datasæt i begyndelsen af denne lektion, besluttede vi, at det røde datapunkt ikke påvirkede regressionsanalysen ret meget. Men her tyder forskellen i tilpasningsmålet på, at det faktisk er indflydelsesrigt. Hvad er det, der foregår her? Det handler om at erkende, at alle målinger i denne lektion blot er værktøjer, der markerer potentielt indflydelsesrige datapunkter for dataanalytikeren. I sidste ende bør analytikeren analysere datasættet to gange – en gang med og en gang uden de markerede datapunkter. Hvis datapunkterne ændrer resultatet af regressionsanalysen væsentligt, bør forskeren rapportere resultaterne af begge analyser.

Hvis vi i dette eksempel her bruger den mere subjektive retningslinje om, hvorvidt den absolutte værdi af DFFITS-værdien stikker ud som en øm tommelfinger, vil vi sandsynligvis ikke betragte det røde datapunkt som værende indflydelsesrigt. Den næststørste DFFITS-værdi (i absolut værdi) er trods alt 0,75898. Denne DFFITS-værdi er ikke så forskellig fra DFFITS-værdien for vores “indflydelsesrige” datapunkt.

Eksempel 4 (igen). Lad os tjekke forskellen i tilpasningsmålet for dette datasæt (influence4.txt):

Regresserer vi y på x og anmoder om forskellen i tilpasninger, får vi følgende softwareoutput:

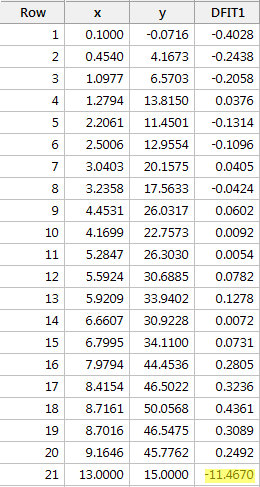
Ved anvendelse af den objektive retningslinje, der er defineret ovenfor, anser vi igen et datapunkt for at være indflydelsesrigt, hvis den absolutte værdi af dets DFFITS-værdi er større end:

\

Hvad mener du? Er der nogen af DFFITS-værdierne, der stikker ud som en øm tommelfinger? Errr – DFFITS-værdien for det røde datapunkt (-11,4670 ) er helt sikkert af en anden størrelsesorden end alle de andre. I dette tilfælde bør der ikke være megen tvivl om, at det røde datapunkt er indflydelsesrig!

Cook’s Distance

Der skal lige springes ind her, og Cooks afstandsmåling, betegnet Di, er defineret som:

\.\]

Det ser lidt rodet ud, men det vigtigste at erkende er, at Cook’s Di afhænger både af restværdien, ei (i det første udtryk), og af løftestangen, hii (i det andet udtryk). Det vil sige, at både x-værdien og y-værdien af datapunktet spiller en rolle i beregningen af Cooks afstand.

Kort sagt:

• Di opsummerer direkte, hvor meget alle de tilpassede værdier ændrer sig, når den i’te observation slettes.
• Et datapunkt med en stor Di indikerer, at datapunktet har stor indflydelse på de tilpassede værdier.

Lad os undersøge, hvad det første udsagn præcist betyder i forbindelse med nogle af vores eksempler.

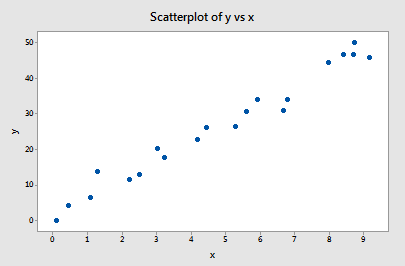
Eksempel 1 (igen). Du husker måske, at plottet af disse data (influence1.txt) tyder på, at der ikke er nogen outliers eller indflydelsesrige datapunkter for dette eksempel:

Hvis vi regresserer y på x ved hjælp af alle n = 20 datapunkter, bestemmer vi, at den estimerede interceptkoefficient b0 = 1,732 og den estimerede hældningskoefficient b1 = 5,117. Hvis vi fjerner det første datapunkt fra datasættet og regresserer y på x ved hjælp af de resterende n = 19 datapunkter, finder vi, at den estimerede interceptkoefficient b0 = 1,732 og den estimerede hældningskoefficient b1 = 5,1169. Som vi håber og forventer, ændrer estimaterne sig ikke så meget, når vi fjerner det ene datapunkt. Hvis vi fortsætter denne proces med at fjerne hvert datapunkt et ad gangen og plotte de resulterende estimerede hældninger (b1) over for de estimerede skæringspunkter (b0), får vi:

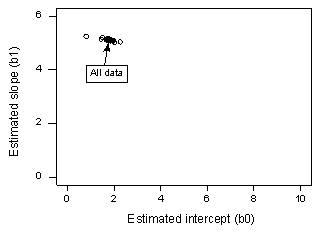
Det gennemgående sorte punkt repræsenterer de estimerede koefficienter baseret på alle n = 20 datapunkter. De åbne cirkler repræsenterer hver af de estimerede koefficienter, der er opnået ved at slette hvert datapunkt et ad gangen. Som det fremgår, er de estimerede koefficienter alle samlet, uanset hvilket datapunkt der fjernes, hvis der overhovedet fjernes et datapunkt. Dette tyder på, at intet datapunkt påvirker den estimerede regressionsfunktion og dermed de tilpassede værdier unødigt meget. I dette tilfælde ville vi forvente, at alle Cooks afstandsmål, Di, ville være små.

Eksempel 4 (igen). Du husker måske, at plottet af disse data (influence4.txt) tyder på, at et datapunkt er indflydelsesrigt og en outlier for dette eksempel:

Hvis vi regresserer y på x ved hjælp af alle n = 21 datapunkter, bestemmer vi, at den estimerede interceptkoefficient b0 = 8,51 og den estimerede hældningskoefficient b1 = 3,32. Hvis vi fjerner det røde datapunkt fra datasættet og regresserer y på x ved hjælp af de resterende n = 20 datapunkter, finder vi, at den estimerede interceptkoefficient b0 = 1,732 og den estimerede hældningskoefficient b1 = 5,1169. Wow-estimaterne ændrer sig væsentligt, når man fjerner det ene datapunkt. Hvis vi fortsætter denne proces med at fjerne hvert datapunkt et ad gangen og plotte de resulterende estimerede hældninger (b1) over for de estimerede skæringspunkter (b0), får vi:

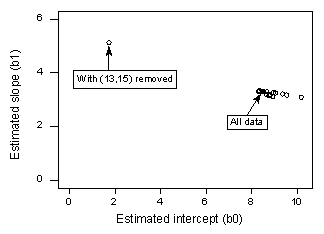
Det gennemgående sorte punkt repræsenterer igen de estimerede koefficienter baseret på alle n = 21 datapunkter. De åbne cirkler repræsenterer hver af de estimerede koefficienter, der opnås, når man sletter hvert datapunkt et ad gangen. Som du kan se, er de estimerede koefficienter med undtagelse af det røde datapunkt (x = 13, y = 15) alle samlet, uanset hvilket datapunkt der eventuelt fjernes. Dette tyder på, at det røde datapunkt er det eneste datapunkt, der påvirker den estimerede regressionsfunktion og dermed de tilpassede værdier urimeligt meget. I dette tilfælde ville vi forvente, at Cooks afstandsmål Di for det røde datapunkt er stort, og at Cooks afstandsmål Di for de resterende datapunkter er små.

Anvendelse af Cooks afstandsmål. Det smukke ved ovenstående eksempler er, at det er muligt at se, hvad der foregår med enkle plot. Desværre kan vi ikke stole på simple plots i tilfælde af multipel regression. I stedet må vi stole på retningslinjer for at afgøre, hvornår et Cook’s afstandsmål er stort nok til at retfærdiggøre, at et datapunkt behandles som indflydelsesrigt.

Her er de retningslinjer, der almindeligvis anvendes:

• Hvis Di er større end 0,5, så er det i’te datapunkt værd at undersøge nærmere, da det kan være indflydelsesrigt.
• Hvis Di er større end 1, er det i-te datapunkt ret sandsynligt, at det er indflydelsesrigt.
• Eller, hvis Di stikker ud som en øm tommelfinger fra de andre Di-værdier, er det næsten helt sikkert indflydelsesrig.

Eksempel nr. 2 (igen). Lad os tjekke Cook’s afstandsmåling for dette datasæt (influence2.txt):

Regresserer vi y på x og anmoder om Cooks afstandsmål, får vi følgende softwareoutput:

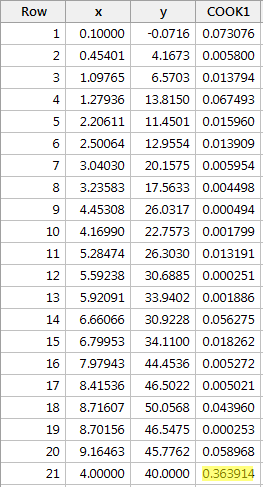
Cook’s afstandsmål for det røde datapunkt (0,363914) skiller sig en smule ud i forhold til de andre Cook’s afstandsmål. Alligevel er Cook’s afstandsmåling for det røde datapunkt mindre end 0,5. På grundlag af Cook’s afstandsmåling ville vi derfor ikke klassificere det røde datapunkt som værende indflydelsesrigt.

Eksempel 3 (igen). Lad os tjekke Cook’s afstandsmåling for dette datasæt (influence3.txt):

Regresserer vi y på x og anmoder om Cooks afstandsmål, får vi følgende softwareoutput:

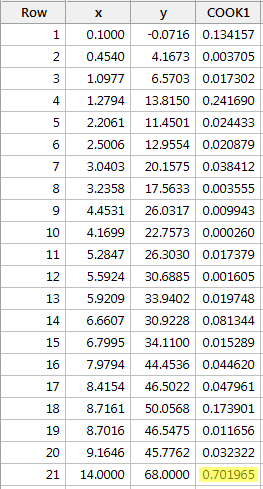
Cook’s afstandsmål for det røde datapunkt (0,701965) skiller sig en smule ud i forhold til de andre Cook’s afstandsmål. Alligevel er Cook’s afstandsmåling for det røde datapunkt større end 0,5, men mindre end 1. Derfor ville vi på grundlag af Cook’s afstandsmåling måske undersøge yderligere, men ikke nødvendigvis klassificere det røde datapunkt som værende indflydelsesrigt.

Eksempel 4 (igen). Lad os undersøge Cooks afstandsmåling for dette datasæt (influence4.txt):

Gennem at regressere y på x og anmode om Cooks afstandsmålinger får vi følgende softwareoutput:

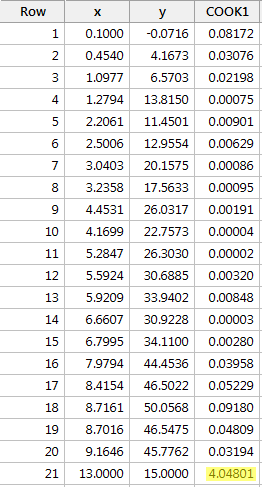
I dette tilfælde er Cooks afstandsmåling for det røde datapunkt (4.04801) skiller sig markant ud i forhold til de andre Cook’s afstandsmål. Desuden er Cook’s afstandsmåling for det røde datapunkt større end 1. Derfor vil vi på grundlag af Cook’s afstandsmåling – og ikke overraskende – klassificere det røde datapunkt som indflydelsesrigt.

En alternativ metode til fortolkning af Cook’s afstand, som nogle gange anvendes, er at relatere målingerne til F(k+1, n-k-1)-fordelingen og finde den tilsvarende percentilværdi. Hvis denne percentil er mindre end ca. 10 eller 20 procent, har sagen tilsyneladende kun ringe indflydelse på de tilpassede værdier. Hvis den derimod er tæt på 50 % eller endnu højere, har sagen en stor indflydelse. (Alt “derimellem” er mere tvetydigt.)