Zavedení konzistentního heslování

S nástupem distribuovaných architektur se konzistentní hašování stalo hlavním proudem. Co to ale přesně je a jak se liší od standardního hashovacího algoritmu? Jaké jsou jeho přesné motivace?

Nejprve si popíšeme hlavní pojmy. Poté pronikneme do existujících algoritmů, abychom pochopili problémy spojené s konzistentním hashováním.

Hashování

Hashování je proces mapování dat libovolné velikosti na hodnoty pevné velikosti. Každý existující algoritmus má svou vlastní specifikaci:

• MD5 vytváří 128bitové hodnoty hash.
• SHA-1 vytváří 160bitové hodnoty hash.
• atd.

Hashing má v informatice mnoho aplikací. Jednou z těchto aplikací je například tzv. kontrolní součet. K ověření integrity datové sady je možné použít hashovací algoritmus. Server zahesluje datovou sadu a hodnotu hashe sdělí klientovi. Klient pak zahesluje svou verzi datové sady a porovná hodnoty hash. Pokud jsou stejné, měla by být ověřena integrita.

Důležité je zde slovo „měla“. V nejhorším případě dojde ke kolizi. Kolize nastane, když dvě různé části dat mají stejnou hodnotu hash. Uveďme si reálný příklad definováním následující hašovací funkce: Při zadání osoby vrátí datum jejího narození (den & měsíc narození). Narozeninový paradox nám říká, že pokud máme v místnosti pouze 23 osob, je pravděpodobnost, že dvě osoby budou mít stejné datum narození (tedy kolize), více než 50 %. Proto funkce narozenin pravděpodobně není dobrou hašovací funkcí.

Jako rychlý úvod o hašování je důležité pochopit, že hlavní myšlenkou je rozprostření hodnot po doméně. Například:

• MD5 rozprostírá hodnoty po 128bitové prostorové doméně
• Hashovací tabulka (nebo hashmap) podpořená polem o 32 prvcích má vnitřní hashovací funkci, která rozprostírá hodnoty na libovolný index (od 0 do 31).

Rozložení zátěže

Rozložení zátěže lze definovat jako proces rozprostření zátěže po uzlech. Pojem uzel je zde zaměnitelný se serverem nebo instancí. Jedná se o výpočetní jednotku.

Rozdělování zátěže je jedním z příkladů rozdělování zátěže. Jde o rozdělení sady úloh na sadu prostředků. Například rozdělování zátěže používáme k rozdělení požadavků API mezi instance webových serverů.

Pokud jde o data, používáme spíše termín sharding. Databázový shard je horizontální oddíl dat v databázi. Typickým příkladem je databáze rozdělená na tři shardy, kde každý shard má podmnožinu celkových dat.

Vyvažování zátěže a sharding mají některé společné problémy. Například rovnoměrné rozložení dat, které zaručí, že některý uzel nebude ve srovnání s ostatními přetížen. V určitém kontextu je při vyvažování zátěže a shardingu také třeba stále přiřazovat úlohy nebo data ke stejnému uzlu:

• Potřebujeme-li serializovat, postupně zpracovávat operace pro daného spotřebitele, musíme požadavek směrovat na stejný uzel.
• Potřebujeme-li rozdělit data, musíme vědět, který shard je vlastníkem pro určitý klíč.

Zní vám to povědomě? V těchto dvou příkladech šíříme hodnoty napříč doménou. Ať už se jedná o šíření úlohy do uzlů serveru nebo o šíření dat do shardu databáze, nacházíme opět myšlenku spojenou s hashováním. To je důvod, proč lze hashování použít ve spojení s rozložením zátěže. Podívejme se, jak na to.

Mod-n hašování

Princip mod-n hašování je následující. Každý klíč je hashován pomocí hashovací funkce, která transformuje vstup na celé číslo. Poté provedeme modulo na základě počtu uzlů.

Podívejme se na konkrétní příklad se 3 uzly. Zde potřebujeme rozdělit zátěž mezi tyto uzly na základě identifikátoru klíče. Každý klíč zaheslujeme a poté provedeme operaci modulo:

Výhodou tohoto přístupu je jeho bezstavovost. Nemusíme uchovávat žádný stav, který by nám připomínal, že foo byl směrován do uzlu 2. Přesto potřebujeme vědět, kolik uzlů je nakonfigurováno pro použití operace modulo.

Jak tedy mechanismus funguje v případě škálování (přidávání nebo odebírání uzlů)? Pokud přidáme další uzel, operace modulo je nyní založena na 4 místo 3:

Jak vidíme, klíče foo a baz již nejsou přiřazeny ke stejnému uzlu. Při mod-n hašování není zaručeno zachování jakékoliv konzistence v asociaci klíč/uzel. Je to nějaký problém? Mohlo by.

Co když implementujeme datové úložiště pomocí shardingu a na základě strategie mod-n distribuujeme data? Pokud budeme škálovat počet uzlů, musíme provést operaci vyvážení. V předchozím příkladu rebalancování znamená:

• Přesunutí foo z uzlu 2 do uzlu 0.
• Přesunutí baz z uzlu 2 do uzlu 3.

Co se stane, pokud bychom měli uloženy miliony nebo dokonce miliardy dat a že bychom potřebovali rebalancovat téměř vše? Jak si dokážeme představit, jednalo by se o náročný proces. Proto musíme změnit techniku rozložení zátěže, abychom zajistili, že při rebalancování:

• Rozložení zůstane co nejrovnoměrnější na základě nového počtu uzlů.
• Počet klíčů, které musíme migrovat, by měl být omezený. V ideálním případě by to mělo být pouze 1/n procent klíčů, kde n je počet uzlů.

To je přesně účel konzistentních hashovacích algoritmů.

Termín konzistentní však může být poněkud matoucí. Setkal jsem se s inženýry, kteří předpokládali, že takové algoritmy přiřazují daný klíč stále stejnému uzlu, a to i s ohledem na škálovatelnost. Tak tomu ale není. Musí být konzistentní až do určitého bodu, aby distribuce zůstala rovnoměrná.

Nyní je čas proniknout do některých řešení.

Rendezvous

Rendezvous byl vůbec první algoritmus navržený k řešení našeho problému. Ačkoli původní studie, publikovaná v roce 1996, nezmiňuje termín konzistentní hašování, poskytuje řešení námi popsaných problémů. Podívejme se na jednu z možných implementací v jazyce Go:

Jak to funguje? Procházíme každý uzel a počítáme jeho hashovací hodnotu. Hodnotu hash vrací funkce hash, která na základě klíče (náš vstup) a identifikátoru uzlu (nejjednodušší přístup je hashovat konkatenaci těchto dvou řetězců) vytvoří celé číslo. Poté vrátíme uzel s nejvyšší hodnotou hash. To je důvod, proč je algoritmus známý také jako hashování s nejvyšší náhodnou váhou.

Hlavní nevýhodou rendezvous je jeho časová složitost O(n), kde n je počet uzlů. Je velmi efektivní, pokud potřebujeme mít omezený počet uzlů. Přesto, pokud začneme udržovat tisíce uzlů, může začít způsobovat výkonnostní problémy.

Ring Consistent Hash

Další algoritmus zveřejnili v roce 1997 Karger a kol. v tomto článku. V této studii byl poprvé zmíněn termín konzistentní hašování.

Je založen na prstenci (end-to-end propojené pole). Ačkoli se jedná o nejpopulárnější konzistentní hashovací algoritmus (nebo alespoň nejznámější), jeho princip není vždy dobře pochopen. Pojďme se do něj ponořit.

První operací je vytvoření kruhu. Prstenec má pevnou délku. V našem příkladu jej rozdělíme na 12 částí:

Poté umístíme naše uzly. V našem příkladu definujeme N0, N1 a N2.

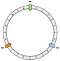
Uzly jsou prozatím rozmístěny rovnoměrně. K tomuto bodu se vrátíme později.

Pak je čas podívat se na to, jak reprezentovat klíče. Nejprve potřebujeme funkci f, která na základě klíče vrátí kruhový index (od 0 do 11). K tomu můžeme použít mod-n hašování. Protože délka kruhu je konstantní, nebude nám to činit žádný problém.

V našem příkladu budeme definovat 3 klíče: a, b a c. Na každý z nich použijeme f. Předpokládejme, že máme následující výsledky:

• f(a) = 1
• f(a) = 5
• f(a) = 7

Klíče tedy můžeme umístit na kroužek tímto způsobem:

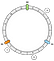
Jak přiřadíme daný klíč k uzlu? Hlavní logikou je pohyb vpřed. Z daného klíče vrátíme první uzel, který najdeme jako další při postupu vpřed:

V tomto příkladu přiřadíme a k N1, b a c k N2.

Nyní se podíváme, jak je řízeno vyvažování. Definujeme další uzel N3. Kam jej máme umístit? Již není prostor pro to, aby celkové rozdělení bylo rovnoměrné. Měli bychom uzly přeorganizovat? Ne, jinak bychom už nebyli konzistentní, že? Pro umístění uzlu znovu použijeme stejnou hashovací funkci f, kterou jsme zavedli. Místo toho, abychom ji volali pomocí klíče, můžeme ji volat pomocí identifikátoru uzlu. O pozici nového uzlu se tedy rozhoduje náhodně.

Vyvstává tedy jedna otázka: Co máme udělat s a, protože další uzel už není N1:

Řešení je následující: musíme změnit jeho asociaci a dosáhnout toho, aby a byl asociován s N3:

Jak jsme již uvedli, ideální algoritmus by měl v průměru vyvážit 1/n procent klíčů. V našem příkladu, protože přidáváme čtvrtý uzel, bychom měli mít 25 % možných klíčů reasociovaných na N3. Je tomu tak?“

• N0 z indexů 8 až 12: 33,3 % z celkového počtu klíčů
• N1 z indexů 2 až 4: 16,6 % z celkového počtu klíčů
• N2 z indexů 4 až 8: 33. V případě, že se jedná o klíče z indexů 8 až 12, je třeba provést jejich realokaci.3 % z celkového počtu klíčů
• N3 z indexů 0 až 2: 16,6 % z celkového počtu klíčů

Rozdělení není rovnoměrné. Jak to můžeme zlepšit? Řešením je použití virtuálních uzlů.

Řekněme, že místo umístění jednoho místa na uzel můžeme umístit tři. Také musíme definovat tři různé hašovací funkce. Každý uzel zaheslujeme třikrát, takže získáme tři různé indexy:

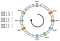
Stejný algoritmus můžeme použít při pohybu vpřed. Přesto by byl klíč přiřazen k uzlu bez ohledu na to, s jakým virtuálním uzlem se setkal.

Zrovna v tomto příkladu by nyní bylo rozložení následující:

• N0: 33,3 %
• N1: 25 %
• N2: 41,6 %

Čím více virtuálních uzlů na uzel definujeme, tím více by mělo být rozložení rovnoměrné. V průměru při 100 virtuálních uzlech na server je standardní rozložení přibližně 10 %. Při 1000 je to asi 3,2 %.

Tento mechanismus je také užitečný, pokud máme uzly s různou velikostí. Pokud je například uzel nakonfigurován tak, aby teoreticky zvládl dvakrát větší zátěž než ostatní, můžeme roztočit dvakrát více virtuálních uzlů.

Hlavní nevýhodou virtuálních uzlů je však paměťová náročnost. Pokud bychom měli obsluhovat tisíce serverů, vyžadovalo by to megabajty paměti.

Než se přesuneme dál, je zajímavé poznamenat, že někdy lze algoritmus podstatně vylepšit změnou malé části. To je například případ algoritmu zveřejněného společností Google v roce 2017 s názvem konzistentní hashování s omezeným zatížením. Tato verze je založena na stejné myšlence kruhu, kterou jsme popsali. Jejich přístup však spočívá v tom, že při každé aktualizaci (přidání/odstranění nového klíče nebo uzlu) provedou malé vyvážení. Tato verze překonává původní verzi z hlediska směrodatné odchylky s kompromisem nejhorší časové složitosti.

Skokové konzistentní hashování

V roce 2007 publikovali dva inženýři ze společnosti Google skokové konzistentní hashování. Ve srovnání s algoritmem založeným na kroužcích tato implementace „nevyžaduje žádné úložiště, je rychlejší a lépe rozděluje prostor pro klíče mezi buckety a rovnoměrně rozděluje pracovní zátěž při změně počtu bucketů“. Jinak řečeno, zlepšuje rozdělení pracovní zátěže mezi uzly (kbelík je stejný pojem jako uzel) bez jakékoli paměťové režie.

Tady je algoritmus v jazyce C++ (7 řádků kódu 🤯):

Při kruhovém konzistentním hašování byla při 1000 virtuálních uzlech směrodatná odchylka asi 3,2 %. Ve skokově konzistentním hashi již koncept virtuálních uzlů nepotřebujeme. Přesto zůstává směrodatná odchylka menší než 0,0000001 %.

Je zde však jedno omezení. Uzly musí být číslovány postupně. Pokud máme seznam serverů foo, bar a baz, nemůžeme například odstranit bar. Přesto, pokud nakonfigurujeme datové úložiště, můžeme použít algoritmus pro získání indexu oddílů na základě celkového počtu oddílů. Proto může být skokové konzistentní hashování užitečné v kontextu shardingu, ale ne v kontextu vyvažování zátěže.

Co je to algoritmus dokonalého konzistentního hashování?

Když už máme s konzistentním hašováním nějaké zkušenosti, podívejme se o krok zpět, jaký by byl dokonalý algoritmus:

• Přemístěno by bylo v průměru jen 1/n procent klíčů, kde n je počet uzlů.
• Složitost O(n) prostoru, kde n je počet uzlů.
• Časová složitost O(1) na vložení/odstranění uzlu a na vyhledání klíče.
• Minimální směrodatná odchylka, aby bylo jisté, že uzel není přetížen oproti jinému.
• Umožnil by přiřadit uzlu váhu, aby se vypořádal s různou velikostí uzlů.
• Umožnil by libovolné pojmenování uzlů (nečíslovaných postupně), aby podporoval jak vyrovnávání zátěže, tak sharding.

Naneštěstí tento algoritmus neexistuje. Na základě toho, co jsme viděli:

• Rendezvous má lineární časovou složitost na jedno vyhledávání.
• Kroužkově konzistentní hash má špatnou minimální směrodatnou odchylku bez konceptu virtuálních uzlů. S virtuálními uzly je prostorová složitost O(n*v), přičemž n je počet uzlů a v je počet virtuálních uzlů na uzel.
• Jump consistent hash nemá konstantní časovou složitost a nepodporuje libovolné jméno uzlu.

Téma je stále otevřené a existují nedávné studie, které stojí za pozornost. Například vícesondový konzistentní hash vydaný v roce 2005. Podporuje prostorovou složitost O(1). Přesto k dosažení směrodatné odchylky ε vyžaduje O(1/ε) času na jedno vyhledávání. Chceme-li například dosáhnout směrodatné odchylky menší než 0,5 %, vyžaduje to hašování klíče asi 20krát. Můžeme tedy získat minimální směrodatnou odchylku, ale za cenu vyšší časové složitosti vyhledávání.

Jak jsme uvedli v úvodu, konzistentní hashovací algoritmy se staly hlavním proudem. Nyní se používá v nespočtu systémů, jako jsou MongoDB, Cassandra, Riak, Akka atd. ať už v souvislosti s vyrovnáváním zátěže nebo distribucí dat. Přesto, jak už to v informatice bývá, každé řešení má své kompromisy.

Když už mluvíme o kompromisech, pokud potřebujete navázat, můžete se podívat na vynikající příspěvek, který napsal Damian Gryski:

.