Mathematics for the Liberal Arts
Výstupy z učení
- Definice a identifikace soběpodobnosti v geometrických tvarech, rostlinách, a geologických útvarů
- Vygenerovat fraktální tvar daný iniciátorem a generátorem
- Škálovat geometrický objekt určitým škálovacím faktorem pomocí vztahu pro škálovací rozměr
- Určit fraktální rozměr fraktálního objektu
Kromě vizuální soběpodobnosti vykazují fraktály i další zajímavé vlastnosti. Všimněte si například, že každý krok iterace Sierpińského těsnění odstraní jednu čtvrtinu zbývající plochy. Kdybychom v tomto procesu pokračovali donekonečna, skončili bychom v podstatě s odstraněním celé plochy, což znamená, že jsme začali s dvourozměrnou plochou a nějakým způsobem skončili s něčím menším, ale zdánlivě větším než jen s jednorozměrnou čarou.
Abychom mohli tuto myšlenku prozkoumat, musíme probrat rozměr. Něco jako přímka je jednorozměrné; má pouze délku. Jakákoli křivka je jednorozměrná. Věci jako krabice a kružnice jsou dvojrozměrné, protože mají délku a šířku a popisují plochu. Předměty jako krabice a válce mají délku, šířku a výšku, popisují tedy objem a jsou trojrozměrné.
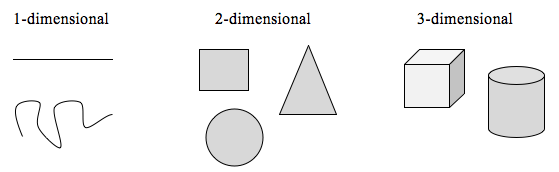
Pro škálování objektů platí určitá pravidla související s jejich rozměry.
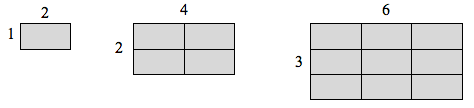
Pokud bych měl přímku o délce 1 a chtěl její délku škálovat o 2, potřeboval bych dvě kopie původní přímky. Kdybych měl čáru o délce 1 a chtěl její délku škálovat o 3, potřeboval bych tři kopie původní čáry.
Pokud bych měl obdélník o délce 2 a výšce 1 a chtěl bych jeho délku a šířku škálovat o 2, potřeboval bych čtyři kopie původního obdélníku. Kdybych chtěl jeho délku a šířku zvětšit o 3, potřeboval bych devět kopií původního obdélníku.
Pokud bych měl krychlový box se stranami o délce 1 a chtěl bych jeho délku a šířku zvětšit o 2, potřeboval bych osm kopií původní krychle. Kdybych chtěl její délku a šířku zvětšit o 3, potřeboval bych 27 kopií původní krychle.
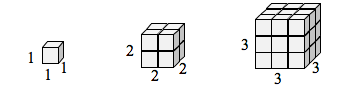
Všimněte si, že v jednorozměrném případě jsou potřebné kopie = měřítko.
V dvourozměrném případě jsou potřebné kopie = měřítko^{2}.
V třírozměrném případě jsou potřebné kopie = měřítko^{3}.
Z těchto příkladů můžeme odvodit vzorec.
Vztah mezi měřítkem a rozměrem
Chceme-li měnit měřítko D-rozměrného tvaru o měřítkový faktor S, bude počet potřebných kopií C původního tvaru dán vztahem:
\text{Kopie}=\text{Škála}^{\text{Rozměr}}, neboli C=S^{D}
Příklad
Pro určení rozměru Sierpinského těsnění použijte vztah měřítko-rozměr.
Předpokládejme, že jsme definovali původní těsnění o délce strany 1. Zobrazené větší těsnění je dvakrát širší a dvakrát vyšší, bylo tedy zmenšeno koeficientem 2.
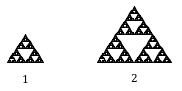
Všimněte si, že k sestrojení většího těsnění jsou potřeba 3 kopie původního těsnění.
Pomocí vztahu měřítko-rozměr C=S^{D} dostaneme rovnici 3=2^{D}.
Protože 2^{1}=2 a 2^{2}=4, okamžitě vidíme, že D je někde mezi 1 a 2; těsnění je více než jednorozměrný útvar, ale odebrali jsme mu tolik plochy, že je nyní méně než dvourozměrný.
Řešení rovnice 3=2^{D} vyžaduje logaritmy. Pokud jste se o logaritmech učili dříve, možná si vzpomenete, jak tuto rovnici řešit (pokud ne, stačí přeskočit na rámeček níže a použít tento vzorec s klávesou log na kalkulačce):
Vezměte logaritmus obou stran.
3={{2}^{D}}
Použijte exponentovou vlastnost logaritmů.
\log(3)=\log\left({{2}^{D}}\right)
Dělte log(2).
\log(3)=D\log\levá(2\pravá)
Rozměr těsnění je přibližně 1,585.
D=\frac{\log\levá(3\pravá)}{\log(2)}\aprox1.585
Závislost škálování a rozměru, zjištění rozměru
Chcete-li zjistit rozměr D fraktálu, určete faktor škálování S a počet potřebných kopií C původního tvaru, pak použijte vzorec
D=\frac{\log\left(C\right)}{\log(S)}
Zkuste to
Zjistěte fraktální rozměr fraktálu vytvořeného pomocí iniciátoru a generátoru.
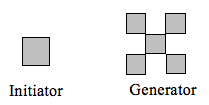
Na následujícím videu uvádíme praktický příklad, jak určit rozměr Sierpinského těsnění
.

Leave a Reply