Mírný úvod do problému konvexního trupu

Konvexní trupy bývají užitečné v mnoha různých oblastech, někdy zcela nečekaně. V tomto článku vysvětlím základní myšlenku 2d konvexních trupů a jak k jejich nalezení použít Grahamův sken. Pokud tedy již grahamův sken znáte, pak tento článek není určen pro vás, ale pokud ne, měl by vás seznámit s některými důležitými pojmy.

Konvexní plášť množiny bodů je definován jako nejmenší konvexní mnohoúhelník, který obklopuje všechny body množiny. Konvexní znamená, že mnohoúhelník nemá žádný roh ohnutý dovnitř.

Červené hrany na pravé straně mnohoúhelníku uzavírají roh, kde je útvar konkávní, tedy opak konvexního.

Užitečným způsobem, jak uvažovat o konvexním trupu, je analogie s gumičkou. Předpokládejme, že body množiny jsou hřebíky, které trčí z rovné plochy. Představte si nyní, co by se stalo, kdybyste vzali gumičku a natáhli ji kolem hřebíků. Při pokusu o smrštění zpět na původní délku by gumička hřebíky obepnula a dotkla by se těch, které trčí nejdále od středu.

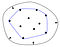
Chceme-li výsledný konvexní trup reprezentovat v kódu, obvykle ukládáme seznam bodů, které tuto gumičku drží, tj. seznam bodů na konvexním trupu.

Všimněte si, že ještě musíme definovat, co se má stát, pokud tři body leží na stejné přímce. Pokud si představíme, že gumička má bod, kde se dotýká jednoho z hřebíků, ale vůbec se tam neohýbá, znamená to, že hřebík tam leží na přímce mezi dvěma jinými hřebíky. V závislosti na úloze můžeme tento hřebík podél přímky považovat za součást výstupu, protože se dotýká gumičky. Na druhou stranu bychom také mohli říci, že tento hřebík by neměl být součástí výstupu, protože tvar gumičky se při jeho odstranění nezmění. Toto rozhodnutí závisí na problému, na kterém právě pracujete, a nejlépe, pokud máte vstup, kde žádné tři body nejsou kolineární (to je častý případ v jednoduchých úlohách pro soutěže v programování), pak můžete tento problém dokonce zcela ignorovat.

Nalezení konvexního trupu

Při pohledu na množinu bodů nám lidská intuice umožňuje rychle zjistit, které body se pravděpodobně budou dotýkat konvexního trupu a které budou blíže středu, a tedy mimo konvexní trup. Převést tuto intuici do kódu však dá trochu práce.

K nalezení konvexního trupu množiny bodů můžeme použít algoritmus zvaný Grahamův sken, který je považován za jeden z prvních algoritmů výpočetní geometrie. Pomocí tohoto algoritmu můžeme najít podmnožinu bodů, které leží na konvexním trupu, spolu s pořadím, ve kterém se tyto body při obcházení konvexního trupu vyskytují.

Algoritmus začíná nalezením bodu, o kterém s jistotou víme, že leží na konvexním trupu. Za bezpečnou volbu lze považovat například bod s nejnižší souřadnicí y. Pokud existuje více bodů se stejnou souřadnicí y, vezmeme ten, který má největší souřadnici x (to funguje i u jiných rohových bodů, např. nejprve nejnižší x a pak nejnižší y).

Dále seřadíme ostatní body podle úhlu, pod kterým leží z pohledu od výchozího bodu. Pokud se stane, že dva body leží pod stejným úhlem, měl by se bod, který je blíže výchozímu bodu, vyskytnout v třídění dříve.

Nyní je smyslem algoritmu projít toto setříděné pole a pro každý bod určit, zda leží na konvexním trupu. To znamená, že pro každou trojici bodů, na kterou narazíme, rozhodneme, zda tvoří konvexní nebo konkávní roh. Pokud je roh konkávní, pak víme, že prostřední bod z této trojice nemůže ležet na konvexním trupu.

(Všimněte si, že pojmy konkávní a konvexní roh musíme používat ve vztahu k celému mnohoúhelníku, jen roh sám o sobě nemůže být konvexní nebo konkávní, protože by neměl žádný referenční směr.)

Body, které leží na konvexním plášti, uložíme na hromádku, takže je můžeme přidat, pokud na ně cestou kolem seřazených bodů narazíme, a odebrat, pokud zjistíme, že tvoří konkávní roh.

(Přísně vzato musíme přistupovat k horním dvěma bodům zásobníku, proto místo toho použijeme std::vector, ale uvažujeme o něm jako o jakémsi zásobníku, protože nás vždy zajímá jen horních pár prvků)

Pokračujeme-li kolem seřazeného pole bodů, přidáme bod na zásobník, a pokud později zjistíme, že bod nepatří do konvexního trupu, odstraníme ho.

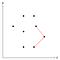
Můžeme změřit, zda se aktuální roh ohýbá dovnitř nebo ven, tak, že vypočítáme křížový součin a ověříme, zda je kladný nebo záporný. Na obrázku výše je zobrazena trojice bodů, kde roh, který tvoří, je konvexní, proto prostřední z těchto tří bodů prozatím zůstává na zásobníku.

Přejdeme-li k dalšímu bodu, postupujeme stále stejně: zkontrolujeme, zda je roh konvexní, a pokud ne, bod odstraníme. Pak pokračujeme přidáním dalšího bodu a opakujeme.

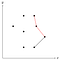
Tento roh označený červeně je konkávní, proto odstraníme prostřední bod ze zásobníku, protože nemůže být součástí konvexního trupu.

Jak víme, že nám to dá správnou odpověď?

Napsat rigorózní důkaz je nad rámec tohoto článku, ale základní myšlenky napsat mohu. Doporučuji vám však, abyste se do toho pustili a pokusili se mezery doplnit!

Protože jsme vypočítali křížový součin v každém rohu, víme jistě, že dostaneme konvexní mnohoúhelník. Teď už jen musíme dokázat, že tento konvexní mnohoúhelník opravdu uzavírá všechny body.

(Ve skutečnosti bys musel také ukázat, že je to nejmenší možný konvexní mnohoúhelník splňující tyto podmínky, ale to vyplývá celkem snadno z toho, že rohové body našeho konvexního mnohoúhelníku jsou podmnožinou původní množiny bodů.)

Předpokládejme, že existuje bod P mimo právě nalezený mnohoúhelník.

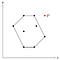
Protože každý bod byl jednou přidán na hromadu, víme, že P byl v určitém okamžiku z hromady odstraněn. To znamená, že P spolu se sousedními body, nazvěme je O a Q, tvořil konkávní roh.

Protože O a Q leží uvnitř mnohoúhelníku (nebo na jeho hranici), musel by P ležet také uvnitř hranice, protože mnohoúhelník je konvexní a roh, který O a Q tvoří s P, je vzhledem k mnohoúhelníku konkávní.

Tím jsme zjistili rozpor, což znamená, že takový bod P nemůže existovat.

Implementace

Zde uvedená implementace má funkci convex_hull, která bere std::vector, která obsahuje body jako std::pairs inty, a vrací jinou std::vector, která obsahuje body ležící na konvexním trupu.

Runtime and memory analysis

Vždy je užitečné přemýšlet o složitosti algoritmů v termínech Big-O notace, kterou zde nebudu vysvětlovat, protože Michael Olorunnisola to zde již vysvětlil mnohem lépe, než bych to pravděpodobně udělal já:

Třídění bodů zpočátku trvá O(n log n) času, ale poté lze každý krok spočítat v konstantním čase. Každý bod se na zásobník přidá a ze zásobníku odebere nanejvýš jednou, to znamená, že doba běhu v nejhorším případě leží v O(n log n).

Využití paměti, které v tuto chvíli leží v O(n), by se dalo optimalizovat odstraněním potřeby zásobníku a prováděním operací přímo na vstupním poli. Body, které leží na konvexním trupu, bychom mohli přesunout na začátek vstupního pole a uspořádat je ve správném pořadí a ostatní body by se přesunuly do zbytku pole. Funkce by pak mohla vrátit pouze jednu celočíselnou proměnnou, která by označovala množství bodů v poli, které leží na konvexním trupu. To má samozřejmě tu nevýhodu, že se funkce značně zkomplikuje, proto bych to nedoporučoval, pokud nekódujete pro vestavěné systémy nebo nemáte podobně omezující paměťové starosti. Pro většinu situací se kompromis pravděpodobnost chyby/úspora paměti prostě nevyplatí.

Jiné algoritmy

Alternativou ke Grahamovu skenování je Chanův algoritmus, který je založen na fakticky stejné myšlence, ale je jednodušší na implementaci. Má však smysl nejprve pochopit, jak Graham Scan funguje.

Pokud máte opravdu chuť a chcete řešit problém ve třech rozměrech, podívejte se na algoritmus Preparata a Honga, který představili ve svém článku „Convex Hulls of Finite Sets of Points in Two and Three Dimensions“ z roku 1977.