Krátký úvod do diferenciálního soukromí
Aaruran Elamurugaiyan
Soukromí lze vyčíslit. Ještě lépe lze seřadit strategie zachovávající soukromí a říci, která z nich je účinnější. Ještě lépe můžeme navrhnout strategie, které jsou odolné i proti hackerům, kteří mají pomocné informace. A jako by to nestačilo, můžeme všechny tyto věci dělat současně. Tato a další řešení se nacházejí v pravděpodobnostní teorii zvané diferenciální soukromí.
Tady je kontext. Spravujeme (nebo spravujeme) citlivou databázi a rádi bychom zveřejnili některé statistiky z těchto dat. Musíme však zajistit, aby bylo protivníkovi znemožněno reverzní inženýrství citlivých dat z toho, co jsme zveřejnili . Protivník je v tomto případě strana, která má v úmyslu odhalit nebo zjistit alespoň některá naše citlivá data. Diferenciální soukromí může vyřešit problémy, které vznikají, když jsou přítomny tyto tři složky – citlivá data, kurátoři, kteří potřebují zveřejnit statistiky, a protivníci, kteří chtějí citlivá data získat zpět (viz obrázek 1). Toto zpětné inženýrství je typem narušení soukromí.

Jak těžké je ale narušit soukromí? Nestačila by anonymizace údajů? Pokud máte pomocné informace z jiných zdrojů dat, anonymizace nestačí. Například v roce 2007 společnost Netflix zveřejnila datovou sadu svých uživatelských hodnocení v rámci soutěže, zda někdo dokáže překonat jejich algoritmus kolaborativního filtrování. Datová sada neobsahovala osobní identifikační údaje, ale výzkumníci přesto dokázali narušit soukromí; obnovili 99 % všech osobních údajů, které byly z datové sady odstraněny . V tomto případě výzkumníci narušili soukromí pomocí pomocných informací z IMDB.
Jak se může někdo bránit proti protivníkovi, který má neznámou a možná neomezenou pomoc z vnějšího světa? Řešení nabízí diferenciální ochrana soukromí. Diferenciálně soukromé algoritmy jsou odolné vůči adaptivním útokům, které využívají pomocné informace . Tyto algoritmy spoléhají na to, že do směsi zahrnou náhodný šum, takže vše, co protivník obdrží, se stane zašuměným a nepřesným, a tak je mnohem obtížnější prolomit soukromí (pokud je to vůbec proveditelné).
Šumové počítání
Podívejme se na jednoduchý příklad vnášení šumu. Předpokládejme, že spravujeme databázi úvěrových ratingů (shrnuje ji tabulka 1).
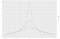
Pro tento příklad předpokládejme, že protivník chce znát počet lidí, kteří mají špatný rating (což je 3). Data jsou citlivá, takže nemůžeme odhalit základní pravdu. Místo toho použijeme algoritmus, který vrátí základní pravdu, N = 3, plus nějaký náhodný šum. Tato základní myšlenka (přidání náhodného šumu k základní pravdě) je klíčem k diferenciálnímu soukromí. Řekněme, že vybereme náhodné číslo L z nulového Laplaceova rozdělení se směrodatnou odchylkou 2. Vrátíme N+L. Volbu směrodatné odchylky vysvětlíme za několik odstavců. (Pokud jste o Laplaceově rozdělení ještě neslyšeli, podívejte se na obrázek 2). Tomuto algoritmu budeme říkat „šumové počítání“.
Pokud budeme hlásit nesmyslnou, zašuměnou odpověď, jaký smysl má tento algoritmus? Odpověď zní, že nám umožňuje dosáhnout rovnováhy mezi užitečností a soukromím. Chceme, aby široká veřejnost získala z naší databáze určitý užitek, aniž bychom případnému protivníkovi vystavili citlivé údaje.
Co by vlastně protivník získal? Odpovědi jsou uvedeny v tabulce 2.

První odpověď, kterou protivník obdrží, je blízká základní pravdě, ale není jí rovna. V tomto smyslu je protivník oklamán, užitek je zajištěn a soukromí je chráněno. Po více pokusech však bude schopen odhadnout základní pravdu. Tento „odhad z opakovaných dotazů“ je jedním ze základních omezení diferenciálního soukromí . Pokud může protivník provést dostatečný počet dotazů do diferenciálně soukromé databáze, může citlivé údaje stále odhadovat. Jinými slovy, s přibývajícími dotazy dochází k narušení soukromí. Tabulka 2 empiricky demonstruje toto narušení soukromí. Jak je však vidět, 90% interval spolehlivosti z těchto 5 dotazů je poměrně široký; odhad ještě není příliš přesný.
Jak přesný může být tento odhad? Podívejte se na obrázek 3, kde jsme několikrát spustili simulaci a vykreslili výsledky .

Každá svislá čára znázorňuje šířku 95 % intervalu spolehlivosti a body označují střední hodnotu vzorku dat protivníka. Všimněte si, že tyto grafy mají logaritmickou vodorovnou osu a že šum je vybrán z nezávislých a identicky rozdělených Laplaceových náhodných veličin. Celkově je průměr s menším počtem dotazů zašuměnější (protože velikosti vzorků jsou malé). Podle očekávání se intervaly spolehlivosti zužují s tím, jak protivník provádí více dotazů (protože velikost vzorku se zvětšuje a šum se průměruje k nule). Jen z prohlídky grafu vidíme, že ke slušnému odhadu je potřeba asi 50 dotazů.
Přemýšlejme o tomto příkladu. Především jsme přidáním náhodného šumu ztížili protivníkovi prolomení soukromí. Za druhé, námi použitá strategie skrývání byla jednoduchá na implementaci a pochopení. Bohužel s přibývajícími dotazy se protivník dokázal přiblížit skutečnému počtu.
Pokud zvýšíme rozptyl přidaného šumu, můžeme lépe bránit naše data, ale nemůžeme jednoduše přidat libovolný Laplaceův šum k funkci, kterou chceme utajit. Důvodem je, že množství šumu, které musíme přidat, závisí na citlivosti funkce, a každá funkce má svou vlastní citlivost. Konkrétně funkce počítání má citlivost 1. Podívejme se, co citlivost v tomto kontextu znamená.
Citlivost a Laplaceův mechanismus
Pro funkci:
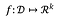
citlivost f je:
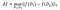
na souborech dat D₁, D₂ lišících se nejvýše v jednom prvku .
Výše uvedená definice je poměrně matematická, ale není tak špatná, jak vypadá. Zhruba řečeno, citlivost funkce je největší možný rozdíl, který může mít jeden řádek na výsledek této funkce, a to pro libovolný soubor dat. Například v naší hračkové datové sadě má počítání počtu řádků citlivost 1, protože přidání nebo odebrání jediného řádku z libovolné datové sady změní počet nejvýše o 1.
Jako další příklad si představme „počet zaokrouhlený na násobek 5“. Tato funkce má citlivost 5 a můžeme to poměrně snadno ukázat. Máme-li dva datové soubory o velikosti 10 a 11, liší se v jednom řádku, ale „počty zaokrouhlené na násobek 5“ jsou 10, respektive 15. Ve skutečnosti je pět největší možný rozdíl, který může tato příkladová funkce vytvořit. Proto je její citlivost 5.
Vypočítat citlivost pro libovolnou funkci je obtížné. Značné množství výzkumného úsilí je věnováno odhadům citlivosti , zlepšování odhadů citlivosti a obcházení výpočtu citlivosti .
Jak citlivost souvisí s počítáním šumu? Naše strategie šumového počítání používá algoritmus zvaný Laplaceův mechanismus, který zase závisí na citlivosti funkce, kterou zastírá . V algoritmu 1 máme naivní pseudokódovou implementaci Laplaceova mechanismu .
Algoritmus 1
Vstup: Funkce F, vstup X, úroveň soukromí ϵ
Výstup: Šumová odpověď
Vypočítejte F (X)
Vypočítejte citlivost F : S
Vypočítejte šum L z Laplaceova rozdělení s rozptylem:
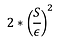
Vraťte F(X) + L
Čím větší citlivost S, tím hlučnější bude odpověď. Počítání má citlivost pouze 1, takže pro zachování soukromí nemusíme přidávat mnoho šumu
Všimněte si, že Laplaceův mechanismus v algoritmu 1 spotřebovává parametr epsilon. Tuto veličinu budeme označovat jako ztrátu soukromí mechanismu a je součástí nejstěžejnější definice v oblasti diferenciálního soukromí: epsilon-diferenciální soukromí. Pro ilustraci, vzpomeneme-li si na náš předchozí příklad a použijeme-li trochu algebry, vidíme, že náš mechanismus počítání šumu má epsilon-diferenciální soukromí, přičemž epsilon je 0,707. Nastavením epsilon kontrolujeme hlučnost našeho šumového počítání. Volbou menšího epsilonu dosáhneme hlučnějšího výsledku a lepších záruk soukromí. Jako referenci lze uvést, že společnost Apple používá ve své diferenciálně soukromé automatické opravě klávesnice hodnotu epsilon 2.
Veličina epsilon je způsob, jakým lze diferenciální soukromí přísně porovnávat mezi různými strategiemi. Formální definice diferenciálního soukromí epsilon je poněkud matematicky náročnější, proto jsem ji v tomto příspěvku záměrně vynechal. Více se o ní můžete dočíst v Dworkově přehledu diferenciálního soukromí .
Jak si vzpomínáte, příklad s počítáním šumu měl epsilon 0,707, což je poměrně málo. Ale i tak jsme po 50 dotazech narušili soukromí. Proč? Protože s rostoucím počtem dotazů roste rozpočet na soukromí, a proto se zhoršuje záruka soukromí.
Budoucnost soukromí
Všeobecně se ztráty soukromí kumulují. Když se protivníkovi vrátí dvě odpovědi, je celková ztráta soukromí dvakrát větší a záruka soukromí je o polovinu silnější. Tato kumulativní vlastnost je důsledkem věty o složení. V podstatě s každým novým dotazem se uvolní další informace o citlivých údajích. Věta o kompozici má tedy pesimistický pohled a předpokládá nejhorší možný scénář: s každou novou odpovědí dojde ke stejnému úniku informací. Pro silné záruky soukromí chceme, aby ztráta soukromí byla malá. Takže v našem příkladu, kde máme ztrátu soukromí třicet pět(po padesáti dotazech na náš Laplaceův mechanismus počítání šumu), je odpovídající záruka soukromí křehká.
Jak funguje diferenciální soukromí, když ztráta soukromí roste tak rychle? Aby byla zajištěna smysluplná záruka soukromí, mohou správci dat prosadit maximální ztrátu soukromí. Pokud počet dotazů překročí tuto hranici, záruka soukromí se stane příliš slabou a kurátor přestane na dotazy odpovídat. Maximální ztráta soukromí se nazývá rozpočet soukromí . Každý dotaz si můžeme představit jako „výdaj“ na ochranu soukromí, který způsobuje přírůstkovou ztrátu soukromí. Strategie použití rozpočtů, výdajů a ztrát se příhodně nazývá účtování soukromí .
Účtování soukromí je efektivní strategií pro výpočet ztráty soukromí po více dotazech, ale může ještě zahrnovat větu o složení. Jak bylo uvedeno dříve, kompoziční teorém předpokládá nejhorší možný scénář. Jinými slovy, existují lepší alternativy.
Hluboké učení
Hluboké učení je podoblast strojového učení, která se týká trénování hlubokých neuronových sítí (DNN) pro odhad neznámých funkcí . (Na vysoké úrovni je DNN posloupnost afinních a nelineárních transformací mapujících nějaký n-rozměrný prostor do m-rozměrného prostoru). Její aplikace jsou velmi rozšířené a není třeba je zde opakovat. Prozkoumáme, jak trénovat hlubokou neuronovou síť soukromě.
Hluboké neuronové sítě se obvykle trénují pomocí varianty stochastického sestupu po gradientu (SGD). Abadi a spol. vynalezli verzi tohoto populárního algoritmu zachovávající soukromí, běžně označovanou jako „privátní SGD“ (nebo PSGD). Obrázek 4 ilustruje sílu jejich nové techniky . Abadi a kol. vynalezli nový přístup: momentový účet. Základní myšlenkou momentového účetního je kumulovat výdaje na soukromí tím, že se ztráta soukromí zarámuje jako náhodná veličina a pomocí funkcí generujících její momenty se lépe pochopí rozdělení této veličiny (odtud název) . Úplné technické podrobnosti jsou mimo rozsah úvodního příspěvku na blogu, ale doporučujeme vám přečíst si původní článek, abyste se dozvěděli více.

Závěrečné myšlenky
Probrali jsme teorii diferenciálního soukromí a viděli jsme, jak ji lze použít ke kvantifikaci soukromí. Příklady v tomto příspěvku ukazují, jak lze základní myšlenky aplikovat, a souvislost mezi aplikací a teorií. Je důležité si uvědomit, že záruky soukromí se při opakovaném používání zhoršují, takže stojí za to přemýšlet o tom, jak to zmírnit, ať už pomocí rozpočtování soukromí nebo jiných strategií. Zhoršování můžete prozkoumat kliknutím na tuto větu a zopakováním našich experimentů. Stále existuje mnoho otázek, které zde nebyly zodpovězeny, a množství literatury, kterou je třeba prozkoumat – viz odkazy níže. Doporučujeme vám číst dál.
Cynthia Dwork. Diferenciální soukromí: A survey of results (Přehled výsledků). Mezinárodní konference o teorii a aplikacích výpočetních modelů, 2008.
Přispěvatelé Wikipedie. Laplaceovo rozdělení, červenec 2018.
Aaruran Elamurugaiyan. Grafy demonstrující standardní chybu diferenciálně soukromých odpovědí v závislosti na počtu dotazů, srpen 2018.
Benjamin I. P. Rubinstein a Francesco Alda. Bezbolestné náhodné diferenciální soukromí se vzorkováním citlivosti. In 34th International Conference on Machine Learning (ICML’2017) , 2017.
Cynthia Dwork a Aaron Roth. Algoritmické základy diferenciálního soukromí . Now Publ. 2014.
Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan Mcmahan, Ilya Mironov, Kunal Talwar a Li Zhang. Hluboké učení s diferenciálním soukromím. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security – CCS16 , 2016.
Frank D. McSherry. Integrované dotazy na ochranu soukromí: An extensible platform for privacy-preserving data analysis. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data , SIGMOD ’09, strany 19-30, New York, NY, USA, 2009. ACM.
Přispěvatelé: Wikipedia. Hluboké učení, srpen 2018.
Leave a Reply