Helmholtzova rezonance
- Analýza Helmholtzovy rezonance
- Rezonance, impedance, fázová a frekvenční závislost
- Komplikace zahrnující délku
- Helmholtzovy rezonance a kytary
Analýza Helmholtzovy rezonance
Nyní se věnujme kvantitativním otázkám: Nejprve budeme předpokládat, že vlnová délka produkovaného zvuku je mnohem delší než rozměry rezonátoru. U lahví v animaci v horní části této stránky jsou vlnové délky 180 a 74 cm, takže tato aproximace je docela dobrá, ale vyplatí se ji ověřit vždy, když začnete něco popisovat jako Helmholtzův oscilátor. Důsledkem této aproximace je, že můžeme zanedbat změny tlaku uvnitř objemu nádoby: oscilace tlaku bude mít všude uvnitř nádoby stejnou fázi.
Nechť vzduch v hrdle má efektivní délku L a plochu průřezu S. Jeho hmotnost je pak SL krát hustota vzduchu ρ. (Některé komplikace ohledně efektivní délky jsou diskutovány na konci této stránky). Sestoupí-li tato „zátka“ vzduchu o malou vzdálenost x do láhve, stlačí vzduch v nádobě tak, že vzduch, který dříve zaujímal objem V, má nyní objem V – Sx. V důsledku toho se tlak tohoto vzduchu zvýší z atmosférického tlaku PA na vyšší hodnotu PA + p.
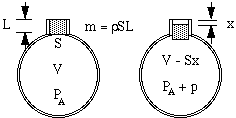
Nyní si možná myslíte, že zvýšení tlaku bude právě úměrné zmenšení objemu. Tak by tomu bylo, kdyby stlačování probíhalo tak pomalu, že by se teplota neměnila. Při kmitání, při kterém vzniká zvuk, jsou však změny rychlé, a tak teplota při stlačení stoupá, čímž dochází k větší změně tlaku. Technicky vzato jsou adiabatické, což znamená, že teplo nemá čas se pohybovat, a výsledná rovnice zahrnuje konstantu γ, poměr měrných tepel, který je pro vzduch přibližně 1,4. (To je vysvětleno v dodatku.) Výsledkem je, že změna tlaku p vyvolaná malou změnou objemu ΔV je právě
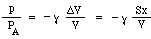
Nyní se hmotnost m pohybuje rozdílem tlaku mezi horní a dolní částí hrdla, tj. čistou silou pS, takže pro zrychlení a píšeme Newtonův zákon:
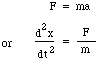
náhradou za F a m dostaneme: 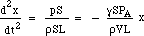
Takže obnovovací síla je úměrná posunutí. To je podmínka pro jednoduchý harmonický pohyb a ten má frekvenci, která je 1/2π násobkem druhé odmocniny konstanty úměrnosti, takže
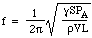
Nyní je rychlost c zvuku ve vzduchu určena hustotou, tlakem a poměrem měrných tepel, takže můžeme psát:
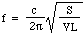
Dosadíme si pár čísel: pro litrovou láhev, jejíž S = 3 centimetry čtvereční a L = 5 centimetrů, je frekvence 130 Hz, což je přibližně C pod středním C. (Viz poznámky.) Vlnová délka je tedy 2,6 metru, což je mnohem více než láhev. To post hoc ospravedlňuje předpoklad vyslovený na začátku odvození.
Resonance, impedance, fázová a frekvenční závislost
Tuto část lze číst samostatně, ale pokud chcete podrobnější podklady, podívejte se na kapitoly Kmitání, Nucené kmitání a Akustická poddajnost, inertnost a impedance.
Vraťme se k mechanickému zobrazení a podívejme se na Helmholtzův rezonátor zvenčí, jak je znázorněno na prvním schématu: tlačíme kmitavou silou F s frekvencí f ,hmotu m (vzduch v hrdle rezonátoru), která je opřena o pružinu (uzavřený vzduch) s pružinovou konstantou k, jejíž druhý konec je pevný (vzduch v rezonátoru nemůže uniknout). Nerealisticky zanedbáme gravitaci a tření (prozatím).
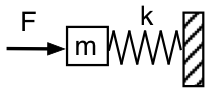
Síla potřebná k urychlení hmoty je úměrná zrychlení, a tedy úměrná f2. Při dostatečně nízké frekvenci je síla potřebná k urychlení hmoty zanedbatelná, takže F musí pružinu pouze stlačit a roztáhnout. V této mezeře je tedy působící síla F = +kx. (Síla pružiny je -kx.) Mechanická impedance soustavy při této nízké frekvenci je poddajná neboli pružinová. Akusticky to vypadá jako akustická poddajnost: tlačíme hmotu vzduchu v krčku a stlačujeme vzduch v rezonátoru. Působící síla F vpravo je ve fázi s x měřeným vpravo, takže je 90° za rychlostí a působící tlak je 90° za akustickým tokem do rezonátoru.
Pamatujte, že f2 závisí na zrychlení. Při dostatečně vysoké frekvenci je tedy síla pružiny zanedbatelná ve srovnání se silou urychlující hmotu. F je tedy ve fázi se zrychlením, což ji staví 90° před rychlost. Akusticky je působící tlak 90° před akustickým tokem do rezonátoru. Jedná se o mechanickou nebo akustickou setrvačnost.
Na rezonanční frekvenci (stále mluvíme o výše uvedeném náčrtu) může být amplituda velká při velmi malé síle. V rezonanci je tedy impedance velmi malá, pokud se na ni díváme z pohledu síly působící na hmotu zvenčí (nákres výše). Při rezonanci dochází k maximálnímu proudění do rezonátoru a z něj.
Nyní uvažujme, co se stane, když se podíváme na tlak uvnitř rezonátoru (směrem od hrdla). Zde se díváme na sílu působící na pružinu, takže naše mechanická analogie vypadá podle tohoto schématu.
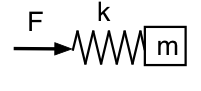
Tentokrát nízká frekvence znamená, že síla může být pro danou amplitudu malá: pružina a hmota se pohybují společně jako hmota a soustava tentokrát vypadá při nízké frekvenci inertivně. Při vysoké frekvenci se hmota téměř nepohybuje a systém vypadá jako pružina nebo poddajný. Fázové vztahy jsou tedy opačné než dříve: při nízké f vede p před U o 90°; při vysoké f p zaostává za U o 90°.
Výpočty zahrnující efektivní délku
Na prvním obrázku na této straně je „zátka“ vzduchu nakreslena, jako by to byl válec, který úhledně končí na obou koncích hrdla láhve. To je příliš zjednodušené. V praxi se se vzduchem v hrdle pohybuje další objem uvnitř i vně – jak naznačuje animace výše. Délka navíc, kterou je třeba přičíst ke geometrické délce hrdla, je obvykle (a velmi přibližně) 0,6násobek poloměru na vnějším konci a jeden poloměr na vnitřním konci).
|
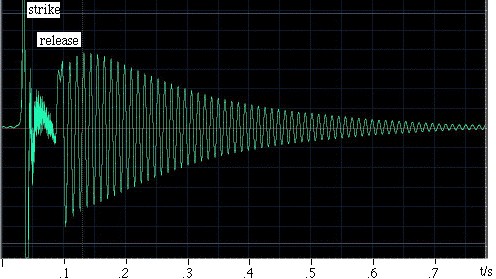
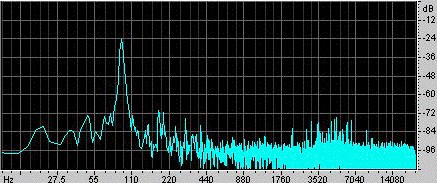
Příklad. Tento příklad vytvořil Ra Inta. Vzal kulový Helmholtzův rezonátor o objemu 0,00292 m3 s válcovým hrdlem o délce 0,080 m a ploše průřezu 0,00083 m2. Aby jej vyburcoval, udeřil do něj dlaní a poté jej uvolnil. Mikrofon uvnitř rezonátoru zaznamenává zvuk, který je znázorněn na oscilogramu vlevo. Je vidět, že ruka utěsňuje rezonátor po dobu spíše kratší než 0,1 s a že během této doby jsou kmity slabší a mají poměrně vysokou frekvenci. Po uvolnění ruky se vytvoří oscilace, které postupně odeznívají, protože ztrácejí energii vlivem viskózního a turbulentního odporu a také vyzařováním zvuku. Podrobné zkoumání ukazuje, že frekvence mírně stoupá, jak se ruka vzdaluje od otevřeného konce, protože tím ruka omezuje pevný úhel dostupný pro vyzařování a zvyšuje tak koncový efekt (nebo koncovou korekci). Délka hrdla se zvětší o jeden přepážkový a jeden nepřepážkový koncový efekt, takže jeho efektivní délka je 0,105 m. Při rychlosti zvuku 343 m/s dává výše uvedený výraz rezonanční frekvenci 90 Hz. |
|
Helmholtzovy rezonance a kytary
* Výše jsem uvedl, že vzduch v těle kytary se chová téměř jako Helmholtzův oscilátor. Tento případ je komplikovaný, protože tělo se může trochu nafouknout, když v něm stoupne tlak vzduchu – a také proto, že vzduch „v“ rezonančním otvoru kytary má geometrii, kterou si lze hůře představit než vzduch v hrdle láhve. V případě těla kytary je totiž délka zátky vzduchu přibližně stejná jako dva „koncové efekty“ na konci „trubky“, která je tlustá jen několik mm. Koncové efekty však souvisejí s poloměrem otvoru a mají podobnou velikost, takže hmotnost vzduchu je značná. Délka koncového efektu válcové trubky, která ústí do nekonečné rovinné přepážky, je 0,85násobkem poloměru trubky. Ačkoli ozvučná deska kytary není nekonečná, lze očekávat podobný koncový efekt, a tak by efektivní délka „zátky“ vzduchu byla přibližně 1,7násobkem poloměru otvoru. (Někteří výrobci tuto hodnotu zvyšují tím, že pod rezonanční otvor připevní krátkou trubku o stejném poloměru).
Několik lidí napsalo dotaz, jak velký by měl být rezonanční otvor pro daný nástroj. Na tuto otázku můžeme začít odpovídat pomocí výše uvedené rovnice. Důležité je však bobtnání těla. Díky tomu je „pružení“ vzduchu spíše měkčí, a tím se snižuje frekvence. Čistě Helmholtzovu rezonanci lze zkoumat při zachování konstantního objemu těla. Při měření se běžně používá zahrabání kytary do písku, aby se znemožnilo bobtnání nebo „dýchání“ těla. Na kytary se však v této situaci obvykle nehraje. Helmholtzův výpočet tak u skutečného pružného těla poskytne nadhodnocenou rezonanční frekvenci.
Předpokládejme kruhový rezonanční otvor o poloměru r, takže S = πr2 a L = 1,7r, jak bylo vysvětleno výše. Když dosadíme do rovnice pro Helmholtzovu frekvenci pomocí c = 340 m/s, dostaneme:
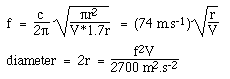
Všimněte si, že používáme standardní jednotky SI: použili jsme rychlost zvuku v metrech a sekundách, takže objem musí být v metrech krychlových a frekvence v hertzech, abychom dostali odpověď v metrech.
Je to složitější, když tónové otvory nejsou kruhové, protože konečný efekt se nerovná efektu kruhu o stejné ploše. Doktorand a loutnista John McLennan o tom sepisuje zprávu o některých měřeních, kterou zde brzy zveřejníme.
U nástrojů z rodiny kytar a houslí je Helmholtzova rezonance (plus rezonance těla) často blízko frekvence druhé nejnižší struny nebo o něco níže, tedy kolem D u houslí nebo G-A u kytary. Helmholtzovu frekvenci můžete podstatně snížit nebo posunout zakrytím celého otvoru nebo jeho části vhodně tvarovaným kusem tuhého kartonu. Pokud pak zahrajete tón v blízkosti rezonance a poté posunete karton tak, aby střídavě zakrýval a odhaloval otvor, jasně uslyšíte účinek rezonance.
Je efekt 0,85r rozumný? Ra Inta, který v naší laboratoři dělal doktorát o kytarové akustice, navrhuje zajímavou demonstraci:
Vlhčete struny na kytaře, aby nevibrovaly (např. kapesník mezi strunami a hmatníkem). Držte dlaň jedné ruky nad ozvučným otvorem a v jeho blízkosti. Prstem druhé ruky udeřte prudce do ozvučné desky v blízkosti ozvučného otvoru a blízko 1. struny. Na dlani ucítíte pulsování vzduchu. Úder vašeho prstu zatlačí rezonanční desku dovnitř a vytlačí část vzduchu z těla. Nyní postupně oddalujte ruku od otvoru a pokračujte v úderech prstem. Kdy přestanete cítit pohyb vzduchu? Tím získáte přibližný odhad délky „koncového efektu“ v případě rezonančního otvoru.
Nastavení Helmholtzovy rezonance
Mezi publikacemi Johna McLennana, doktoranda této laboratoře, je článek, ve kterém mění Helmholtzovu rezonanci pomocí změny rychlosti zvuku.
- McLennan, J.E. (2003) „Studie A0 a A1 na houslích s použitím směsí CO2, He a vzduchu a helia“. Acustica, 89, 176-180.
Několik obrázků historických Helmholtzových rezonátorů poskytl Thomas B. Greenslade, Kenyon College, Ohio.
Leave a Reply