Greenova funkce

Všeobecně řečeno, Greenova funkce je integrální jádro, které lze použít k řešení diferenciálních rovnic z velkého počtu rodin, včetně jednodušších příkladů, jako jsou obyčejné diferenciální rovnice s počátečními nebo okrajovými podmínkami, i složitějších příkladů, jako jsou nehomogenní parciální diferenciální rovnice (PDE) s okrajovými podmínkami. Greenovy funkce, které jsou důležité z řady důvodů, umožňují názornou interpretaci dějů spojených se zdrojem síly nebo s nábojem soustředěným v bodě (Qin 2014), a jsou tak obzvláště užitečné v oblastech aplikované matematiky. Konkrétně jsou metody Greenových funkcí hojně využívány např, fyzice a inženýrství.

Přesněji řečeno, je dán lineární diferenciální operátor působící na kolekci rozdělení nad podmnožinou nějakého euklidovského prostoru , Greenova funkce v bodě odpovídajícím je libovolné řešení

(1)

kde označuje delta funkci. Motivace pro definici takové funkce je široká, ale vynásobením výše uvedené identity funkcí a integrací vzhledem k dostaneme

(2)

Pravá strana se díky vlastnostem delta funkce redukuje pouze na , a protože je lineární operátor působící pouze na a ne na , lze levou stranu přepsat jako

(3)

Tato redukce je užitečná zejména při řešení v diferenciálních rovnicích tvaru

(4)

kde výše uvedená aritmetika potvrzuje, že

(5)

a z čehož vyplývá, že má konkrétní integrální tvar

(6)

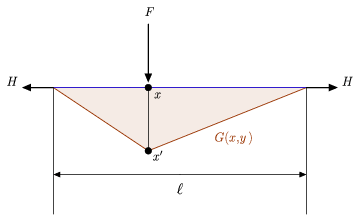
Výše uvedený obrázek ilustruje jak intuitivní fyzikální interpretaci Greenovy funkce, tak i relativně jednoduchou přidruženou diferenciální rovnici, se kterou lze výše uvedenou definici porovnat (Hartmann 2013). Konkrétně je na něm znázorněno napnuté lano délky zavěšené mezi dvěma stěnami, které je drženo na místě stejnou vodorovnou silou působící na každém z jeho konců, a boční zatížení umístěné v nějakém vnitřním bodě na laně. Nechť je bod odpovídající na vychýleném laně, předpokládejme, že dolů působící síla je konstantní, řekněme , a nechť označuje výchylku lana. Této fyzikální soustavě odpovídá diferenciální rovnice

(7)

pro s , systém, jehož jednoduchost umožňuje explicitní zápis jak jeho řešení , tak jeho Greenovy funkce :

(8)

a

(9)

resp. Jak ukazuje výše uvedený obrázek, posunuté lano má po částech lineární tvar daný výše uvedeným vztahem , čímž se potvrzuje tvrzení, že Greenova funkce přiřazená této soustavě představuje působení vodorovného lana odpovídající působení síly .

Greenova funkce, která bere dvojici argumentů , se někdy označuje jako dvoubodová Greenova funkce. To je rozdíl od vícebodových Greenových funkcí, které mají význam zejména v oblasti teorie mnoha těles.

Jako elementární příklad dvoubodové funkce definované výše uvažujme problém určení potenciálu generovaného rozložením náboje, jehož hustota náboje je , přičemž aplikace Poissonovy rovnice a Coulombova zákona na potenciál při vytvořený každým prvkem náboje dává řešení

(10)

což platí, za určitých podmínek v oblasti, kde . Protože na pravou stranu lze pohlížet jako na integrální operátor převádějící na , lze toto řešení přepsat v termínech Greenovy funkce mající tvar

(11)

kde lze řešení přepsat:

(12)

(Arfken 2012).

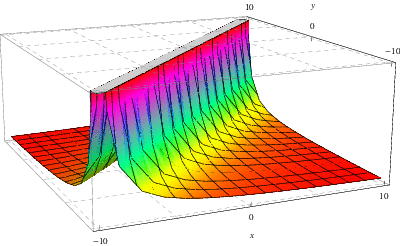
Výše uvedený obrázek ukazuje Greenovu funkci spojenou s řešením výše diskutované rovnice –, kde zde, a , respektive , je vynesena na ose -, respektive -.

Někdy vyčerpávající seznam Greenových funkcí odpovídajících různým diferenciálním rovnicím vede na internetu Kevin Cole (Cole 2000).

Vzhledem k množství literatury napsané o Greenových funkcích může vzniknout několik různých zápisů a definic, z nichž některé se aktuálně liší od výše uvedených, ale které obecně nemají vliv na důležité vlastnosti výsledků. Jak ukazuje výše uvedený příklad, někteří autoři například dávají přednost označování proměnných a pomocí vektorů a , aby zdůraznili skutečnost, že jde o prvky pro některé , které mohou být větší než 1 (Arfken 1985). Poměrně často se také setkáváme s definicí se záporným znaménkem, takže je definována funkce, pro kterou

(13)

ale vzhledem k tomu, že tato čistě fyzikální úvaha nemá žádný vliv na základní matematiku, je toto hledisko obvykle přehlíženo. Je známo i několik dalších zápisů Greenovy funkce, z nichž některé zahrnují použití malého písmene namísto (Stakgold 1979), stejně jako zařazení svislé čáry namísto čárky, např, (Duffy 2001).

V jiných případech literatura uvádí definice, které jsou úzce spjaty s kontexty, v nichž jsou prezentovány. Někteří autoři například definují Greenovy funkce jako funkce, které splňují určitý soubor podmínek, např. existenci na zvláštním druhu oboru, spojení s velmi konkrétním diferenciálním operátorem nebo splnění přesného souboru okrajových podmínek. Jeden z nejčastějších takových příkladů lze nalézt v poznámkách např, Specka, kde je Greenova funkce definována tak, aby splňovala pro body a pro všechny body ležící na hranici z (Speck 2011). Tato konkrétní definice představuje integrální jádro odpovídající řešení zobecněné Poissonovy rovnice, a proto by při adaptaci na obecnější prostředí narazila na zjevná omezení. Na druhou stranu takové příklady nejsou bez výhod. Například v případě výše uvedeného zobecněného Poissonova příkladu lze každou takovou Greenovu funkci rozdělit tak, že

(14)

kde a pro regulární Laplacián (Hartman 2013). V takových situacích se označuje jako fundamentální řešení základní diferenciální rovnice a jako její regulární řešení; a se proto někdy nazývají fundamentální, resp. regulární část .

Několik základních vlastností obecné Greenovy funkce vyplývá bezprostředně (nebo téměř bezprostředně) z její definice a přenáší se na všechny konkrétní případy. Například pokud je jádro operátoru netriviální, pak může být s jedním operátorem spojeno několik Greenových funkcí; v důsledku toho je třeba projevit opatrnost, když se mluví o „této“ Greenově funkci. Greenovy funkce splňují ve svých dvou argumentech adjungovanou symetrii, takže

(15)

kde je zde definováno jako řešení rovnice

(16)

Zde platí, že je adjunktem . Jedním z bezprostředních důsledků tohoto faktu je, že pro samoadjungované operátory je symetrický:

(17)

Tato identita se často nazývá princip reciprocity a fyzikálně říká, že odezva na způsobená jednotkovým zdrojem na je stejná jako odezva na způsobená jednotkovou silou na (Stakgold 1979).

Základní vlastností každé Greenovy funkce je, že poskytuje způsob, jak popsat odezvu řešení libovolné diferenciální rovnice na nějaký druh zdrojového členu za přítomnosti určitého počtu okrajových podmínek (Arfken et al. 2012). Někteří autoři se domnívají, že Greenova funkce plní v teorii parciálních diferenciálních rovnic zhruba analogickou úlohu jako Fourierovy řady při řešení obyčejných diferenciálních rovnic (Mikula a Kos 2006).

Pro abstraktnější scénáře existuje řada pojmů, které slouží jako kontextově specifické analogie pojmu Greenova funkce. Například ve funkcionální analýze je často užitečné uvažovat o tzv. zobecněné Greenově funkci, která má mnoho analogických vlastností při abstraktní integraci vůči funkcionálům, nikoliv funkcím. Taková zobecnění skutečně přinesla zcela analogické odvětví teoretické analýzy PDE a sama jsou předmětem velkého množství výzkumů.

.