Articles /

Gram-Schmidtův proces

podle Marco Taboga, PhD

Gram-Schmidtův proces (nebo postup) je posloupnost operací, které umožňují transformovat množinu lineárně nezávislých vektorů na množinu ortonormálních vektorů, které pokrývají stejný prostor, jaký pokrývá původní množina.

Obsah

Předpoklady

Zopakujme si některé pojmy, které jsou nezbytné pro pochopení Gram-Schmidtova procesu.

Připomeňme si, že o dvou vektorech $r$ a $s$ říkáme, že jsou ortogonální tehdy a jen tehdy, když je jejich vnitřní součin roven nule, to znamená,

Při daném vnitřním součinu můžeme definovat normu (délku) vektoru $s$ takto:

Množina vektorů se nazývá ortonormální tehdy a jen tehdy, když její prvky mají jednotkovou normu a jsou navzájem ortogonální. Jinými slovy, množina K vektorů je ortonormální tehdy a jen tehdy, když

Dokázali jsme, že vektory ortonormální množiny jsou lineárně nezávislé.

Je-li báze vektorového prostoru zároveň ortonormální množinou, nazývá se ortonormální báze.

Projekce na ortonormální množiny

Při Gramově-Schmidtově postupu opakovaně používáme následující větu, která ukazuje, že každý vektor lze rozložit na dvě části: 1) jeho projekci na ortonormální množinu a 2) reziduum, které je ortogonální k dané ortonormální množině.

Věta Nechť $S$ je vektorový prostor vybavený vnitřním součinem . Nechť je ortonormální množina. Pro libovolný $sin S$ mámekde $arepsilon _{S}$ je ortogonální k $u_{k}$ pro libovolné $k=1,ldots ,K.$

Důkaz

DefinicePak pro každé $j=1,ldots ,K$ máme, žekde: v krocích $rame{A}$ a $rame{B}$ jsme využili toho, že vnitřní součin je lineární ve svém prvním argumentu; v kroku $rame{C}$ jsme použili fakt, že pokud $keq j$, protože máme co do činění s ortonormální množinou; v kroku $rame{D}$ jsme použili fakt, že norma $u_{j}$ je rovna 1. Proto je $arepsilon _{S}$, jak je definován výše, ortogonální ke všem prvkům ortonormální množiny, což dokazuje větu.

Výraz se nazývá lineární projekce $s$ na ortonormální množinu , zatímco výraz $arepsilon _{S}$ se nazývá reziduum lineární projekce.

Normalizace

Dalším snad zřejmým faktem, který budeme v Gram-Schmidtově postupu opakovaně používat, je, že vezmeme-li libovolný nenulový vektor a vydělíme jej jeho normou, pak výsledkem dělení je nový vektor, který má jednotkovou normu.

Jinými slovy, jestliže , pak podle vlastnosti definičnosti normy máme, že

V důsledku toho můžeme definovata podle pozitivity a absolutní homogenity normy, máme

Přehled postupu

Nyní, když víme, jak normalizovat vektor a jak jej rozložit na projekci na ortonormální množinu a reziduum, jsme připraveni vysvětlit Gramův-Schmidtův postup.

Uvedeme přehled postupu, poté jej vyjádříme formálně jako větu a všechny technické detaily probereme v důkazu věty.

Zde je přehled.

Máme danou množinu lineárně nezávislých vektorů .

Na začátku procesu normalizujeme první vektor, tj. definujeme

Ve druhém kroku promítneme $s_{2}$ na $u_{1}$:kde $arepsilon _{2}$ je reziduum projekce.

Poté reziduum normalizujeme:

Později dokážeme, že (aby bylo možné provést normalizaci), protože výchozí vektory jsou lineárně nezávislé.

Takto získané dva vektory $u_{1}$ a $u_{2}$ jsou ortonormální.

Ve třetím kroku promítneme $s_{3}$ na $u_{1}$ a $u_{2}$: a vypočítáme reziduum projekce $arepsilon _{3}$.

Poté jej normalizujeme:

Takto postupujeme, dokud nedostaneme poslední normalizované reziduum $u_{K}$.

Na konci procesu tvoří vektory ortonormální množinu, protože:

  1. jsou výsledkem normalizace, a v důsledku toho mají jednotkovou normu;

  2. každý $u_{k}$ je získán z rezidua, které má vlastnost být ortogonální k .

Pro doplnění tohoto přehledu připomeňme, že lineární rozpětí je množina všech vektorů, které lze zapsat jako lineární kombinace ; označujeme jia je to lineární prostor.

Protože vektory jsou lineárně nezávislé kombinace , lze každý vektor, který lze zapsat jako lineární kombinaci , zapsat také jako lineární kombinaci . Proto se rozpětí obou množin vektorů shodují:

Formální tvrzení

Gramův-Schmidtův postup zde formalizujeme jako větu, jejíž důkaz obsahuje všechny technické podrobnosti postupu.

Věta Nechť $S$ je vektorový prostor vybavený vnitřním součinem . Nechť jsou lineárně nezávislé vektory. Pak existuje množina ortonormálních vektorů taková, žepro libovolný $kleq K$.

Důkaz

Důkaz provedeme indukcí: nejprve dokážeme, že věta platí pro $k=1$, a pak dokážeme, že platí pro obecný k, jestliže platí pro $k-1$. Když $k=1$, má vektor jednotkovou normu a sám o sobě tvoří ortonormální množinu: žádné jiné vektory neexistují, takže podmínka ortogonality je triviálně splněna. Množina je množina všech skalárních násobků $s_{1}$, které jsou zároveň skalárními násobky $u_{1}$ (a naopak). Proto Nyní předpokládejme, že věta je pravdivá pro $k-1$. Pak můžeme promítnout $s_{k}$ na :kde reziduum $arepsilon _{k}$ je ortogonální k . Předpokládejme, že $arepsilon _{k}=0$. Pak,protože podle předpokladu pro libovolný $jleq k-1$, máme, že pro libovolný $jleq k-1$, kde $lfa _{jl}$ jsou skaláry. Proto,jinými slovy, předpoklad, že $arepsilon _{k}=0$ vede k závěru, že $s_{k}$ je lineární kombinací . To však není možné, protože jedním z předpokladů věty je, že jsou lineárně nezávislé. V důsledku toho musí platit, že . Můžeme tedy reziduum normalizovat a definovat vektor, který má jednotkovou normu. Již víme, že $arepsilon _{k}$ je ortogonální k . Z toho vyplývá, že také $u_{k}$ je ortogonální k . Tedy je ortonormální množina. Nyní vezměme libovolný vektor $sin S$, který lze zapsat jakokde jsou skaláry. Protože podle předpokladu máme, že rovnici (2) lze zapsat také jako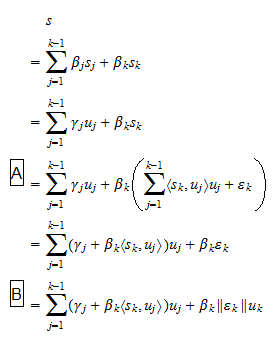kde jsou skaláry, a: v kroku $rame{A}$ jsme použili rovnici (1); v kroku $rame{B}$ jsme použili definici $u_{k}$. Tím jsme dokázali, že každý vektor, který lze zapsat jako lineární kombinaci , lze také zapsat jako lineární kombinaci . Předpoklad (3) umožňuje zcela analogicky dokázat i obrácený důkaz: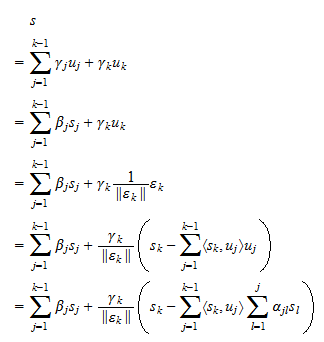Jinými slovy, každá lineární kombinace je také lineární kombinací . To dokazuje, že a uzavírá důkaz.

Každý prostor vnitřního součinu má ortonormální bázi

Následující věta představuje důležitý důsledek Gram-Schmidtova procesu.

Věta Nechť $S$ je vektorový prostor vybavený vnitřním součinem . Jestliže $S$ má konečnou dimenzi , pak pro $S$ existuje ortonormální báze .

Důkaz

Protože $S$ má konečnou dimenzi, existuje pro $S$ alespoň jedna báze tvořená K vektory . Na tuto bázi můžeme aplikovat Gram-Schmidtův postup a získat ortonormální množinu . Protože je báze, zahrnuje $S$. Proto 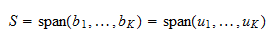Takže je ortonormální báze $S$.

Řešená cvičení

Níže najdete několik cvičení s vysvětleným řešením.

Cvičení 1

Uvažujme prostor $S$ všech $3imes 1$ vektorů s reálnými položkami a vnitřním součinem kde $r,sin S$ a $s^{op }$ je transpozice $s$. Definujte vektor

Normalizujte $s$.

Řešení

Norma $s$ jeTakže, normalizace $s$ je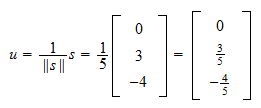

Cvičení 2

Uvažujme prostor $S$ všech $2imes 1$ vektorů s reálnými položkami a vnitřním součinemkde $r,sin S$ . Uvažujme dva lineárně nezávislé vektory

Transformujte je do ortonormální množiny pomocí Gram-Schmidtova postupu.

Řešení

Norma $s_{1}$ je Tedy, první ortonormální vektor jeVnitřní součin $s_{2}$ a $u_{1}$ je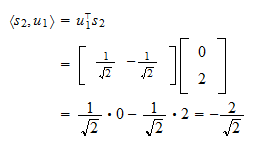Projekce $s_{2}$ na $u_{1}$ je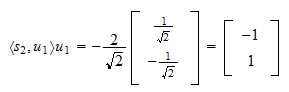Reziduál projekce je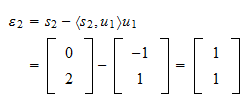Norma reziduálu jea normovaný reziduál jeTakže, ortonormální množina, kterou jsme hledali, je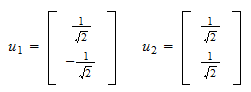

Jak citovat

Citujte prosím jako:

Taboga, Marco (2017). „Gram-Schmidtův proces“, Přednášky z maticové algebry. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.

Leave a Reply