Gibbsovo vzorkování

Stejně jako ostatní metody MCMC, Gibbsův vzorkovač konstruuje Markovův řetězec, jehož hodnoty konvergují k cílovému rozdělení. Gibbsovo vzorkování je vlastně specifickým případem Metropolisova-Hastingsova algoritmu, v němž jsou návrhy vždy přijaty.

Pro upřesnění předpokládejme, že chcete vzorkovat vícerozměrné rozdělení pravděpodobnosti.

Poznámka: Vícerozměrné rozdělení pravděpodobnosti je funkce více proměnných (tj. Dvourozměrné normální rozdělení).

Nevíme, jak z něj přímo vzorkovat. Díky jisté matematické pohodlnosti nebo možná jen díky štěstí však náhodou známe podmíněné pravděpodobnosti.

Tady nastupuje Gibbsovo vzorkování. Gibbsovo vzorkování je použitelné v případech, kdy společné rozdělení není explicitně známo nebo je obtížné z něj přímo vzorkovat, ale podmíněné rozdělení jednotlivých proměnných je známo a je snazší z něj vzorkovat.

Začneme tím, že zvolíme počáteční hodnotu náhodné veličiny X & Y. Poté budeme vzorkovat z podmíněného rozdělení pravděpodobnosti X vzhledem k Y = Y⁰ označovaného p(X|Y⁰). V dalším kroku vybereme novou hodnotu Y podmíněnou X¹, kterou jsme právě vypočítali. Postup opakujeme pro dalších n – 1 iterací, přičemž střídavě vybíráme nový vzorek z podmíněného rozdělení pravděpodobnosti X a podmíněného rozdělení pravděpodobnosti Y vzhledem k aktuální hodnotě druhé náhodné veličiny.

Podívejme se na příklad. Předpokládejme, že máme následující posteriorní a podmíněné rozdělení pravděpodobnosti.

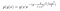
kde g(y) obsahuje členy, které neobsahují x, a g(x) obsahuje ty, které nezávisí na y.

Neznáme hodnotu C (normalizační konstanty). Známe však podmíněná rozdělení pravděpodobnosti. Proto můžeme k aproximaci posteriorního rozdělení použít Gibbsovo vzorkování.

Poznámka: Podmíněné pravděpodobnosti jsou ve skutečnosti normální rozdělení a lze je přepsat takto:

Díky předchozím rovnicím přistoupíme k implementaci algoritmu Gibbsova vzorkování v jazyce Python. Na začátku importujeme následující knihovny.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

Definujeme funkci pro posteriorní rozdělení (předpokládáme C=1).

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

Poté vykreslíme rozdělení pravděpodobnosti.

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Nyní se pokusíme odhadnout pravděpodobnostní rozdělení pomocí Gibbsova vzorkování. Jak jsme se již zmínili, podmíněné pravděpodobnosti jsou normální rozdělení. Proto je můžeme vyjádřit v termínech mu a sigma.

V následujícím bloku kódu definujeme funkce pro mu a sigma, inicializujeme naše náhodné veličiny X & Y a nastavíme N (počet iterací).

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

Projdeme postupně algoritmem Gibbsova vzorkování.

for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x

Nakonec vykreslíme výsledky.

plt.hist(x, bins=50);
plt.hist(y, bins=50);

plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

Jak je vidět, pravděpodobnostní rozdělení získané pomocí Gibbsova vzorkovacího algoritmu dobře aproximuje cílové rozdělení.

Závěr

Gibbsovo vzorkování je metoda Monte Carlo s Markovovým řetězcem, která iterativně vybírá instance z rozdělení každé proměnné, podmíněné aktuálními hodnotami ostatních proměnných, za účelem odhadu složitých společných rozdělení. Na rozdíl od Metropolisova-Hastingsova algoritmu vždy přijímáme návrh. Gibbsovo vzorkování tak může být mnohem efektivnější.